Основные свойства б.М. Последовательностей.

Свойство 1. Алгебраическая сумма конечного числа б.м. последовательностей есть б.м. последовательность.

Доказательство. (Докажем для суммы 3-х б.м. величин. В др. случаях доказательство аналогично).

Пусть _n,_n,_n – б.м. последовательности при n→. Докажем, что (_n+_n+_n) – также б.м. последовательность.

Возьмем произвольное сколь угодно малое число >0.

По условию _n – б.м. последовательность. Следовательно, по числу можно указать номерN₁ такой, что все значения _n, у которых номер n>N₁, удовлетворяют неравенству .

Так как _n и _n – б.м. последовательности, то по тому же числу можно указать номераN₂ и N₃ такие, что приn>N₂ и 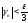приn>N₃.

Положим N=max{N₁,N₂,N₃}. Тогда при n>N будут выполняться все 3 неравенства. Тогда , т.е. (_n+_n+_n) – б.м. ч.т.д.

Свойство 2. Произведение ограниченной последовательности х_n на бесконечно малую последовательность _n - есть б.м. последовательность.

Доказательство. По условию х_n – ограниченная, т.е.

Возьмем >0 – сколь угодно малое. Т.к. _n - б.м., то .

Т.к. 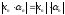,то при n>N будет 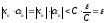, т.е. х_n _n -б.м. ч.т.д.

Лемма. Если все члены последовательности {x_n} отличны от 0 и если x_n→а, n→, где а≠0, то - ограниченная последовательность.

Доказательство. Т.к. а≠0, то

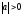
Положим =. Т.к.=а,то взятому отвечает номер

Имеем

Тогда при n>N будет , а значит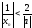

Положим С=

Тогда при всех nN , т.е.- ограниченная последовательность. Ч.т.д.

Свойство 3. Пусть _n - есть б.м. последовательность при n→. Пусть все члены последовательности {x_n} отличны от 0 и x_n→a, n→, где a≠0. Тогда - б.м. последовательность.

Доказательство. По лемме последовательность - ограниченная.

Имеем =_n, т.е. - представляет собой произведение ограниченной последовательности на б.м. Тогда по свойству 2 -- б.м. ч.т.д.

Бесконечно большие последовательности (величины).

Определение. Последовательность {х_n}, пробегающая последовательность значений х₁,х₂,….,х_n,.., называется бесконечно большой последовательностью, если для любого положительного числа М (каким бы большим мы его ни взяли) можно указать номер N такой, что все значения x_n, у которых номер n>N, удовлетворяют неравенству

(1)

Тот факт, что {х_n} бесконечно-большая (б.б.) последовательность при n→, выражают также словами «последовательность {х_n} стремиться к »:

(2)

Из неравенства (1) следует, что вместе с х_n бесконечно большими будут также последовательности -х_n и х_n.

Расширение понятие предела.

- и + - несобственные числа.

Определение 1. x_n→+ при n→, если

(последовательность неограниченна сверху).

Определение 2. x_n→- при n→, если

(последовательность неограниченна снизу).

Пример 1. Пусть {x_n}={n}={1,2,…,n,…}. Какое бы число M>0 мы ни взяли, переменная x_n при возрастании n «перерастет» М, т.е. для всех n, начиная с некоторого, будет . Следовательно, переменнаяx_n=n – б.б. при n→ и.

Пример 2. Пусть {x_n}={-n}={-1,-2,…,-n,…}. Какое бы число M>0 мы ни взяли,. для всех n, начиная с некоторого, будет . Следовательно, переменнаяx_n= -n – б.б. при n→ и .

Пример 3. Пусть {x_n}={(-1)ⁿn}={-1,2,-3,…}. Имеем 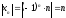. Следовательно, какое бы числоM>0 мы ни взяли, для всех n, начиная с некоторого, будет . Следовательно, переменнаяx_n=(-1)ⁿn – б.б. при n→ и .

Пример 4. Покажем, что если q>1, то qⁿ – бесконечно большая при n→.

Возьмем любое сколь угодно большое число М>0 и рассмотрим неравенство qⁿ>M (*)

Имеем qⁿ>M qⁿ>M  (т.к.q>1, то )

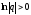Если теперь в качестве N взять N=, тогда приn>N окажется, чтоqⁿ>М.

А это означает, что х_n=qⁿ – бесконечно большая при q>1.