
- •Свойства прообразов и образов
- •Обратная функция.
- •Примеры
- •Эквивалентные определения
- •Примеры
- •Примеры
- •Суперпозиция функций (сложная функция).
- •Определение
- •Свойства композиции
- •Дополнительные свойства
- •Счетные и несчетные множества.
- •Свойства отношения равномощности.
- •Свойство полноты множества вещественных чисел.
- •Плотность множества рациональных чисел в r.
- •Промежутки числовой прямой.
- •Модуль числа.
- •Свойства модуля.
- •Ограниченные числовые множества. Границы числовых множеств.
- •Свойства точных границ.
- •Последовательности.
- •Числа x1,x2,…,xn – члены последовательности.
- •Лемма о вложенных отрезках. (Принцип Коши-Кантора)
- •Предел последовательности.
- •Свойства пределов числовых последовательностей.
- •Предел и алгебраические операции.
- •Предельный переход в неравенствах.
- •Бесконечно малые последовательности (величины).
- •Основные свойства б.М. Последовательностей.
- •Бесконечно большие последовательности (величины).
- •Расширение понятие предела.
- •Основные свойства бесконечно больших последовательностей.
- •Связь между бесконечно малыми и бесконечно большими последовательностями.
- •Арифметические свойства предела. (Бесконечно большие последовательности и арифметические операции)
- •Вопросы существования пределов.
- •Свойства фундаментальной последовательности.
- •Монотонные последовательности.
- •Число е.
- •Предел подпоследовательности сходящейся последовательности.
- •Вычисление пределов некоторых последовательностей.
Одна и та же по наименованию величина в одних условиях может быть постоянной, в других – переменной. Например, объем комнаты – величина постоянная, а объем резинового шарика во время наполнения его газом – переменная величина.
Переменная величина является отвлеченной или числовой переменной. Ее обозначают каким-либо символом (буквой), которому приписывают числовые значения.
Переменная считается заданной, если указано множество Х значений, которые она может принять.
Постоянную величину удобно рассматривать как частный случай переменной; он отвечает предположению, что множество Х состоит из одного элемента.
Определение функции.
Зависимая-независимая переменная…
Множество Х называется множеством задания функции, множество Y - множеством изменения функции.
Примеры. …
1) Функция
Дирихле,
2) y=sgn
x= (signum)
X=(-;+),Y={-1,0,1}
(signum)
X=(-;+),Y={-1,0,1}
3) у=[х] – целая часть от числа. у={x} – дробная часть числа.
Пусть дано отображение
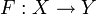 ,
и
,
и .
Тогдасуже́нием
функции F
на M
называется функция
.
Тогдасуже́нием
функции F
на M
называется функция
 ,
определяемая равенством
,
определяемая равенством
![]() .
.
Это определение подчеркивает, что фиксация области определения является частью определения функции.
Пусть
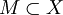 .
Тогдао́бразом
множества M
называется подмножество Y,
определяемое равенством
.
Тогдао́бразом
множества M
называется подмножество Y,
определяемое равенством
![]() .
.
Множество
![]() называетсяобразом
отображения
называетсяобразом
отображения
![]() и
обозначается
и
обозначается
![]() .
.
Пусть f:
X→Y.
Если х0 X,
то соответствующий ему элемент у0=f(x0)
X,
то соответствующий ему элемент у0=f(x0) Y
называется образом
х0
(при отображении f).
Y
называется образом
х0
(при отображении f).
Совокупность
всех элементов х X,
образом которых является данный элемент
у0
X,
образом которых является данный элемент
у0 В,
называется прообразом
(полным
прообразом)
элемента у0
(и обозначается
f-1(y0))
В,
называется прообразом
(полным
прообразом)
элемента у0
(и обозначается
f-1(y0))
Пусть задано отображение
 ,
,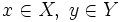 иy
= F(x).
Тогда x
называется проо́бразом
y,
а y
называется о́бразом
x.
Согласно определению отображения,
каждый элемент
иy
= F(x).
Тогда x
называется проо́бразом
y,
а y
называется о́бразом
x.
Согласно определению отображения,
каждый элемент
 должен
иметь ровно один образ, но элемент
должен
иметь ровно один образ, но элемент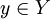 может
не иметь прообразов либо иметь один
или несколько.
может
не иметь прообразов либо иметь один
или несколько.Например, пусть дана функция
 ,
гдеF(x)
= x2.
Тогда
,
гдеF(x)
= x2.
Тогда
y = − 1 не имеет прообразов;
y = 0 имеет единственный прообраз x = 0;
y = 1 имеет два прообраза: x1 = 1 и x2 = − 1.
Пусть задано отображение
 ,
и
,
и .
Тогда множество
.
Тогда множество называетсяпо́лным
проо́бразом
элемента y.
Полный прообраз обозначается F
- 1(y).
называетсяпо́лным
проо́бразом
элемента y.
Полный прообраз обозначается F
- 1(y).
Например, пусть
 ,
иF(x)
= sinx.
Тогда
,
иF(x)
= sinx.
Тогда
![]() .
.
Пусть
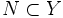 .
Тогдапроо́бразом
множества N
называется подмножество X,
определяемое равенством
.
Тогдапроо́бразом
множества N
называется подмножество X,
определяемое равенством
![]() .
.
Например, пусть
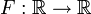 ,
иF(x)
= cosx.
Тогда
,
иF(x)
= cosx.
Тогда
![]() ,
,
 .
.
Свойства прообразов и образов
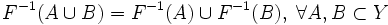 ;
;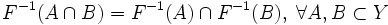 ;
; ;
; .
Заметим отсутствие равенства в этом
случае.
.
Заметим отсутствие равенства в этом
случае.
Обратная функция.
Определение. Пусть функция f:A→B.
1) Если для любых двух различных элементов х1 и х2 из А их образы у1=f(x1) и у2=f(x2) также различны,
х1≠х2
 f(x1)≠f(x2)
(f(x1)=f(x2)
f(x1)≠f(x2)
(f(x1)=f(x2)
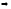 x1=x2).то
отображение f
называется инъекцией.
x1=x2).то
отображение f
называется инъекцией.
Отображение
![]() называетсяинъекцией
(или вложением,
или отображением
в Y),
если разные элементы множества
X
переводятся в разные элементы множества
Y.
Т.е. если х1х2f(x1)f(x2).
называетсяинъекцией
(или вложением,
или отображением
в Y),
если разные элементы множества
X
переводятся в разные элементы множества
Y.
Т.е. если х1х2f(x1)f(x2).
Формально это
значит, что если два образа совпадают,
то совпадают и прообразы (![]() ).
Инъективность является необходимым
условиембиективности
(достаточно вместе с сюръективностью).
).
Инъективность является необходимым
условиембиективности
(достаточно вместе с сюръективностью).
(Инъекцию можно
также определить как отображение, для
которого существует левое обратное,
т.е.
![]() инъективно,
если существует
инъективно,
если существует![]() такое,
что
такое,
что![]() .)
.)
Примеры
 —инъективно.
—инъективно.  —инъективно.
—инъективно.  —не является
инъективным (F(
- 2) = F(2)
= 4).
—не является
инъективным (F(
- 2) = F(2)
= 4).
2) Отображение
![]() называетсясюръективным
(или сюръекцией,
или отображением
на Y),
если каждый элемент
множества Y
является образом
хотя бы одного элемента множества X,
т. е.
называетсясюръективным
(или сюръекцией,
или отображением
на Y),
если каждый элемент
множества Y
является образом
хотя бы одного элемента множества X,
т. е.
![]() .
.
Т.е. если f(X)=Y
или
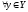
 такое, чтоy=f(x),
то отображение f
действует на
Y
(отображение «на»).Такое
отображение также называется сюръекцией.
такое, чтоy=f(x),
то отображение f
действует на
Y
(отображение «на»).Такое
отображение также называется сюръекцией.
В общем случае, т.е. когда f(X)Y, говорят, что f есть отображение X «в» Y.
|
|
Эквивалентные определения
Следующие свойства
отображения
![]() эквивалентны:
эквивалентны:
F сюръективно
каждый элемент множества Y имеет хотя бы один прообраз во множестве X при отображении F.
образ множества X при отображении F(X) совпадает с Y
F имеет правое обратное отображение, т.е. такое отображение
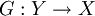 ,
чтоF(G(y))
= y
для любого
,
чтоF(G(y))
= y
для любого
 .
.
Примеры
 —сюръективно.
—сюръективно.  —сюръективно.
—сюръективно.  —не является
сюръективным.
—не является
сюръективным.
Отображение f которое одновременно является инъекцией и сюръекцией, называется биекцией или взаимно однозначным соответствием между А и В.
В этом случае множества А и В находятся во взаимно однозначном соответствии.

Функция
![]() называетсябиекцией
(и обозначается
называетсябиекцией
(и обозначается
![]() ),
если она:
),
если она:
Переводит разные элементы множества X в разные элементы множества Y (инъективность). Иными словами,
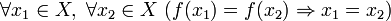 .
.
Любой элемент из Y имеет свой прообраз (сюръективность). Иными словами,
 .
.
Биекцию также называют взаимно однозначным отображением.
(Множества, для которых существует биекция, называются равномощными.)
|
|
Примеры
(
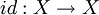 —
функция, сохраняющая все элементы
множестваX,
биективна на этом множестве.)
—
функция, сохраняющая все элементы
множестваX,
биективна на этом множестве.)  —биективные функции
из
—биективные функции
из
 в себя. Вообще, любоймоном
одной переменной
нечетной
степени
является биекцией.
в себя. Вообще, любоймоном
одной переменной
нечетной
степени
является биекцией. f(x) = ex — биективная функция в
 .
Но если её рассматривать как функцию
в
.
Но если её рассматривать как функцию
в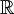 ,
то она уже не будет биективной (у нуля
и отрицательныхчисел
не будет прообразов).
,
то она уже не будет биективной (у нуля
и отрицательныхчисел
не будет прообразов). f(x) = sinx не является биективной функцией, если считать её определённой на всём
 .
.
Функция
 является
биективной тогда и только тогда, когда
существуетобратная
функция
является
биективной тогда и только тогда, когда
существуетобратная
функция
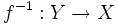 такая,
что
такая,
что и
и .
.Если функции f и g биективны, то и композиция функций
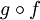 биективна,
в этом случае
биективна,
в этом случае .
Коротко:композиция
биекций является биекцией.
Обратное, вообще говоря, неверно: если
.
Коротко:композиция
биекций является биекцией.
Обратное, вообще говоря, неверно: если
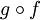 биективна,
то мы можем утверждать лишь, чтоf
инъективна, а g
сюръективна.
биективна,
то мы можем утверждать лишь, чтоf
инъективна, а g
сюръективна.
Можно определить новую функцию:
f-1:B→A, x=f-1(y) – обратная функция, относительно f.
Примеры.
1) f(x)=ex (график)
f:(-∞;+∞)→(0;+∞) f-1: (0;+∞)→(-∞;+∞)
ex=y  x=ln y. f-1=ln
x
x=ln y. f-1=ln
x
2) y=x2 (график)
f:(-∞;+∞)→[0;+∞)
Функция не является (не является инъекцией) взаимно однозначной.
Рассмотрим только одну ветвь f: [0;+∞)→[0;+∞)
x2=y
 x=
x= f-1(x)=
f-1(x)=
Любая строго монотонная функция имеет обратную (т.к. является взаимно однозначной).
