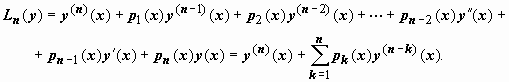63. Уравнение Бернулли. Метод Бернулли

Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в виде

где a(x) и b(x) − непрерывные функции.  Если m = 0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когдаm = 1, уравнение преобразуется в уравнение с разделяющимися переменными.  В общем случае, когда m ≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки

Новое дифференциальное уравнение для функции z(x) имеет вид

и может быть решено способами, описанными на странице Линейные дифференциальные уравнения первого порядка. 

МЕТОД БЕРНУЛИ.

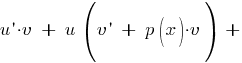
Рассматриваемое уравнение можно решить методом Бернулли. Для этого ищем решение исходного уравнения в виде произведения двух функций:    где u, v - функции от x. Дифференцируем:    Подставляем в исходное уравнение (1):     (2) В качестве v возьмем любое, отличное от нуля, решение уравнения:   (3) Уравнение (3) - это уравнение с разделяющимися переменными. После того, как мы нашли его частное решение v = v(x), подставляем его в (2). Поскольку оно удовлетворяет уравнению (3), то выражение в круглых скобках обращается в нуль. 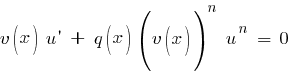Получаем:  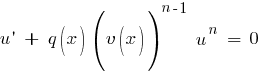    Это также уравнение с разделяющимися переменными. Находим его общее решение, а вместе с ним и решение исходного уравнения y = uv.

64. Уравнение в полных дифференциалах. Интегрирующий множитель. Методы решения

Дифференциальное уравнение первого порядка вида

(1)

называется уравнением в полных дифференциалах, если его левая часть представляет полный дифференциал некоторой функции , т.е.

Теорема. Для того, чтобы уравнение (1) являлось уравнением в полных дифференциалах, необходимо и достаточно, чтобы в некоторой односвязной области изменения переменныхивыполнялось условие

(2)

Общий интеграл уравнения (1) имеет вид или

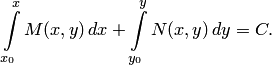
Пример 1. Решить дифференциальное уравнение .

Решение. Проверим, что данное уравнение является уравнением в полных дифференциалах:

так что т.е. условие (2) выполнено. Таким образом, данное уравнение есть уравнение в полных дифференциалах и

поэтому , гдепока неопределенная функция.

Интегрируя, получаем . Частная производнаянайденной функциидолжна равняться, что даетоткудатак чтоТаким образом,.

Общий интеграл исходного дифференциального уравнения .

При интегрировании некоторых дифференциальных уравнений можно так сгруппировать члены, что получаются легко интегрируемые комбинации.

65. Обыкновенные дифференциальные линейные уравнения высших порядков: однородные и неодно-родные. Линейный дифференциальный оператор, его свойства (с доказательством).

Линейный дифференциальный оператор и его свойства. Множество функций, имеющих на интервале (a, b) не менее n производных, образует линейное пространство. Рассмотрим оператор L_n(y), который отображает функцию y(x), имеющую производных, в функцию, имеющуюk - n производных:

(23)

С помощью оператора L_n(y) неоднородное уравнение (20) можно записать так:

Ln(y) = f(x);

(24)

однородное уравнение (21) примет вид

Ln(y) = 0);

(25)

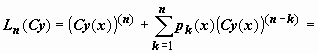
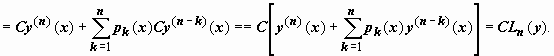
• Теорема 14.5.2. Дифференциальный оператор L_n(y) является линейным оператором.  Док-во непосредственно следует из свойств производных:  1. ЕслиC = const, то 2.

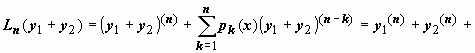
• Линейным дифференциальным уравнением n -го порядка называется уравнение вида  y⁽ⁿ⁾ + a₁(x) y^(n-1) + ... + a_n-1 (x) y' + a_n(x) y = f(x),  где y = y(x) — неизвестная функция,  a₁(x), a₂(x), ..., a_n-1(x), a_n(x),  f(x) — известные функции, которые будем полагать непрерывными на промежутке (a, b).

• Выражение в левой части уравнения называется линейным дифференциальным оператором n -го порядка:  L(y) = y⁽ⁿ⁾ + a₁(x) y^(n-1) + ... + a_n-1 (x) y' + a_n(x) y .  Уравнения  y⁽ⁿ⁾ + a₁(x) y^(n-1) + ... + a_n-1 (x) y' + a_n(x) y = 0 и  y⁽ⁿ⁾ + a₁(x) y^(n-1) + ... + a_n-1 (x) y' + a_n(x) y = f(x),  f(x) № 0,  называются соответственно однородным и неоднородным линейным дифференциальным уравнением n -го порядка.

• Будем записывать однородное и неоднородное линейные дифференциальные уравнения в виде:  L(y) = 0 и L(y) = f(x).

• Принцип суперпозиции основан на следующих свойствах решений линейных уравнений:  а) Если  y₁(x) и y₂(x) — два решения однородного линейного уравнения L(y)=0, то их линейная комбинация y(x) = c₁ y₁(x) + c₂ y₂(x) при любых постоянных c₁, c₂   является решением однородного уравнения.  б) Если y₁(x) и  y₂(x) — два решения неоднородного линейного уравнения  L(y) = f(x), то их разность y(x) = y₁(x) - y₂(x) является решением однородного уравнения L(y) = 0.  в) Любое решение неоднородного линейного уравнения L(y) = f(x) есть сумма частного (фиксированного) решения неоднородного уравнения и некоторого решения однородного уравнения.