1.4. Следствия из теоремы «единственности» первообразной

Следствие 1.1. Если первообразные одной и той же функциисовпадают в одной точке промежутка, то они совпадают во всех точках этого промежутка.

В силу теоремы 1.1. всюду на промежутке ПустьиТогдаСледовательно,ипри всех

Следствие 1.2. Приращение первообразной данной функции на данном промежутке одно и тоже для всех первообразных.

Пусть - первообразные функциина отрезке. Посколькугде, то

Следствие 1.3. Если функция имеет первообразнуюна промежутке, то для любой точкии любого числана промежутке, существует такая первообразнаяфункциичто

Положим Тогда– искомая первообразная.

1.5. Неопределённый интеграл

Определение 1.2. Множество всех первообразных данной функции называютнеопределённым интегралом функции и обозначают символом

–знак интеграла

–подынтегральная функция

–подынтегральное выражение

Пусть – какая-нибудь первообразная функции. Используя теорему 1.1, можно записать

(1.2)

где - любая постоянная.

Операция интегрирования – операция нахождения

первообразной.

Примеры 1.2.

1. .

2. 3..

4. . 5.

Замечание 1.1. Под знаком интеграла принято записывать дифференциал искомой первообразной, а не её производную:а неТакой способ записи целесообразен. Символуказывает переменную, по которой производится интегрирование (переменную интегрирования).

Примеры 1.3.

Найти неопределённый интеграл от функции – это значит найти все первообразные от неё (для чего достаточно указать одну из них). Потому и говорят «неопределённое» интегрирование, что при этом не указывают, какая именно первообразная имеется в виду.

1.6. Проблема существования первообразной

Далеко не всякая функция способна быть производной (т.е. иметь первообразную). Так, у функции , изображённой на рис. 1.1,первообразной нет. Тот факт, что функция имеет разрыв в точкене случаен.

-1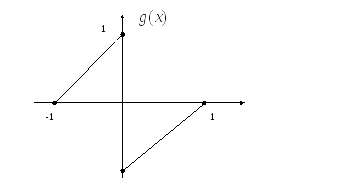

Рис.1.1.

Теорема 1.2. (Существование первообразной). Любая функция, непрерывная на промежутке, имеет на этом промежутке первообразную.

Эта теорема – одна из главных в интегральном исчислении. Она будет доказана в главе 2.

Геометрическая интерпретация доказательства приводится в следующем пункте.

1.7. Геометрическая интерпретация первообразной

Пусть функция непрерывна и неотрицательна на отрезке.

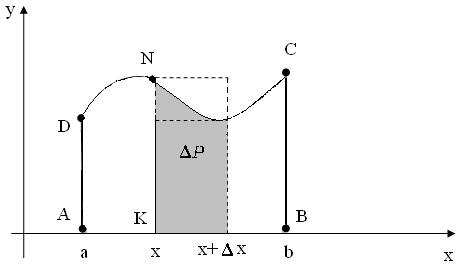
Рис. 1.2.

Рассмотрим криволинейную трапецию , изображённую на рис. 1.2. Определим на отрезкефункциюследующим образом: каждому значениюпоставим в соответствие величинуплощади криволинейной трапеции, заключённой между начальной ординатойи ординатой, отвечающей значению.

Найдём производную функции . Придадим переменнойнекоторое приращение:,. В силу непрерывности функциядостигает на отрезкесвоих наименьшегои наибольшегозначений. Очевидно, площадьзаключена между площадями прямоугольников, построенных на основаниии имеющих высотыи, т.е.

, откуда .

Если значенияибудут изменяться и в силу непрерывности функцииПоэтому

.

Итак,

первообразная непрерывной функции

есть переменная площадь

Среди первообразных функции на отрезке первообразная выделяется тем, что она обращается в в точке. Поэтому

В частности, площадь криволинейной трапециивычисляется по формуле

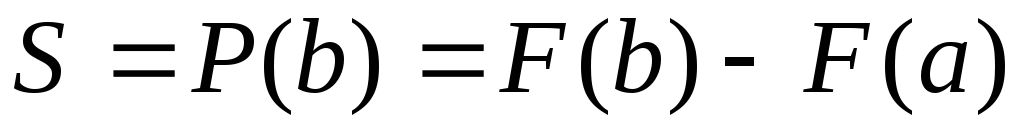
(1.3)

Пример 1.4. Вычислить площадь криволинейного треугольника, заштрихованного на рис. 1.3.

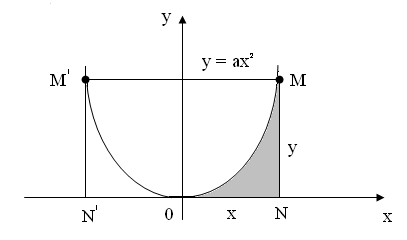
Рис.1.3.

Решение. Первообразная функции есть функция

Используя формулу (1.3), получим

Отсюда следует, что площадь параболического сегмента равнат.е. двум третям площади описанного прямоугольника.

Замечание 1.2. В связи с тем, что между вычислением интегралов и вычислением площадей плоских фигур – квадратурой – существует связь, вычисление интегралов тоже принято называть квадратурой.