
-
Фильтры пространственного дифференцирования и пространственного сглаживания. Текстурные фильтры.
Классификация алгоритмов предварительной обработки
Алгоритмы предварительной обработки изображений подразделятся на различные группы в зависимости от классифицирующего признака. Все алгоритмы предварительной обработки либо должны улучшать в каком – то смысле качество изображений, либо преобразовывать его к виду, наиболее удобному для последующей обработки.
Алгоритмы направленные на улучшение цветовой передачи изображения называются алгоритмами цветокоррекции. В эту группу входят также алгоритмы работающие с полутоновыми изображениями изменяющими их яркостные и контрастные характеристики.
Алгоритмы направленные на обработку пространственных характеристик изображений называются алгоритмами пространственной фильтрации. К этой группе относятся алгоритмы подавления помех, алгоритмы пространственного сглаживания и алгоритмы пространственного усиления, алгоритмы подавления и усиления пространственных частот.
Алгоритмы выполняющие геометрические операции с изображение называются алгоритмами геометрической обработки. К ним относятся:
-
Кадрирование изображение – выделение из исходного изображения некоторой части прямоугольной формы;
-
Изменение размеров изображения. Эти алгоритмы применяют различные методы интерполяции, позволяющие либо корректно восполнить недостающие пикселы в увеличенном изображении, либо пересчитать значения пикселов при уменьшении изображения
-
Поворот изображения. Эти алгоритмы осуществляют поворот исходного изображения на заданный угол, корректно пересчитывая значения пикселов используя различные методы интерполяции.
Алгоритмы выполняющие преобразования из одной цветовой системы в другую называются алгоритмами цветопреобразования. К ним относятся также алгоритмы преобразования цветных изображений в полутоновые и алгоритмы бинаризации, переводящие исходное изображение в бинарное.
Алгоритмы выделяющие на исходном изображении некоторые области по различным, часто неформальным условиям называются алгоритмами сегментации. Примером такого алгоритма может например служить алгоритм, который должен выделять на изображении документа области текста и графической информации или алгоритм выделяющий в в изображении текста области, относящиеся к отдельным словам.
Алгоритмы пространственной фильтрации
Пространственная
фильтрация изображения в математическом
виде представляет собой дискретную
свертку дискретного изображения с
некоторой импульсной характеристикой
пространственного фильтра
где:
Im,
 – матрицы
исходного
и отфильтрованного изображений,
– матрицы
исходного
и отфильтрованного изображений,
 -
матрица импульсной характеристики
фильтра,
-
матрица импульсной характеристики
фильтра,
 – нижняя
и верхняя границы столбцов импульсной
характеристики,
– нижняя
и верхняя границы столбцов импульсной
характеристики,
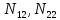 – левая
и правая границы рядов импульсной
характеристики.
– левая
и правая границы рядов импульсной
характеристики.
Матрица импульсной характеристики может быть получена при расчете пространственного фильтра исходя из заданных параметров. Методам расчета пространственных фильтров посвящено большое количество литературы посвященной цифровой фильтрации, например [1]. Для практических расчетов можно использовать стандартные математические пакеты, например в состав системы “MATLAB” входит система расчета фильтров “Image Filter Design”.
Отметим, что фильтрацию можно проводить и в частотной области. В этом случае порядок фильтрации следующий:
-
Перевести изображение из пространственной области в частотную, используя двумерное дискретное преобразование Фурье
-
Осуществить поэлементное умножение частотной матрицы изображения на частотную матрицу фильтра
-
Полученный результат преобразовать в пространственную область, используя обратное двумерное дискретное преобразование Фурье.

Фильтрация изображений в частотной области, применяется достаточно редко из – за большого объема вычислений. Однако такой способ фильтрации широко используется при теоретических выкладках при анализе вариантов обработки изображений. Он позволяет достаточно наглядно представить какого рода фильтрация необходима. Например если нужно выделить на изображении резкие перепады яркости, то очевидно, что необходимо использовать фильтры верхних частот. Наоборот, если нужно избавиться от низкочастотных помех – дрожащих контуров, отдельных выбросов и т.п., то нужно применять фильтры нижних частот. Конкретные параметры фильтров выбираются исходя из частотного анализа помех и свойств исходного изображения.
Фильтры пространственного дифференцирования
Пространственное дифференцирование изображений предназначено для выделения областей, содержащих резкие переходы по яркости или цветности и подавления областей с примерно однородной интенсивностью и цветностью. Иными словами пространственное дифференцирование можно рассматривать как обработку изображения при помощи фильтра высоких частот. Фильтры высоких частот можно можно проектировать по разному, например с помощью классических методов. Однако если их использовать для решения задачи нахождения контуров на изображениях, то обычно сходят из достаточно простых соображений, основывающихся на методах вычисления градиента.
Рассмотрим
полутоновое изображение
 для
получения контурных точек изображения
для
получения контурных точек изображения
 необходимо рассчитать оценки модуля
градиента функции и выявить те точки
изображения, для которых он превышает
некоторый порог.
необходимо рассчитать оценки модуля
градиента функции и выявить те точки
изображения, для которых он превышает
некоторый порог.
Оценки
градиента
 в точке могут быть найдены из оценок
производных функции яркости по двум
ортогональным направлениям. При этом
необходимо выбрать, как эти направления,
так и способ вычисления одномерной
производной. Хорошие результаты дают
окна
в точке могут быть найдены из оценок
производных функции яркости по двум
ортогональным направлениям. При этом
необходимо выбрать, как эти направления,
так и способ вычисления одномерной
производной. Хорошие результаты дают
окна
 с центральным расположением, оцениваемой
точки изображения. Наиболее известными
и быстрыми операторами, работающими с
такими окнами, являются оператор Собела
и оператор Прюитта [1].
с центральным расположением, оцениваемой
точки изображения. Наиболее известными
и быстрыми операторами, работающими с
такими окнами, являются оператор Собела
и оператор Прюитта [1].
В операторе Собела оценки производных в искомой точке формируются на основе взвешенных средних значений интенсивности в точках соседних с ней по вертикали и горизонтали
Рассмотрим
окно
 и обозначим яркости элементов окна
через "a"
– 'i‘:
и обозначим яркости элементов окна
через "a"
– 'i‘:
|
a |
b |
c |
|
d |
e |
f |
|
g |
h |
i |
Оценка
производной
 и
и
 по направлениям
по направлениям
 и
и
 вычисляется следующим образом:
вычисляется следующим образом:

Оценка
градиента
 в точке
в точке
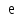 определяется через производные
определяется через производные
 и
и
 как
как
 или через сумму их модулей
или через сумму их модулей
 .
.
В
операторе Прюитта оценки градиента
производятся аналогично. Однако оценки
производной
 и
и
 по направлениям
по направлениям
 и
и
 вычисляются как:
вычисляются как:

Вычисление
оценок градиента по всему полю изображения
с помощью рассмотренных операторов
можно представить как осуществление
процедуры цифровой фильтрации изображения
соответствующими двумерными фильтрами.
Импульсные характеристики этих фильтров
задаются матрицами. Импульсные
характеристики этих фильтров задаются
матрицами. В следующих формулах операция
 представляет
собой поворот матрицы
представляет
собой поворот матрицы
 на 900,
а операция
на 900,
а операция
 -
транспонирование матрицы . Тогда фильтр
Собела для производных
-
транспонирование матрицы . Тогда фильтр
Собела для производных
 и
и
 будет:
будет:
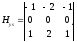
Фильтр
Прюитта для производных
 и
и
 имеет
вид:
имеет
вид:

Операция
цифровой фильтрации изображения
 при
помощи фильтра с конечной импульсной
характеристикой в результате которой
формируется выходное изображение
при
помощи фильтра с конечной импульсной
характеристикой в результате которой
формируется выходное изображение
 ,
представляет собой цифровую свертку
дискретных функций
,
представляет собой цифровую свертку
дискретных функций
 и
и
 .
.
К
часто применяемым дифференцирующим
фильтрам относится фильтр Лапласа. Как
и предыдущие он служит для выделения
границ областей на изображениях. Его
импульсная характеристика, определена
на окне
 и с его помощью сразу получают оценку
градиента, а не производных по вертикальному
и горизонтальному направлению. Импульсная
характеристика фильтра Лапласа имеет
вид:
и с его помощью сразу получают оценку
градиента, а не производных по вертикальному
и горизонтальному направлению. Импульсная
характеристика фильтра Лапласа имеет
вид:
где
 – параметр, выбираемый в пределах от
– параметр, выбираемый в пределах от
 до
до
 .
.
Осуществление операций дифференцирования изображений с помощью фильтрации является универсальным методом, позволяющим единообразно реализовывать различные алгоритмы и операторы дифференцирования. Для этого достаточно реализовать алгоритм вычисления свертки, а сами изображения и различные операторы передавать в этот алгоритм в качестве параметров..
После нахождения оценок градиентов необходимо определить принадлежит ли оцениваемая точка какому либо контуру, имеющемуся на изображении. Это осуществляется при помощи сравнения оценки градиента с некоторым порогом. В случае превышения этого порога считается, что точка принадлежит контуру.
Оценка
порога рассчитывается по уже обработанному
изображению. Обычно, исходя из соображений
минимизации среднеквадратической
ошибки, вносимой случайным шумом, порог
 выбирается
пропорциональным среднему значению
градиента.
выбирается
пропорциональным среднему значению
градиента.
где,
 – ширина
изображения,
– ширина
изображения,
 – высота
изображения,
– высота
изображения,
 – константа,
выбирающаяся эмпирическим путем в
зависимости от желаемой степени
чувствительности обнаружения контурных
точек
– константа,
выбирающаяся эмпирическим путем в
зависимости от желаемой степени
чувствительности обнаружения контурных
точек
 .
.
Пространственное сглаживание
Пространственное сглаживание применяется для уменьшения влияния шума на изображение. Основная идея пространственного сглаживания – замена значения пикселя некоторым «средним» значением, вычисляемым по соседним пикселям находящимся в окрестности обрабатываемого. Следует отметить, что при любом усреднении происходит размытие деталей и ухудшение четкости.
Операцию пространственного сглаживания можно рассматривать как осуществление цифровой фильтрации с помощью фильтра низких частот.
Простейший
сглаживающий фильтр называется
усредняющим.
Каждый элемент импульсной характеристики
этого фильтра равен
 ,
где
,
где
 и
и
 – размеры
окна фильтра. Наиболее распространены
фильтры с окном
– размеры
окна фильтра. Наиболее распространены
фильтры с окном
 .
Для этого фильтра импульсная характеристика
будет:
.
Для этого фильтра импульсная характеристика
будет: 
Фильтр
Гаусса также является фильтром нижних
частот, но по сравнению с усредняющим
фильтром он меньше размывает изображение.
Центральный элемент маски этого фильтра
имеет максимальное значение, соответствующее
пику распределения Гаусса (нормального
распределения). Импульсная характеристика
определена на прямоугольном окне
размером
 ,
а элементы этой характеристики описываются
выражением:
,
а элементы этой характеристики описываются
выражением:
где

Выражение
 определяет двумерное нормальное
распределение, со среднеквадратическим
отклонением
определяет двумерное нормальное
распределение, со среднеквадратическим
отклонением
 .
.
Использование классических фильтров нижних частот довольно ограничено на практике. Эти фильтры плохо работают с помехами типа гауссовский шум, а также с помехами в виде отдельных маленьких областей повышенной и пониженной яркости или цветности (помехи «соль и перец»). При фильтрации таких помех применяют адаптивные и нелинейные фильтры.
Среди
адаптивных фильтров часто используют
фильтр
Винера.
При использовании этого фильтра вычисляют
оценки среднего значения яркости и ее
среднеквадратического отклонения в
пределах окна фильтра и задаются
определенным предполагаемым значением
мощности гауссовского белого шума в
этом же окне. Затем на основе этих оценок
строится импульсная характеристика
данного фильтра. Эта импульсная
характеристика строится так, чтобы
минимизировать дисперсию шумовой
составляющей на выходе этого фильтра
[2].
где
 – область
ближайших соседей пикселя(окна фильтра)
размером
– область
ближайших соседей пикселя(окна фильтра)
размером
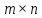 ,
,
 – оценка
среднего значения яркости,
– оценка
среднего значения яркости,
 – оценка
среднеквадратического отклонения
яркости. Тогда элементы импульсной
характеристики фильтра вычисляются
как:
– оценка
среднеквадратического отклонения
яркости. Тогда элементы импульсной
характеристики фильтра вычисляются
как:
где
 – оценка
среднеквадратического отклонения для
шума. В случае если она неизвестна, то
ее находят усреднением по вычисленным
оценкам среднеквадратических отклонений
в окнах фильтрации по всему изображению.
– оценка
среднеквадратического отклонения для
шума. В случае если она неизвестна, то
ее находят усреднением по вычисленным
оценкам среднеквадратических отклонений
в окнах фильтрации по всему изображению.
Фильтр Винера достаточно хорошо подавляет аддитивные случайные гауссовские шумы. Однако его использование для подавления шума с равномерным спектром может приводить к дефокусировке изображения и иногда изображение после такой фильтрации может выглядеть хуже исходного зашумленного изображения.
Ранговая фильтрация является наиболее распространенным методом для построения нелинейных фильтров. Основная идея ранговой фильтрации состоит в замене обрабатываемого пикселя исходного изображения другим пикселем из его ближайшего окружения, выбранным по некоторому алгоритму. Как правило окрестность обрабатываемого пикселя задается прямоугольным окном, называемым маской, а сам исходный пиксель находится в центре этого окна. Элементы маски могут принимать значения равные нулю или единице. Порядком фильтра называется целое число не превышающее общее количество ненулевых элементов маски. Процедура фильтрации происходит следующим образом. Пиксели исходного изображения, соответствующие ненулевым элементам маски, сортируются в порядке возрастания. Пикселю исходного изображения, соответствующему центральному элементу маски, присваивается значение пикселя из отсортированного массива, порядковый номер которого равен порядку фильтра. При обработке всего изображения эта процедура выполняется нерекурсивно, иными словами такой алгоритм применяется к каждому пикселю исходного изображения и соседи определяются именно на исходном изображении. Если изображение не удовлетворяет условиям применения маски (на краях исходного изображения), то оно может быть дополнено нулями либо значениями симметричных пикселей.
Например,
выберем маску размером
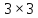 ,
со всеми единичными элементами. Тогда
порядок может иметь значение от
,
со всеми единичными элементами. Тогда
порядок может иметь значение от
 до
до
 .
В зависимости от выбранного порядка,
результат ранговой фильтрации может
быть совершенно разным.
.
В зависимости от выбранного порядка,
результат ранговой фильтрации может
быть совершенно разным.


Маска Изображение Упорядоченные пиксели
При выборе порядка равным 1, произойдет замещение значения 27 центрального пикселя на 22, а при порядке равным 9 – назначение равное 30.
Самым интересным свойством этого алгоритма является создание эффектов расфокусировки (эрозии) и фокусировки (уточнения, наращивания фона и т.д.) изображения. В первом случае порядок фильтра должен быть минимальным, а во втором – максимальным. Меняя порядок фильтра, свойства ранговой фильтрации можно менять в широких пределах.
Эффективным средством фильтрации высокочастотных помех типа «соль и перец» является медианный фильтр, являющийся частным случаем рангового фильтра. Этот фильтр заменяет значение, центрального пикселя на среднее значение, вычисленное по всем соседям, попадающим в маску.
Текстурная фильтрация
Эти фильтры основаны на стандартных статистических характеристиках, измеряемых на изображении
Локальный
ранговый фильтр заменяет
исходные пиксели изображения на их
ранги, вычисляемые по ближайшему
окружению. Обычно используют маску
 .
.![]()





Фильтр среднеквадратических отклонений
Обычно
используют маску
 .
Заменяет центральный пиксель маски на
среднеквадратическое отклонение,
вычисленное по 8 соседям
.
Заменяет центральный пиксель маски на
среднеквадратическое отклонение,
вычисленное по 8 соседям
Энтропийнный фильтр
Обычно
использует используют маску
 .
Заменяет центральный пиксель маски на
энтропию, вычисленное по 80 соседям
.
Заменяет центральный пиксель маски на
энтропию, вычисленное по 80 соседям
где
 – ненулевые значения гистограммы
яркости, построенные по 80 соседям. Всего
столбцов – 256 по числу уровней яркости.
– ненулевые значения гистограммы
яркости, построенные по 80 соседям. Всего
столбцов – 256 по числу уровней яркости.
В
качестве маски в текстурной фильтрации
можно выбирать некоторые интересующие
формы текстуры. Например, такие:


