
formal_language_theory / lectures / unit_3
.pdf
Эквивалентность недетерминированных и детерминированных конечных автоматов
Пример 3.3. Пусть
M = ({q0, q1}, {0, 1}, δ, q0, {q1}) — ndfa, где |
|
|||
δ(q0 , 0) = {q0 , q1}, |
|
δ(q0 , 1) = {q1}, |
|
|
δ(q1 , 0) = , |
|
|
δ(q1 , 1) = {q0 , q1}. |
|
См. рис. 3.4 (а). |
|
|
|
|
|
Start |
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
q0 |
|
q1 |
1 |
|
|
0,1 |
|
|
Рис. 3.4 (a). Недетерминированный автомат M.
51

Пример 3.3.
Построим детерминированный конечный автомат, эквивалентный данному.
Положим |
|
|
|
|
|
|
|
M |
|
(Q ,{0, |
1}, q |
, F ). |
|||
|
|
0 |
|||||
|
|
|
|
|
|
|
|
Согласно теореме 3.3 в качестве |
|||||||
состояний детерминированного |
автомата |
||||||
следует взять все подмножества множества {q0, q1}, включая пустое:
52

Пример 3.3.
Q′ = { , [q0], [q1], [q0 , q1]},
причём |
q |
[q ]. |
0 |
0 |
|
|
|
Конечные состояния автомата
M
пред-
ставлены теми подмножествами, которые содержат конечные состояния данного автомата (в нашем случае q1), т. е.
F
= {[q1], [q0, q1]}.
53

Пример 3.3.
Наконец,
δ′([q0], 0) = [q0, q1], |
δ′([q0], 1) = [q1], |
δ′([q1], 0) = , |
δ′([q1], 1) = [q0, q1], |
δ′([q0, q1], 0) = [q0, q1], δ′([q0, q1], 1) = [q0, q1], |
|
δ′ ( , 0) = , |
δ′( , 1) = . |
Поясним, что δ′([q0, q1], 0) = [q0, q1], так как
δ(q0, 0) = {q0, q1}, δ(q1, 0) = , и {q0, q1} = {q0, q1}.
Аналогично, δ′([q0, q1], 1) = [q0, q1], ибо
δ(q0, 1) = {q1}, δ(q1, 1) = {q0, q1} и
{q1} {q0, q1} = {q0, q1}. См. рис. 3.4 (б).
54
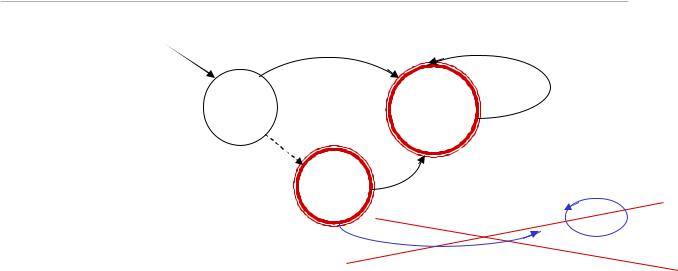
Пример 3.3.
Start
[q0] |
0 |
|
0,1 |
|
||
|
[q0,q1] |
|
||||
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
[q1] |
1 |
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
Рис. 3.4 (б). Детерминированный автомат
M .
Состояние можно удалить как бесполезное (состояние ошибки), ибо из него не достижимо никакое конечное.
55
§3.4. Конечные автоматы
иязыки типа 3
Теперь мы возвращаемся к связи языков, порождаемых грамматиками типа 3, с множествами, которые распознаются конечными автоматами.
Для удобства рассуждений введём понятие
конфигурации конечного автомата, которое относится как dfa, так и к ndfa.
56

Конечные автоматы и языки типа 3
Определение 3.8. Пусть M = (Q, Σ, δ, q0, F)
— конечный автомат.
Конфигурацией конечного автомата M
назовём состояние управления q Q в паре с непрочитанной частью входной цепочки от текущего символа до конца входной
цепочки x Σ*: (q, x).
x
a1 |
a2 |
... |
ai |
ai + 1 |
... |
an |
|
q0 |
q1 |
q |
|
Рис. 3.0 а |
|||
|
|
|
|
|
|||
57

Конечные автоматы и языки типа 3
Пусть (q, ax) — конфигурация fa M, где q Q, a Σ, x Σ*, и пусть
p = δ(q, a) в случае, если M — dfa, или p δ(q, a) в случае, когда M — ndfa.
Тогда fa M может перейти из конфигурации (q, ax) в конфигурацию (p, x), и этот факт мы будем записывать как
(q, ax)  __ (p, x).
__ (p, x).
58

Конечные автоматы и языки типа 3
Далее символом |
|
* |
обозначается |
|
|||
|
|
||
рефлексивно-транзитивное |
замыкание |
||
отношения непосредственного следования
конфигураций |
__ |
на |
множестве |
|
|||
конфигураций. |
|
|
|
Запись
(q0, x)  * ( p, ),
* ( p, ),
где p F, равнозначна записи x T(M).
59

Конечные автоматы и языки типа 3
Теорема 3.4. Пусть G = (VN, VT, P, S) —
грамматика типа 3. Тогда существует конечный автомат M = (Q, Σ, δ, q0, F), такой, что T(M) = L(G).
Доказательство. Построим ndfa M, о
котором идёт речь. В качестве состояний возьмём нетерминалы грамматики и ещё одно дополнительное состояние A VN:
Q = VN {A}, причём начальное состояние автомата M есть q0 = S.
Ret 74 |
60 |
|
