
formal_language_theory / lectures / unit_3
.pdf
Замкнутость rs относительно конкатенации
В последнем случае все дальнейшие движения, благодаря правилу 3, повторяют движения автомата M2.
Если fa M2 принимает (возможно пустое) окончание входной цепочки, принадлежащее языку L2, то и автомат M принимает всю входную цепочку. Другими словами,
T(M) = L1L2.
101

Замкнутость rs относительно замыкания
Определение 3.12. Замыкание языка L
есть множество
|
* |
|
|
k |
|
|
L |
L |
. |
||||
|
|
|||||
|
|
|
k 0 |
|
|
Предполагается, что
L0 = { }, Ln = Ln – 1L = LLn – 1 при n > 0. Пример 3.5. Если L = {01, 11}, то
L* = { , 01, 11, 0101, 0111, 1101, 1111, ...}.
102

Замкнутость rs относительно замыкания
Теорема 3.9. Класс множеств, принимаемых конечными автоматами, замкнут относительно замыкания.
Доказательство. Пусть M = (Q, Σ, δ, q0, F)
— dfa и L = T(M).
Построим ndfa M′ , который распознаёт язык L*.
Положим
M′ = (Q {q0′}, Σ, δ′, q0′, F {q0′}),
где q0′ Q — новое состояние;
Ret 112
103

Замкнутость rs относительно замыкания
для всех a :
|
δ (q0 , a) = |
{δ(q0, a), q0}, если δ(q0, a) F, |
|
|
{δ(q0, a)} в противном случае; |
||
|
|
|
|
для всех q Q и a : |
|||
|
|
|
{δ(q, a), q0}, если δ(q, a) F, |
|
δ (q, a) = |
|
|
|
|
{δ(q, a)} в противном случае. |
|
|
|
|
|
|
|
|
|
|
Предназначение нового начального состояния |
||
q |
|
||
|
0 — принимать пустую цепочку. |
||
Если q0 F, мы не можем просто сделать q0 конечным состоянием, поскольку автомат M может снова прийти в состояние q0, прочитав некоторую непустую цепочку, не принадлежащую языку L.
104

Замкнутость rs относительно замыкания
Докажем теперь, что T(M′ ) = L*.
I. Предположим, что x L*. Тогда либо x = ,
либо x = x1x2...xn, где xi L (i = 1, 2,..., n).
Очевидно, что автомат M′ принимает . Ясно также, что из xi L следует, что
δ(q0, xi) F и множества δ′(q0 , xi) и δ′(q0, xi) каждое содержит состояние q0 и некоторое
состояние p F (возможно p = q0).
105

Замкнутость rs относительно замыкания
Итак,
(q ′, x) = (q ′, x x … x ) |
* (q , x … x ) |
* |
|
||||
|
|
|
|
|
|
|
|
0 |
0 1 2 |
n |
M |
0 2 |
n |
M |
|
|
|
|
|
|
|||
|
|
|
|
|
|
||
… |
* |
(q , x ) |
* (p, ), где p F. |
|
M |
0 n |
M |
|
|
Следовательно, x T(M′ ).
…
106

Замкнутость rs относительно замыкания
II. Предположим теперь, что
(q0 , a1a2...an) |
x = a1a2...an T(M′ ): |
|
|||
__ |
|
|
__ |
__ |
|
M |
(q1 , a2...an) M … |
M |
|||
__ |
__ |
(qn , |
), qi Q (i = 1, 2, …, n), |
||
M (qn 1 , an) |
M |
||||
причём qn F {q0 }. |
|
|
|||
Ясно, что qn = q0 только в случае n = 0. |
|||||
В общем случае существует подпоследо- |
|||||
вательность состояний |
|
|
|||
qi , qi ,..., qi |
(m 1) |
|
|||
1 |
2 |
m |
qik |
q0 , k 1, 2,..., m 1, |
|
такая, что значение |
|||||
|
|
|
|
|
|
|
|
|
qi |
qn F. |
|
|
|
|
m |
|
|
107

Замкнутость rs относительно замыкания
x = a1a2 ... aj1 aj1+1 … aj2 aj2+1 … ajm+1 … an T(M′ )
x1 L |
x2 L |
|
xm L |
q0 |
q0 |
q0 |
q0 |
║ ║ ║
q |
, |
q |
,..., |
q |
, |
|
i |
1 |
|
i |
|
i |
|
|
|
2 |
|
m 1 |
|
|
x = x1x2 ... xm Lm L*.
qim = qn F
108

Замкнутость rs относительно замыкания
Это значит, что в такие моменты ndfa M′ заканчивает просмотр очередного фрагмента x, принимаемого dfa M.
Формально, при некоторых j = jk (1 k m) |
||||||||||||||||
имеет место |
|
|
|
δ, но не δ’ ! |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
q |
|
|
|
, a |
|
), q |
|
δ(q |
|
, |
a |
|
) |
при q |
|
F. |
j |
δ (q |
j |
j |
j |
j |
j |
j |
|||||||||
|
k |
|
k 1 |
|
k |
|
k |
|
k 1 |
|
|
k |
|
|
k |
|
|
|
Поэтому x = x1x2 ... xm, где δ(q0, xk) F для |
||||||||||||||
1 k m. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Это означает, что xk L, |
а |
x Lm L*. |
||||||||||||
Что и требовалось доказать.
109

Теорема 3.10. (С.Клини). Класс множеств, принимаемых конечными автоматами, является наименьшим классом, содержащим все конечные множества, замкнутым относительно объединения, произведения и замыкания.
Доказательство. Обозначим класс регулярных множеств буквой M, а наименьший класс множеств, принимаемых конечными автоматами, содержащий все конечные множества и замкнутый относительно
объединения, произведения и замыкания, буквой 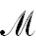 .
.
110
