
Учебник по УМФ первая часть
.pdf
gradω 2 = a12
Следовательно, скорость движения фронта волны будет равна a.
Гл а в а V. Уравнения теплопроводности идиффузии
§1. Уравнение теплопроводности для однородного стержня.
Мы начнем изучение задач теплопроводности и диффузии с простей шего случая –
задачи распространения тепла в тонком однородном стержне с теплоизолированной боковой поверхностью.
Итак, рассмотрим стержень с одинаковой и постоянной плотностью ρ и одинаковой площадью поперечного сечения S по всей длине (которая может быть и бесконечной). Расположим его вдоль оси x (Рис.4.1). Будем считать стержень настолько тонким, что
температуру Т можно считать постоянной по всему поперечному сечению, тогда Т будет
Т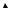
T0 (x)
Т2
Т
x
x |
x + ∆ x |
l |
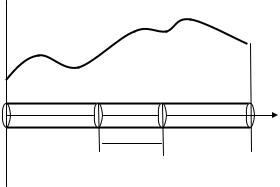
Рис. 25. Распределение температурыпо однородному
стержню в начальный мометвремени
функцией только x и t. Будем также предполагать, что по телу стержня непрерывно распределены источники (или стоки) тепла с объемной плотностью f (x,t) .
Для описания процессов распространения тепла нам необходимо знать такие характеристики материала как удельная теплоемкость с, т.е. количество тепла, которое необходимо сообщить единичной массе вещества, чтобы повысить температуру на один градус, и теплопроводность материала – k, т.е. количество тепла, проходящее в единицу времени через единичную площадку. Эти величины мы будем считатьпостоянными.
Рассмотрим теперь участок стержня длиной x . Количество тепла, необходимое для того, чтобы нагреть его до температуры Т равно
x+∆x
Q = ∫ cT (ξ,t)ρSdξ
x
Тогда изменение этого количества тепла в единицу времени будет определяться выражением
dQ |
|
x+∆x |
∂ |
|
|
|
= cρS |
∫ |
T (ξ,t)dξ |
(1) |
|||
dt |
∂t |
|||||
|
x |
|
|
|||
|
|
|
|
|
||
Положительное изменение количества на участке стержня |
x в нашем случае может |
|||||
происходить за счет того, что количество тепла втекающего в этот участок (через сечение
x) больше потока тепла вытекающего (через сечение x + ∆x ), а также за счет теплопродукции за счет внутреннихисточников тепла.
Поток, как мы помним, пропорционален производной по нормали, в качестве которой в данном случае выступает ось x. Для потока тепла коэффициентом
пропорциональности является теплопроводность, умноженная на площадь поперечного
сечения. Тогда разность потоков тепла через сечения x и x + ∆x выражается следующим образом
|
∂T |
(x + ∆x,t) − |
∂T |
|
, |
(2) |
kS |
∂x |
∂x |
(x,t) |
|||
|
|
|
|
|
а количество тепла, произведенное внутренними источниками тепла в единицу времени, запишется как
|
|
|
|
|
|
x+∆x |
|
|
|
|
|
|
|
|
|
|
∫ |
f (ξ,t)Sdξ |
|
(3) |
|
В результате можем записать |
|
x |
|
|
|
|
||||
|
|
|
|
|
|
|||||
x+∆x ∂ |
|
∂T |
|
|
∂T |
|
x+∆x |
|||
cρS ∫ |
|
|
|
T (ξ,t)dξ = kS |
|
(x |
+ ∆x,t) − |
|
(x,t) |
+ S ∫ f (ξ,t)dξ |
|
∂t |
∂x |
||||||||
x |
|
|
∂x |
|
|
|
x |
|||
Применяя к записанным выше интегралам теоремуо среднем, получим |
||||||||||
cρS |
∂ |
T (x ,t)∆x = kS |
∂T |
(x + ∆x,t) − ∂T |
(x,t) |
+ Sf (x ,t)∆x |
||||
|
|
|||||||||
|
∂t |
ср |
|
|
∂x |
|
ср |
|||
|
|
∂x |
|
|
|
|
||||
Теперь разделим все члены этого равенства c, ρ, S и |
x, после чего устремим |
x кнулю, в |
|||||||||
результате чего точка xср устремится к точке x. В результате получим |
|
||||||||||
|
∂ |
T (x,t) = |
k ∂2T |
(x,t) + |
1 |
f (x,t) |
|
||||
|
|
|
|
|
|
||||||
|
∂t |
сρ ∂x2 |
|
|
|||||||
|
|
|
|
|
|
сρ |
|
||||
Вводя обозначения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
=α2 |
и F(x,t) = |
1 |
f (x,t) |
|
|||
|
|
|
cρ |
|
|
|
cρ |
|
|
|
|
окончательно получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T −α2T |
= F(x,t) |
(4) |
|||||
|
|
|
|
t |
|
xx |
|
|
|
|
|
Это и есть уравнение теплопроводности для однородного стержня, которое является уравнением параболического типа, и в традиционныхобозначенияхбудет иметь вид
u −α2u |
xx |
= F(x,t) |
(5) |
t |
|
|
|
К этому уравнению следует добавить начальное условие |
|
||
u(x,0) =T0 (x) |
(6) |
||
Которое задает распределение температуры в начальный момент времени по всей длине стержня.
§ 2. Граничные условия и их физический смысл.
Рассмотрим ограниченный стержень длиной l (см. Рис.25). Наряду с начальными
условиями (6) в этом случае необходимо, как, сформулировать граничные условия. Также как и для волнового уравнения, для уравнения теплопроводности они могут быть трех
типов.
К граничным условиям первого рода мы приходим в случае, когда на концах стержня задана температура, (не путать с температурой окружающей среды) т.е.
u(0,t) =ϕ(t) |
(7) |
|
u(l,t) =ψ (t) |
||
|
К граничным условиям второго рода нас приводит задание на концах стержня потока тепла, который с точностью до постоянного множителя (при постоянном сечении и
теплопроводности) равен Tx или в обозначениях уравнения (6) ux. В силуэтого граничныхусловияхвторого рода записываются в виде
ux (0,t) =ϕ(t) , ux (l,t) =ψ (t)
имея в виду, что в функцияхφ(t) и ψ(t) учтено деление обеихчастей на множительkS.
в
(8)
Теперь перейдем к заданию меняющейся температуры окружающей среды, граничащей с концами стержня T1(t) и T2(t). В этом случае мы используем закон
теплообмена, по которому поток тепла между телами (или средами) пропорционален разности их температур этих тел (сред). В нашем случае температура на концах самого стержня есть u(0,t) и u(l,t) . Тогда по законутеплообмена
kSux |
(0,t) = h[u(0,t) −T1(t)] |
, |
||
kSu |
x |
(l,t) = −h[u(l,t) −T |
(t)] |
|
|
2 |
|
|
|
где h – коэффициент теплообмена. После деления обеих частей на kS получим окончательный вид граничныхусловий III рода
|
ux |
(0,t) = γ [u(0,t) −T1(t)] |
(–) -? |
(9) |
|
|
ux (l ,t) = −γ [u(l,t) −T2 (t)] |
||||
|
|
|
|||
или в более традиционном виде |
|
|
|||
|
|
|
ux (0,t) −γu(0,t) =ϕ (t) |
|
(10) |
|
|
|
ux (l ,t) +γu(l ,t) =ψ (t) |
|
|
|
|
|
|
|
|
где ϕ (t) = − |
1 T (t), аψ (t) = |
1 T (t). |
|
|
|
|
γ 1 |
γ |
2 |
|
|
§ 3. Применение метода разделения переменных
Мы в очередной раз воспользуемся методом разделения переменных в задаче о распространении тепла в ограниченном стержне длиной l (см.Рис.25) с
теплоизолированной боковой поверхностью без внутренних источников тепла. В этом случае уравнение теплопроводности имеет простой вид:
u =α2u |
xx |
(11) |
t |
|
Первоначальное распределение температуры по стержню задается начальным условием
u(x,0) =ϕ(x) |
(12) |
Как мы помним, для успешной реализации метода разделения переменных граничные условия должны быть однородными. Будем считать, что на границах стержня
поддерживается постоянная нулевая температура
|
u(0,t) = 0 |
|
(13) |
|||
|
u(l |
,t ) = 0 |
|
|||
|
|
|
||||
Представим теперь искомую функцию u(x,t) в в идее произведения |
|
|||||
|
u(x,t) = X (x)T (t) |
(14) |
||||
Подставив это выражение в уравнение (26), получим |
|
|||||
X (x)T ''(t) =α2 X ''(x)T (t) |
|
|||||
Разделим обе части на a2 X (x)T (t) , тогда уравнение приметвид |
|
|||||
|
X ''(x) |
= |
T '(t) |
|
= −λ2 |
(15) |
|
|
2 |
||||
|
X (x) |
a T (t) |
|
|
||
В отличие от применения этого метода для уравнения колебаний ограниченной струны мы обозначили константуразделения через λ2, что не принципиально.
Соотношение (15) позволяет нам записать два уравнения:
X ''(x) +λ2 X (x) = 0 |
(16) |
T '(t) +α2λ2T (t) |
(17) |
Поскольку граничные условия нулевые, это приводит к тому, что и для функции X(x) могут (и должны) быть записаны нулевые граничные условия.
X (0) = 0 и X (l) = 0 |
(18) |
Решение задачи Штурма-Лиувилля для уравнения (16) с граничными условиями (18) нам уже знакомо, мы сразу можем записать найденные собственные числа и
собственные функции. Итак, собственные функции имеют вид
|
|
nπ |
|
|
|
Xn (x) = C2n sin(λn x) , (n = 1,2,3,…) |
||||||||
где λ |
= |
, а |
С |
2n |
– набор произвольных постоянных, |
которые пока не определены. |
||||||||
l |
||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, имеем |
|
|
|
|
nπ x |
|
|
|||||||
|
|
|
|
|
|
X |
n |
(x) = C |
2n |
sin |
, |
(19) |
||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
l |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Обратившись теперь к уравнению (17) с известным уже набором значений λn мы придем кнеобходимости решать бесконечный набор уравнений одного вида
|
|
|
|
|
|
T |
n |
'(t) +α2λ2 T (t) , |
(20) |
||||||
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|||
где λn = |
nπ |
. Решение такого вида уравнений имеет вид |
|
|
|
|
|||||||||
l |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tn (t) |
= Ane |
−α2λ n2 t |
|
|
|
(21) |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
где An – произвольныепостоянные. |
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, для уравнения (14) мы можем записать весь набор решений |
|
||||||||||||||
|
|
u |
n |
(x,t) = X |
n |
(x)T (t) = A |
n |
e−α2λ n2 t |
sin |
nπ x |
|
(22) |
|||
|
|
|
|||||||||||||
|
|
|
|
n |
|
|
|
|
l |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При записи выражения (22) было учтено, что произведение произвольной константы C2n на произвольную константу An будет также давать произвольную константу, которую

можно снова обозначить через An. Как и в случае ограниченной струны (или стержня), каждая из функций Xn(x) представляет собой стоячую волну, а функция Tn – убывающая функция, стремящаяся к нулю при t стремящемся к бесконечности. Таким образом, и
функции un(x,t)при t стремящемся к бесконечности стремятся к тождественномунулю. Сумма всехрешений (22) и будет общим решением уравнения (14)
∞
u (x,t) = ∑u n
n=1
∞ |
|
(x,t) = ∑Xn (x)Tn (t) |
(23) |
n=1
Нам осталось определить константы An. Для этого, как и раньше, мы воспользуемся
начальным условием. Подставляя решение (23) с учетом (22) в начальное условие (12), получим
∑∞ Ansin nπl x =ϕ(x)
n=1
Воспользовавшись, как и в §6 Гл. II, свойством ортогональности системы функций sin(nπx), мы получим выражения для определения коэффициентов An
2 l |
nπξ |
|
|
|
An= l |
∫ϕ (ξ)sin |
l |
dξ |
(24) |
|
0 |
|
|
|
Следует отметить, что общее решение u(x,t) , как и каждая функцияun(x,t), тоже стремится к тождественному нулю при t стремящемся к бесконечности. С физической
точки зрения это означает, что первоначальное распределение температуры вдоль стержня со временем убывает до нуля, если на концах стержня поддерживается нулевая
температура.
В заключении этого параграфа запишем решение нашей задачи полностью
u(x,t) = |
l |
|
∞ |
−( nπα )2 t |
sin nπ x sin nπξ |
|
ϕ (ξ)dξ |
||
∫ |
2 |
∑e |
l |
|
|||||
|
l |
n=1 |
|
l |
|
l |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
При этом мы внесли под знак интеграла функцию |
sin |
nπ x |
, которая не зависит от ξ, а |
||||||
|
|||||||||
|
|
|
|
|
|
|
l |
|
|
также операцию суммирования по n. Изменение порядков суммирования и интегрирования всегда законно при t >0 в силу того, что ряд в скобках сходится равномерно поξ при t >0.
Обозначим выражение в квадратных скобках, которое |
зависит от переменныхx, ξ, t |
||||
через функцию G от этихпеременных |
|
|
|
|
|
G(x,ξ,t) = 2 |
∞ |
nπα 2 |
t sin nπ x sin nπξ |
|
|
∑e−( |
l ) |
(25) |
|||
l |
n=1 |
|
l |
l |
|
|
|
|
|
|
|
Эта функция называется функцией мгновенного точечного источника или более подробно
функцией температурного влияния мгновенного точечного источника тепла. Физический смысл функции G(x, ξ, t) состоит в том, что она представляет собой
температуру в точке x в момент времени t, вызванную действием мгновенного точечного
источника мощностью сρ, помещенного в момент t =0вточкеx = ξ если температура в начальный момент была равна нулю.
Замечание о неоднородных граничных условиях.
В случае ненулевыхграничных условий
|
u(0,t) = µ1(t) |
|
|
(26) |
|||
решение u(x,t) ищут в виде суммы |
u(l,t) = µ 2(t) |
двух слагаемых |
u1 |
и u2, выбрав в |
|||
качестве u1 |
|
|
|
|
|
|
|
u1(x) = µ1 |
(t) + |
x |
[µ2 (t) − µ1(t)] |
|
|
||
|
|
|
|||||
|
|
|
l |
|
|
|
|
Тогда вторую часть u2(x,t) можно искать какрешение уравнения с нулевыми граничными |
|||
условиями: |
|
|
|
u2 |
(0,t) = 0 |
(27) |
|
u2 (l,t) = 0 |
|||
|
|||
При этом сумма двух частей будет |
удовлетворять уравнению с неоднородными |
||
граничными условиями . |
|
|
|
§4. Задача о распространении тепла в изотропном твердом теле.
Рассмотрим твердое тело, температура которого в точке (x,y,z) в момент времени t
определяется функцией u(x, y, z, t).
Как и в случае однородного стержня, нам потребуется знание плотности материала
ρ, удельной теплоемкости с и теплопроводности материала k, которые мы будем считать постоянными.
Для вывода уравнения (функцией температурного влияния мгновенного точечного
источника тепла ия распространения тепла) выделим внутри тела произвольный объем V, ограниченный гладкой поверхностью S, и рассмотрим изменение количества тепла в этом
объеме за промежутоквремени t.
Сначала определим количества тепла, необходимого для изменения температуры элемента объема Δτ за время t = t2 −t1 на величину u = u(x, y,z,t2 )−u(x, y,z,t1):
∆Q1 = c[u(x, y, z,t2 ) −u(x, y, z,t1)]ρ ∆τ
Тогда количество тепла, необходимое для изменение температуры всего тела на ту же величину, будет равно
Q1 = cρ∫∫∫[u(x, y, z,t2 ) −u(x, y, z,t1)]dτ
V
но поскольку
u(x, y, z,t |
2 |
) −u(x, y, z,t ) = t2 ∂u dt , |
|
||
|
|
|
1 |
|
|
|
|
|
|
t∫ ∂t |
|
|
|
|
|
1 |
|
то в результате получим |
|
|
|
|
|
|
|
t |
∫∫∫∂u dτdt |
|
|
Q1 = cρ ∫2 |
(28) |
||||
|
|
t |
V |
∂t |
|
|
|
1 |
|
|
|
Теперь запишем количества тепла, поступающего внутрь объема за промежуток времени t через поверхность S:
t |
∂u ds dt , |
Q2 = −∫2 ∫∫k |
|
t S |
∂n |
1 |
|
где n – внутренняя нормаль к поверхности S. В результате применения формулы ГауссаОстроградского кзаписанномуинтегралуполучим
t2 |
|
t2 |
|
|
Q2 = k ∫∫∫∫div(grad u)dτdt = k ∫∫∫∫∆udτdt |
(28) |
|||
t1 |
V |
t1 |
V |
|
Посчитаем также количества тепла, произведенного за тот же промежуток времени внутренними источниками тепла, непрерывно распределенных по объему V с плотностью
f(x,y,z,t). Оно будет равно
|
|
t2 |
|
|
|
|
|
Q3 = ∫∫∫∫ f (x, y, z,t)dτ dt |
(29) |
||||
|
|
t1 |
V |
|
|
|
Исходя из условия баланса, можно |
записать, |
что Q1 = Q2 +Q3 . |
Согласно этому |
|||
условию мы получим |
|
|
|
|
|
|
t |
∫∫∫∂u dτdt |
t |
|
t |
|
|
cρ ∫2 |
= k ∫2 |
∫∫∫∆udτdt + ∫2 ∫∫∫ f (x, y, z,t)dτ dt |
|
|||
t |
V ∂t |
t |
V |
t |
V |
|
1 |
|
1 |
|
1 |
|
|
Так как подынтегральная функция непрерывна, а объем V |
и промежуток времени t |
||||
произвольны, то можем записать |
|
||||
|
|
cρ ∂u = k∆u + f (x, y, z,t) |
|
||
|
|
∂t |
|
||
или, вводя величины α2 = |
k |
и F(x, y, z,t) = |
f (x, y, z,t) |
, окончательно будем иметь |
|
cρ |
|
||||
|
|
cρ |
|
||
|
|
∂u =α2∆u + F(x, y, z,t) |
(30) |
||
|
|
∂t |
|
||
Это и есть уравнение теплопроводности однородного изотропного тела, которое
представляет собой уравнение Пуассона в пространстве.
В отсутствии источников тепла оно переходит в уравнение Лапласа
∂u =α2∆u |
(31) |
∂t |
|
Для полной постановки задачи нужно сформулировать |
начальное условие и |
граничные условия. |
|
В начальный момент времени задается распределение температуры по |
|
рассматриваемомуобъемув начальный момент времени, а именно |
|
u(x, y, z,0) =ϕ(x, y, z,) |
(32) |
Граничное условие, каки раньше, может быть задано тремя основными способами: 1) в каждой точке ограничивающей поверхности S задается температура
u |S =ψ (P,t) , |
(33) |
где P – текущая точка на поверхности S;
2) на поверхности S задается тепловой поток
q = −k ∂∂un ,
откуда можно записать
∂u |
|S = χ(P,t) |
(34) |
∂n |
|
|
3) на поверхности S происходит теплообмен с окружающей средой, температура которого известна и может быть функцией времени T(t). Тогда по закону Ньютона о теплообмене
q = h (u −T ) ,
где h – коэффициент теплообмена, который мы будем считать постоянным. h (u −T (t)) |S = −k ∂∂un |S
или, положив γ = kh , окончательно получим
∂u |
+γ (u −T (t)) |S = 0 |
(35) |
∂n |
|
|
§ 5. Уравнение диффузии
Если среда неравномерно заполнена газом, то имеет место диффузия его из мест с более высокой концентрацией в места с меньшей концентрацией. Сходное явление имеет
место и в растворах, если концентрация растворенного вещества в среде не постоянна. Рассмотрим процесс диффузии в полой трубке или в непроницаемой трубке,
заполненной пористой средой. При этом мы будем предполагать поперечное сечение трубки S настолько малым, что концентрацию газа или раствора в поперечном сечении можно считать постоянной. Будем также считать, что источники вещества в трубке
отсутствуют. Процесс диффузии может быть описан функцией u(x,t), представляющей концентрацию в сечении x в моментвремениt.
Согласно закону Нерста масса газа, протекающая через сечение x за промежуток времени (t, t + t) равна
dQ = −D |
∂u |
(x,t) dt , |
(36) |
|
∂x |
|
|
где D – коэффициент диффузии.
Исходя из определения концентрации, изменение массы газа на участке трубки (x1,x2)приизменении концентрации на величину u равно
x2 |
|
∆Q = ∫ c(x) ∆u Sdx , |
(37) |
x1 |
|
где c(x) – коэффициент пористости среды, который есть отношение суммарного объема пор кполномуобъему, в нашем случае равномуSdx.
Теперь составим уравнение баланса массы газа на участке (x1,x2) за промежуток времени (t1, t2):

t2 |
|
∂u |
(x2 |
,τ) − D(x1) |
∂u |
|
x2 |
S ∫ |
D(x2 ) |
∂x |
∂x |
(x1,τ) dτ = S ∫ c(ξ)[u(ξ,t2 ) −u(ξ,t1)]dξ |
|||
t |
|
|
|
|
x |
||
1 |
|
|
|
|
|
|
1 |
Откуда, также каки в предыдущем параграфе, получим
∂∂x (D ∂∂ux ) = c ∂∂ut ,
которое и является одномерным уравнением диффузии.
Если коэффициент диффузии постоянен, то с учетом обозначенияα2 = Dc диффузии приобретает вид
(38)
уравнение
u −α2u |
xx |
= 0 , |
(39) |
t |
|
|
который аналогичен одномерному уравнению теплопроводности в отсутствии источников тепла.
§6. Принцип максимального значения
Вэтом параграфе мы докажем свойство решений одномерного уравнения теплопроводности, которое называется принципом максимального значения. Оно может быть сформулировано кактеорема.
Те о р е м а. Если функция u(x,t), определенная и непрерывная в замкнутой области
0 ≤ t ≤T и 0 ≤ x ≤ l , удовлетворяет в этой области уравнению теплопроводности
u =α2u |
xx |
, |
(40) |
t |
|
|
то максимальное и минимальное значения функции u(x,t) достигаются или в начальный момент времени или в граничных точках x = 0 или x = l.
Функция u(x,t) = const , очевидно, удовлетворяет уравнению (40) и достигает своего
максимального (минимального) значения в любой точке. Однако это не противоречит теореме, так как из её условия следует, что если максимальное (минимальное) значение
достигается внутри области, то оно также должно достигаться или при t=0, или при x =0 или при x=l.
Физический смысл этой теоремы очевиден и заключается в следующем. Если температура на границе или в начальный момент не превосходит некоторого значения M, то при отсутствии источников тепла внутри тела не может создаться температура, больше
чем М.
Остановимся на доказательстве теоремы для максимального значения. Оно ведется
от противного. Итак, пусть М – максимальное значение функции u(x,t) при t = 0 (0 ≤ x ≤ l) или при x = 0 или при x = l (0 ≤ t ≤ T). Допустим теперь, что в некоторой точке области (x0, t0), такой, что 0 < x0 < l и 0 < t0 ≤ T , функция u(x,t) достигает своего максимального
значения, превосходящего М на величину ε, т.е.
u(x0 ,t0 ) = M +ε
Тогда в точке (x0, t0) должнывыполняться соотношения
∂u |
(x |
,t |
|
) = 0 и |
∂2u |
(x |
,t |
|
) ≤ 0 |
(41) |
∂x |
|
∂x2 |
|
|||||||
0 |
|
0 |
|
0 |
|
0 |
|
|
Далее так какu(x0, t) достигает максимального значения при t = t0 , то
