
Учебник по УМФ первая часть
.pdf
взятый по поверхности сферы Sat радиуса r = at с центром в точке M (x,y,z), является
решением волнового уравнения (9), причем функция w(ξ,η,ζ) является произвольной. Координаты сферы Sat могут быть выражены по формулам
ξ = x +αat , η = y + βat , ζ = z +γat
где α, β, γ – направляющие косинусы текущего радиуса сферы Sat , которые, как известно, могут быть записаны в виде
α = sinθ cosϑ , β = sinθ sinϑ , α = cosθ ,
где угол θ меняется от 0 до π и угол ϑ от 0 до 2π. Когда точка (ξ,η,ζ) описывает сферу Sat , точка (α, β, γ) описывает сферуS1 единичного радиуса с центром в начале координат,
а между соответствующими элементами площади dσr и dσ1 обеих сфер имеется соотношение
dσr = r2dσ1 = a2t2dσ1 = a2t2 sinθdθdϑ
Тогда интеграл (11) приводится квиду
|
4π ∫∫S |
|
|
|
u(x, y, z,t) = |
t |
|
w(x +αat, y + βat, z +γat)dσ1 |
(12) |
|
||||
1 |
|
|
||
Отсюда легко заметить, что функция u(x, y, z,t) имеет непрерывные производные до
k-го порядка, если функция w (ξ,η,ζ) непрерывна вместе со своими производными до k-го
порядка.
Из формулы (12) находим
∆u = 41π ∫∫S1 ∆wdσ1
или, возвращаясь кпервоначальной области интегрирования
|
4πa2t |
∫∫ |
|
|
∆u = |
1 |
|
∆wdσr |
(13) |
|
|
Sat
Дифференцируя теперь выражение (12) по t, получим
u t = |
1 |
∫∫S |
w(x +αat, y + βat, z +γat)dσ1 + |
|
||||||||||
4π |
|
|||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
(14) |
||
|
|
at |
|
|
|
∂w |
|
∂w |
|
∂w |
||||
|
|
|
|
|
|
|
||||||||
+ |
|
∫∫S |
|
α |
|
+ β |
|
+γ |
|
|
|
|||
4π |
|
∂ξ |
∂η |
∂ζ |
|
|||||||||
|
|
|
|
|
|
|
|
dσ1 |
|
|||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Чтобы вычислить ∂2u , перепишем последнее выражение в виде
∂t2
u t= |
u |
+ |
1 |
∫∫ |
|
α |
∂w |
+ β |
∂w |
+γ |
∂w |
|
t |
|
|
∂ξ |
∂η |
|
|
||||||
4πat |
∂ζ |
|||||||||||
|
|
Sat |
|
|
|
|
dσr |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и, применив формулуОстроградского, получим
u |
|
1 |
∫∫∫D |
|
u t = t |
+ |
|
∆u dξdηdζ |
|
4πat |
||||
|
|
|
at |
|
где Dat – шар радиуса r = at с центром в точке M (x,y,z). Обозначая в этой формуле определенный интеграл через I, мы можем переписать её в виде
|
|
|
|
|
|
u t = u |
|
+ |
I |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
4πat |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
||
Дифференцируя это выражение по t, |
получим |
|
|
|
|
|
|
|
||||||||||||
u tt = − |
u |
|
1 |
u |
|
1 |
|
|
|
|
|
1 |
|
|
1 ∂I |
|
1 ∂I |
(15) |
||
|
+ |
|
|
+ |
|
|
− |
|
|
|
|
+ |
|
|
= |
|
|
|||
t2 |
t |
|
|
|
4πat2 |
4πat ∂t |
4πat ∂t |
|||||||||||||
|
|
t |
|
4πat |
|
|
|
|
|
|||||||||||
Теперь убедимся, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂I |
= a |
∫∫ |
∆wdσr |
|
|
|
|
|
(16) |
|||||
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Sat |
|
|
|
|
|
|
|
|
|
||
Действительно, переходя в интеграле I к сферическим координатам (ρ,θ,ϑ) с центом в точке M (x,y,z), имеем
|
|
|
|
|
at 2π π |
|
|
|
||
|
|
|
|
I = ∫ |
∫ ∫∆wρ2 sinθdθdϑd ρ |
|
|
|||
|
|
|
|
|
0 |
0 |
0 |
|
|
|
Теперь дифференцируя это выражение по t, получим |
|
|
||||||||
∂I |
= a |
2π π |
∂2w |
+ |
∂2w |
+ |
∂2w |
a2t2 sinθdθdϑ = a |
∫∫ |
∆wdσr |
∂t |
|
∂ξ2 |
∂η2 |
|
||||||
|
∫ ∫ |
|
|
∂ς2 |
|
|
||||
|
|
0 0 |
|
|
|
|
ρ=at |
|
Sat |
|
Сравнивая (13), (15) и (16) убеждаемся, что функция u(x, y, z,t) , определяемая формулой
(11), удовлетворяет волновому уравнению (9), какова бы ни была функция w(x,y,z), имеющая производные до второго порядка включительно.
Из формул (12) и (14) следует, что в этом виде функция u удовлетворяет начальным условиям
u(x, y, z,0) = 0 |
|
(17) |
|
u t(x, y, z,0) = w(x, y.z) |
|||
|
|||
Тогда, если функция u есть решение волнового уравнения (9) с начальными |
|||
условиями (17), то можно убедиться, что функция |
∂u |
|
|
v(x, y, z,t) = |
|
||
|
∂t |
|
|
будет также решением уравнения (9), удовлетворяющим начальным условиям |
|
||
v(x, y, z,0) = w(x, y.z) |
(18) |
||
vt(x, y, z,0) = 0 |
|
||
|
|
||
Взяв теперь в качестве функции w(x,y,z) |
в начальных условиях (17) функцию |
||
ψ (x, y.z), а в начальных условиях (18) функциюϕ (x, y.z) и сложив построенные таким
образом решения, мы получим решение уравнения (9), удовлетворяющее начальным условиям (10).
Таким образом, решение уравнения (9), удовлетворяющее начальным условиям (10),
запишется в виде |
|
|
|
||||
u(x, y, z,t) = |
1 |
|
∂ |
∫∫ϕ(ξ,rη,ς) dσr + |
1 |
∫∫ψ (ξ,rη,ς) dσr |
(19) |
4πa |
∂t |
4πa |
|||||
|
|
|
|
Sat |
|
Sat |
|
Эта формула называется формулой Пуассона.
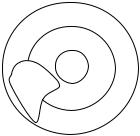
Физическая картина распространения волн в трехмерном пространстве
Чтобы яснее представить физическую картину распространения волн в трехмерном пространстве, описываемое формулой Пуассона (19), положим, что начальное
возмущение сосредоточено в некоторой ограниченной области D с границей S, т.е. функции φ и ψ равны нулю вне области D. Пусть точка M (x, y, z) находится вне области D. Обозначим через d и l соответственно наименьшее и наибольшее расстояния от точки
M до точекповерхности S (Рис. 17). При t < da сфера Sat находится вне области D, а значит функции φ и ψ равны нулю на сфере Sat, тогда из формулы (19) имеем u (M, t) = 0.
|
|
|
|
|
|
Sat3 |
Иначе говоря, начальное возмущение ещё не успело |
||||
|
|
|
|
|
|
|
дойти до точки M. В моментt = d сфера Sat коснется |
||||
|
|
|
|
|
Sat2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sat1 |
|
|
|
|
||||
|
|
|
|
|
поверхности S и передний фронт волны накроет точку M. |
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
Начиная |
с этого момента, сфера |
Sat начинает пересекать |
M |
|||||||||||
|
D |
|
|
|
|
|
|
|
область |
D и согласно формуле |
(19), мы будем иметь |
|
|
|
|
|
|
|
|
|
u(M ,t) ≠ 0 . Наконец, при t > D |
сфера Sat снова не будет |
|
|
|
|
|
|
|
|
|
|
|
a |
|
Рис. 21. Расширение сферы Sat |
иметь общих точек с поверхностью S (вся область D будет |
||||||||||
лежать внутри сферы Sat) и согласно формуле (19) мы |
|||||||||||
будем снова иметь u(M, t) = 0. Моменту времени t = Da соответствует прохождению заднего фронта волны через точкуM.
Из изложенного следует, что передний фронт волны в заданный момент времени представляет собой поверхность, отделяющую точки, которые ещё не начали колебаться от точек, которые уже колеблются. Все точки этого фронта имеют кратчайшее расстояние
от S, равное at. Иначе говоря, передний фронт волны есть огибающая семейства сфер, имеющих центры на поверхности S и радиус, равный at. Задний фронт волы в заданный момент времени t представляет собой поверхность, отделяющую точки, которые ещё
продолжают колебаться от точек, которые уже не колеблются. Постоянная a является скоростью распространения, какпереднего, таки заднего фронта волны.
§ 2. Двумерное волновое уравнение
Обратимся к формуле (19) предыдущего параграфа и рассмотрим частный случай, когда функции φ и ψ зависят только от координат x и y. Если передвигать точку M (x,y,z)
параллельно оси О z, то правая часть формулы Пуассона не будет менять своего значения, а тогда и функция u не будет зависеть от z и формула (19) даст решение уравнения
utt = a2 (u xx +uy y ) |
(20) |
при начальныхусловиях |
|
|
|
u(x, y,0) =ϕ (x, y) |
(21) |
||
ut (x, y,0) |
=ψ (x, y) |
||
|
|||
Таким образом, мы можем пользоваться решением (19) оставаясь на плоскости (x, y). Для этого надо инт егралы в формуле (19), которые берутся по поверхностям сфер, преобразовать в интегралы по площади кругов на плоскости (x, y). Для этого возьмем
точкуМ(x, y) на плоскости (x, y). При этом точки с координатами (ξ,η,ζ), определяемыми по формулам
ξ = x +αat , η = y + βat , ζ = z +γat
при z = 0 будут переменными точками сферы Sat с центром в точке M (x,y,0) и радиусом at. Обе части этой сферы, находящиеся над и под плоскостью (x, y), проектируются на эту плоскость в виде круга Cat с центром в точке M (x,y,) и радиусом at. Известно, что
dCat = cos(n, z) dσat
где n – нормаль к поверхности сферы, совпадающая по направлению с её радиусом. Если N – переменная точка на сфере, а N1 – её проекция на плоскость (x, y), то
cos(n, z) = |
|
a2t2 |
−(ξ − x)2 −(η − y)2 |
, |
|
|
at |
||
|
|
|
|
где (ξ,η,) – координаты переменной точки круга Cat.
Таким образом, в результате преобразования формулы (19) мы получим
|
|
|
1 |
|
∂ |
|
|
ϕ(ξ,η) |
|
|
|
|
||||
u(x, y,t) = |
|
|
|
|
|
|
C∫∫at |
|
|
|
|
|
dξdη + |
|||
|
2πa |
∂t |
|
|
|
|
|
|||||||||
|
|
|
|
a2t2 −(ξ − x)2 −(η − y)2 |
||||||||||||
|
|
|
1 |
|
∫∫ |
|
|
|
ψ (ξ,η) |
(22) |
||||||
|
+ |
|
|
|
|
|
dξdη |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
a2t2 −(ξ − x)2 −(η − y)2 |
||||||||||
|
|
|
|
2πa Cat |
|
|
|
|
|
|||||||
Эта формула дает решение однородного волнового уравнения (20), удовлетворяющее начальным условиям (21).
§ 3. Теорема единственности для двумерного волнового уравнения
Докажем единственность решения волнового уравнения при заданных начальных
условиях. Для простоты записи будем считать a =1, чего можно всегда достигнуть, меняя масштаб времени заменой t на t/a. Для большей наглядности рассмотрим двумерное
волновое уравнение, т.е. для u (x,y,t)
∂2u |
= |
∂2u |
+ |
∂2u |
(23) |
|
∂t2 |
∂x2 |
∂y2 |
||||
|
|
|
||||
c начальными условиями |
|
|
|
|
|
|
u(x, y,0) = f (x, y) |
|
|||||
∂u (x, y,0) = g(x, y) |
(24) |
|||||
|
||||||
∂t |
|
|
|
|
|
|
Докажем единственность решения задачи Коши (23) – (24), предполагая, что решение
u(x,y,t) имеет непрерывные производные до второго порядка включительно.
Пусть u1(x,y,t) и u2(x,y,t) – два решения уравнения (23), удовлетворяющие одним и тем же начальным условиям (24). Тогда разность
u (x, y,t)= u (x, y,t)1 −u (x, y,t)2
будет удовлетворять уравнению (23) и нулевым начальным условиям u(x, y,0) = 0
∂∂ut (x, y,0) = 0
Для доказательства теоремы единственности нам надо теперь показать, что любыхx,y и привсех t >0.
(25)
u ≡ 0 при
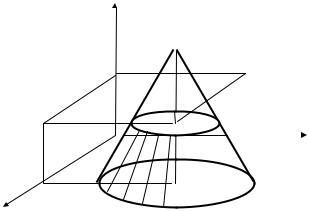
Рассмотрим для этого произвольную точку М(x0,y0,t0), круговой конус
трехмерное пространство (x,y,t) и возьмем в нем причем t0 >0. Из этой точки как из вершины проведем
(x − x0 )2 +(y − y0 )2 −(t −t0 )2 = 0
до его пересечения с плоскостью t = 0(Рис.22). Далее проведем еще одну плоскость t = t1,
где 0 < t1 < t0 , и пусть |
D – |
область, ограниченная боковой поверхностью конуса |
S и |
частями поверхностей |
t = 0 |
и t = t1, находящихся внутри конуса. Иначе говоря, D |
– |
усеченный круговой конус. Обозначим через σ0 и σ1 – соответственно нижнее и верхнее
основания этого конуса.
Теперь в приведенном ниже выражении произведем указанные в нем операции
дифференцированияи приведем подобные члены |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
∂ |
|
∂u 2 |
|
∂u |
2 |
|
∂u 2 |
|
|
|
|
|
|
∂ ∂u ∂u |
|
|
|
∂ |
|
∂u ∂u |
|
|
∂u ∂2u |
|
|
|
∂u ∂2u |
|
∂u ∂2u |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
= 2 |
|
|
|
|
|
+ 2 |
|
|
|
|
|
|
|
|
|
+ 2 |
|
∂t2 |
+ |
|||||||||||
|
∂t |
∂y |
∂t |
|
|
|
|
∂t ∂x |
|
|
|
∂t ∂y |
∂x ∂t∂x |
∂y ∂t∂y |
∂t |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
∂x |
|
|
|
|
|
|
|
|
|
∂x |
|
|
∂y |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
∂2u ∂u |
−2 |
∂u ∂2u |
−2 |
|
∂2u ∂u |
|
−2 |
∂u ∂2u |
= 2 |
|
∂u |
∂2u |
− |
∂2u |
− |
∂2u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
∂t ∂x2 |
|
|
|
|
|
|
|
|
|
|
∂t ∂y2 |
|
|
|
∂t2 |
∂x2 |
∂y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
∂x∂t ∂x |
|
∂y∂t ∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
В результате получим тождество |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
∂u |
∂2u |
|
∂2u |
|
∂2u |
|
|
|
|
∂ |
|
∂u 2 |
|
∂u |
2 |
|
∂u 2 |
|
∂ ∂u ∂u |
|
|
|
|
∂ |
|
∂u ∂u |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
2 ∂t |
|
2 |
|
− ∂ 2 |
− ∂ |
|
2 |
|
= |
|
|
|
|
∂x + |
∂y |
|
+ |
|
∂t |
|
−2 |
|
∂t |
∂x |
−2 |
|
|
|
|
∂t ∂y |
|
|
||||||||||||||||||||||||||
|
|
|
|
∂ |
|
|
∂t |
∂x |
∂y |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
t |
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Проинтегрируем это тождество по объему, |
занимаемому областью D. |
Интеграл от |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
левой части равен нулю, так как u |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
является решением уравнения (23). |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. М(x0,y0,t0) |
|
|
|
|
|
|
|
Интеграл в правой части преобразуем, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пользуясь |
|
формулой |
|
|
Гаусса- |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Остроградского, |
|
в |
|
интеграл по |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поверхности |
|
|
|
|
этой |
|
|
области, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
составленной из поверхностей S, σ0 |
и |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ1. |
В результате получим сумму трех |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поверхностных интегралов от одного |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и того же выражения, при записи |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которого |
|
|
|
нужно |
|
учесть, |
что |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
∂ |
|
∂ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
производные |
|
|
, |
, |
, стоящие |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
∂x |
|
∂y |
|||||||||||||||||
|
|
|
|
|
|
Рис. 22.Усеченный конус D |
|
|
|
|
|
|
|
|
|
|
перед |
|
|
|
|
скобками, |
|
|
|
|
являются |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
производными по направлениям t, x, y |
|||||||||||||||||||||||
инаправляющие косинусы будут соответственно равны cos(nt), cos(nx) cos(ny) .
Врезультате получим
∫∫L (x, y,t) ds + ∫∫L (x, y,t) ds + ∫∫L (x, y,t) ds = 0 ,
|
S |
|
|
σ0 |
σ1 |
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u 2 |
|
∂u 2 |
|
∂u 2 |
|
∂u ∂u |
|
∂u ∂u |
|||
L (x, y,t) = |
|
+ |
|
+ |
|
cos(nt) −2 |
|
∂t |
cos(nx) −2 |
|
∂t |
cos(ny) |
|
∂x |
|
∂y |
|
∂t |
|
|
∂x |
|
∂y |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
(26)
(27)
На нижнем основании σ0 усеченного конуса D, в силу начальных условий (25), функция u и все её частные производные первого порядка равны нулю и, следовательно, второй интеграл в (26) равен нулю. На верхнем основании σ1 имеем
cos(nx) = cos(ny) = 0, cos(nt) =1
На боковой поверхности конуса S направляющие косинусы нормали удовлетворяют соотношению
cos2 (nt) −cos2 (nx) −cos2 (ny) = 0 |
(28) |
В результате равенство (26) с учетом (27) можно переписать следующим образом
|
|
|
|
|
∂u |
2 |
|
∂u |
2 |
∂u |
2 |
|
|
∫∫S |
|
|
|
|
|
|
|||||||
|
|
∂x |
|
|
∂y |
|
|
∂t |
|
||||
|
|
|
|
|
|
+ |
|
|
+ |
|
|
cos(nt) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
∫∫ |
∂u 2 |
∂u 2 |
∂u 2 |
|||||||||
|
∂x |
|
∂y |
|
∂t |
|
|||||||
|
|
|
|
+ |
|
+ |
|
ds |
|||||
|
σ1 |
|
|
|
|
|
|
|
|
|
|
||
−2 |
|
∂u ∂u |
|
∂u ∂u |
||
|
∂t |
cos(nx) −2 |
|
∂t |
cos(ny) |
|
|
|
∂x |
|
∂y |
||
Первый интеграл с учетом (28) можно преобразовать следующим образом
ds +
(29)
|
|
|
1 |
|
|
∂u |
|
2 |
|
∂u |
2 |
∂u |
|
2 |
|
|
2 |
|
|
|
∂u ∂u |
|
|
|
||||||||
∫∫S |
|
|
|
|
|
|
+ |
+ |
|
|
|
(nt) −2 |
|
|
|
|||||||||||||||||
cos(nt) |
∂x |
|
|
|
∂y |
∂t |
|
|
|
|
|
∂t |
∂x |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
cos(nx) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
2 |
cos |
2 |
|
|
∂u ∂u |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(nt)−2 |
|
|
|
cos(nx) cos(nt)+ |
|
|
||||||||||||
= ∫∫ |
|
1 |
|
|
∂x |
|
|
|
|
|
|
|
∂t ∂x |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
cos(nt) |
|
|
∂u |
|
|
|
|
|
|
∂u ∂u |
|
|
|
|
|
|
|
∂u |
||||||||||||||
|
S |
|
|
|
|
cos |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
+ |
|
|
2 (nt)−2 |
cos(ny) cos(nt)+ |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
∂t ∂y |
|
|
|
|
|
∂t |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
∂u |
|
|
|
|
|
|
∂u |
|
|
|
|
2 |
|
|
∂u |
|
|
|
∂u |
|
|
|
||
= ∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
cos(nt) − |
|
cos(nx) |
+ |
|
|
cos(nt) |
− |
|
cos(ny) |
||||||||||||||||
|
cos(nt) |
∂x |
∂t |
∂y |
∂t |
|||||||||||||||||||||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 ∂u ∂u
∂t ∂y
2 cos2(nx)
2 ds
cos(ny) ds =
ds = +cos2(ny)
На боковой поверхности S cos(nt) =  22 и, следовательно, этот интеграл неотрицателен, из чего приходится заключить, что второй интеграл в формуле (29) равен нулю, а именно
22 и, следовательно, этот интеграл неотрицателен, из чего приходится заключить, что второй интеграл в формуле (29) равен нулю, а именно
∫∫ |
∂u 2 |
∂u 2 |
∂u 2 |
||||
|
∂x |
|
∂y |
|
∂t |
|
|
|
|
|
+ |
|
+ |
|
ds = 0 |
σ1 |
|
|
|
|
|
|
|
Отсюда следует, что во всех точках внутри полного конуса с вершиной в точке
М(x0,y0,t0) частные производные первого порядка функции u равны нулю и, следовательно сама u равна константе, а поскольку на нижнем основании эта константа в силу (25) равна
нулю, то и в точке М(x0,y0,t0) она равна нулю. Поскольку точка М(x0,y0,t0) была нами выбрана произвольно в полупространстве t >0, то составленная нами функция u тождественно равна нулю в этом полупространстве, что и доказывает теорему
единственности.
§ 4. Трехмерное неоднородное волновое уравнение
Рассмотрим трехмерное неоднородное волновое уравнение
∂2u |
= a |
2 |
|
∂2u |
+ |
∂2u |
+ |
∂2u |
+ F(x, y, z,t) |
(28) |
|
∂t2 |
|
|
∂x2 |
∂y2 |
∂z2 |
|
|||||
|
|
|
|
|
|
|
|
||||
и будем искать его решение, удовлетворяющее нулевым начальным условиям
u(x, y, z,0) = 0 |
|
||
∂u |
(x, y, z,0) |
= 0 |
(29) |
|
|||
∂t |
|
|
|
Это означает, что в исходном состоянии описываемый объект не был деформирован и покоился. В этом случае деформации этого объекта в последующие моменты времени
будут определяться только внешней силой F(x, y, z,t) и механическими свойствами
объекта.
Чтобы решить поставленную задачунужно решить однородное уравнение
∂2v |
= a |
2 |
|
∂2v |
− |
∂2v |
− |
∂2v |
(30) |
|
∂t2 |
|
|
∂x2 |
∂y2 |
∂z2 |
|
||||
|
|
|
|
|
|
|
||||
но с ненулевой начальной скоростью, равной внешней силе из уравнения (28) в некоторый момент времени τ : F(x, y, z,τ) :
v(x, y, z,t) t=τ |
= 0 |
||
∂v (x, y, z,t) |
(31) |
||
= F(x, y, z,τ) |
|||
∂t |
t |
=τ |
|
|
|
|
|
При этом τ становится параметром задачи. Иными словами воздействие внешней силы на объект заменяется на сообщение точкам объекта соответствующей скорости в некоторый
Теперь для решения задачи можно воспользоваться формулой (12) из §1, заменив в ней t на t −τ , тогда получим
v(x, y, z,t;τ) = t −τ |
F[x +αa(t −τ), y + βa(t −τ), z +γa(t −τ),τ]dσ1 ? |
(32) |
4πa ∫∫S |
|
|
|
1 |
|
Теперь покажем, что функция u(x, y, z,t) , определенная формулой |
|
|
|
t |
|
u(x, y, z,t) = ∫v(x, y, z,τ) dτ , |
(33) |
|
|
0 |
|
является решением неоднородного уравнения (28) при нулевых начальных условиях (29). Действительно,из формулы (33) находим
t
∆u(x, y, z,τ) = ∫∆v(x, y, z,τ) dτ
0
Дифференцируя теперь выражение (33) по времени,получим
∂u |
= t |
∂v(x, y, z,t;τ) |
dτ +v(x, y, z,t;τ) |t=τ , |
∂t |
∫ |
∂t |
|
|
0 |
|
|
(34)
(35)
причем внеинтегральный член при t =τ равен нулю в силупервого н ачального условия
(31), т.е.

|
|
|
|
∂u |
|
t |
∂v(x, |
y, z,t;τ) |
|
|
|
|
||
|
|
|
|
= ∫ |
dτ |
|
|
(36) |
||||||
|
|
|
|
∂t |
|
0 |
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференцируя ещё раз по t, будем иметь |
|
|
|
|
|
|
|
|||||||
∂2u |
t ∂2v(x, y, z,t;τ) |
|
∂v(x, y, z,t;τ) |
|t=τ |
|
|
||||||||
∂t |
2 |
= ∫ |
|
∂t |
2 |
|
|
dτ + |
|
∂t |
, |
(37) |
||
|
0 |
|
|
|
|
|
|
|
|
|
||||
причем здесь внеинтегральный член при |
t =τ |
в силу первого начального условия (31) |
||||||||||||
равен F(x, y, z,t) , т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2u |
t ∂2v(x, y, z,t;τ) |
|
|
|
|
|
||||||
|
|
∂t |
2 |
= ∫ |
|
|
∂t |
2 |
|
dτ + F(x, y, z,t) |
|
(38) |
||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
Поскольку функция v удовлетворяет уравнению (30), то (38) можно переписать следующим образом
∂22u |
= a2 |
t |
∫ vdτ + F(x, y,z,t), |
||
∂t |
|
0 |
а в силу(33) входящий в это выражениеинтеграл есть u. В итоге получим
∂2u = a2 u + F(x, y,z,t),
∂t2
т.е. функция u удовлетворяет исходному уравнению (28). При этом начальные условия
(29) также выполненыв силу(33) и (36).
Подставив в формулу(34) вместо функции v(x, y, z,t;τ)её выражение (32), получим
|
1 |
t |
|
|
|
|
|
|
|
F[x +αa(t −τ), y + βa(t −τ), z +γa(t −τ),τ]dσ |
|
|
|
u(x, y, z,t;τ) = |
|
∫ |
∫∫ |
1 |
|
|
4π |
||||||
|
|
(t −τ) |
|
dτ |
||
|
|
0 |
S1 |
|
|
|
Затем, если введем вместо τ новую переменную интегрирования r = a(t −τ) , то получим
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
||||
|
1 |
at 2π π |
F x +αr, y + βr, z +γr, t − |
|
|
|
||||||||||||
|
|
|
||||||||||||||||
u(x, y, z,t;τ) = |
∫ |
∫ ∫ |
|
|
|
|
|
|
|
a |
r2 sinθdθdϕdτ |
|
||||||
2 |
|
|
|
|
r |
|
|
|||||||||||
Вводя новые координаты |
4πa |
0 |
0 0 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ = x +αr, |
η = y + βr, |
|
ζ = z +γr |
|
|
|
|
||||||||||
И учитывая, что α2 + β2 +γ 2 =1, получим |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
r = |
(x −ξ)2 +(y −η)2 +(z −ζ )2 |
, |
|
|
|
|
|||||||||||
и выражение для u(x, y, z,t) окончательно запишется в виде |
|
|
|
|
||||||||||||||
|
|
|
|
|
1 |
|
g(ξ,η,ζ ,t − |
r |
) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||
u(x, y, z,t) = |
∫∫∫D |
|
|
|
a |
dξdηdζ |
(39) |
|||||||||||
4πa2 |
|
r |
|
|
||||||||||||||
|
|
|
|
|
|
|
at |
|
|
|
|
|
|
|
|
|
|
|
где Dat – шар радиуса at с центром в точке (x, y, z).
Выражение (39) называют запаздывающим потенциалом, так как при выполнения интегрирования функция g берется не в рассматриваемый момент времени t, а в момент,
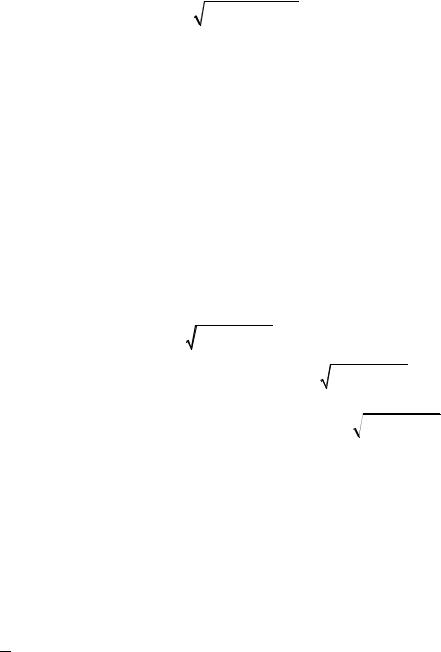
наступивший раньше на промежуток времени r/a, необходимый для того, чтобы возмущение, распространяясь со скоростью a от точки (ξ, η, ζ ), дошло до точки (x, y, z ).
Аналогичным образом мы можем получить решение для двухмерного волнового уравнения
∂2u |
= a |
2 |
∂2u |
+ |
∂2u |
|
|
(40) |
|||
∂t2 |
|
∂x2 |
∂y2 |
+ F(x, y,t) |
|
|
|||||
|
|
|
|
|
|
|
|||||
с нулевыми начальными данными |
|
|
|
|
|
|
|
|
|
|
|
|
u |t=0 = 0, |
|
|
∂u |
|t=0 = 0 |
|
|
(41) |
|||
|
|
|
|
|
|
∂t |
|
|
|
|
|
Это решение имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
t |
|
|
|
|
|
F(ξ,η,τ) |
|
|
|
u(x, y,t) = |
∫ |
∫∫ |
|
|
|
|
|
dξdηdτ |
(42) |
||
2πa |
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||||
|
0 ρ ≤a(t−τ ) a2 (t −τ)2 − ρ2 |
|
|
|
|||||||
где ρ2 = (x −ξ)2 +(y −η)2
§ 5. Точечный источник
Предположим, что свободный член в уравнении (28) отличен от нуля только в
небольшой сфере D с центром в начале координат. Тогда при стремлении радиуса этой сферы ε к нулю и при синхронном возрастании интенсивности внешней силы мы в пределе можем получить решение волнового уравнения для точечного источника,
который начинает действовать с момента t = 0по заданной зависимости от времени f (x, y, z, t).
Положим для определенности, что внутри сферы
∫∫∫ f (x, y, z,t) dx dy dz = 4πa2ω(t) , |
(43) |
|||
Dε |
|
|
||
считая по-прежнему |
|
|
||
|
|
|
||
f (x, y, z,t) = 0 при |
x2 + y2 + z2 |
≥ ε |
|
|
|
|
|||
Обратимся теперь к формуле (39) и будем считать, что at > |
x2 + y2 + z2 |
, при этом, |
||
очевидно, что достаточно произвести интегрирование по шару Dε. При ε → 0 величина r
будет равна расстоянию от начала координат до точки (x, y, z), т.е. r = 
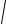 x2 + y2 + z2 , и мы получим, учитывая (43), что
x2 + y2 + z2 , и мы получим, учитывая (43), что
|
u(x, y, z,t) = |
1 ω(t − |
r |
) |
(at > 0) |
(44) |
|
|
|
||||||
|
|
r |
|
a |
|
|
|
Ясно, что при |
r > at u(x, y, z,t) = 0 , |
так |
как при |
r > at область |
интегрирования в |
||
интеграле (39) не содержит внутри себя шара Dε при достаточно малыхε. |
|||||||
Отметим, |
что при любом выборе |
функции |
ω(t) функция |
(44) удовлетворяет |
|||
уравнению (28) |
и представляет собой сферическую волну, расходящуюся радиально со |
||||||
скоростью а от начала координат. При этом воздействие на точку (x, y, z) в момент времени t зависит только от отдельного импульса, возникшего в начале координат в
момент времени t − ar и пришедшего в точку(x, y, z).
В случае уравнения (40) мы должны, также каки выше, считать, что

f (x, y,t) = 0 при 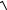
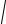 x2 + y2 ≥ ε ,
x2 + y2 ≥ ε ,
а вместо (43) написать
∫∫ f (x, y,t) dx dy = 2πa2ω(t) ,
Cε
где Сε – круг с центром в начале координат радиуса ε. |
|
|
||||
Обращаясь к формуле (42) и переходя к пределу при ε → 0, получим решение для |
||||||
точечного источника на плоскости |
|
|
|
|
||
t−ρ/a |
ω(t) |
|
|
|
||
u(x, y,t) = ∫ |
|
|
(at > ρ) |
(45) |
||
|
|
|
||||
a2 (t −τ)2 |
− ρ2 |
|||||
0 |
|
|
|
|||
где ρ = 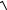
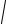 x2 + y2 и u(x, y,t) = 0 при at < ρ
x2 + y2 и u(x, y,t) = 0 при at < ρ
§ 6. Уравнения малых поперечных колебаний мембраны.
Теперь мы покажем, что малые поперечные колебания мембраны описываются двумерным волновым уравнением (1). Мембраной называют тонкую пленку, которая
находится в состоянии натяжения и не оказывает сопротивление изгибу и сдвигу. Покажем, что малые колебания мембраны описываются двумерным волновым уравнением.
Пусть бесконечная мембрана в положении равновесия расположена в плоскости (x,y) и находится под действием равномерного натяжения T, т.е. силы, приходящейся на
единицудлины произвольного контура и направленной перпендикулярно этому контурув каждой его точке. Будем также предполагать, что на мембрану параллельно оси 0u действует внешняя сила p( x, y, t), рассчитаннаяна единицуплощади.
Будем рассматривать только поперечные смещения мембраны, при которых каждая её точка движется перпендикулярно плоскости (x,y). Смещения u каждой точки мембраны
будут функцией координат этой точки x,y и времени t. Будем предполагать, что они настолько малы, что квадратами производныхux и uy можно пренебречь.
Выделим произвольный участок мембраны σ, ограниченный кривой l (Рис.3.1). В результате смещения этот участок деформируется и перейдет в некоторый участок σ ',
u |
|
ограниченный контуром |
l'. |
|
На |
этот |
|||||
|
участок в каждой его точке, в том числе и |
||||||||||
|
|
|
|||||||||
|
|
|
по контуру l' будет действовать |
||||||||
|
|
|
равномерно распределенное натяжение Т, |
||||||||
|
|
|
лежащее в плоскости касательной к |
||||||||
|
l' |
T |
поверхности мембраны. Сила этого |
||||||||
|
|
|
натяжения равна Тdl', где dl' – элемент |
||||||||
0 |
|
x |
дуги кривой l'. Проекция силы Тdl' на ось |
||||||||
|
|
0u будет равна абсолютной величине Тdl', |
|||||||||
|
|
||||||||||
|
|
|
умноженной на косинус угла вектора Т с |
||||||||
y |
n |
осью 0u, |
который |
в |
силу |
нашего |
|||||
предположения |
о |
малости |
величины |
||||||||
|
|
||||||||||
Рис.23. Вертикальное смещение участка мембраны |
смещения |
будет |
равен |
∂u |
, |
где |
n – |
||||
|
|
|
|
|
|
|
∂n |
|
|
|
|
внешняя нормаль к контуру l.
В результате равнодействующая сил, приложенныхкконтуру l' будет равна
