
Учебник по УМФ первая часть
.pdf
T ''(t) |
= |
X ''(x) |
|
a2T (t) |
X (x) |
||
|
В этом уравнении левая часть есть функция только переменной t, а правая – только переменной x. Это может иметь место, только если и левая и правая часть является
постоянной величиной, которую мы обозначим λ:
T ''(t) |
= |
X ''(x) |
= −λ |
(34) |
|
a2T (t) |
X (x) |
||||
|
|
|
где λ, может быть любым действительным числом и знак минус с этой точки зрения ничего не меняет, но для дальнейшего такое обозначения константы разделения оказывается более удобным. Заметим, что значение λ еще предстоит найти и только в том
случае если оно существует наше представление (33) оправданно. В связи с этим существование значения (или значений) числа λ называют условием разделения переменных.
Соотношение (33) позволяет нам записать два уравнения:
X ''(x) +λX (x) = 0 |
(35) |
T ''(t) + a2λT (t) |
(36) |
Чтобы функция (33), отличная от тождественного нуля, удовлетворяла нулевым граничным условиям (31), приходится потребовать, чтобы выполнялись условия
X (0) = 0 и X (l) = 0 |
(37) |
Таким образом, мы приходим к необходимости решить две задачи. Первая из них состоит в том, что требуется найти нетривиальное и ограниченное при всех x решение уравнения (35), удовлетворяющее граничным условиям (37), а также те значения λ, при
которых это решение существует. Эта двоякая задача носит название задачи ШтурмаЛиувилля. Найденные в результате решения задачи значения λ называются собственными
числами, а соответствующие им решения X (x) – собственными функциями.
Уравнение (35), как известно, имеет три вида решения в зависимости от того, какие корни имеет соответствующее характеристическое уравнение
k2 +λ = 0
В результате при λ = 0 учет нулевых граничных условий приводит к тривиальному решению, что противоречит условию задачи. При λ < 0 решение имеет вид
X (x) = C1e
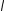 −λ x +C2e−
−λ x +C2e−
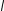 −λ x
−λ x
Подстановка первого граничного условия приводит к равенству C1 = −C2 , а
подстановка второго граничного условия приводит к равенству e−2l
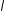 λ =1, чего не может быть, если λ ≠ 0 . Остается только случай λ > 0, тогда решение будет иметь вид
λ =1, чего не может быть, если λ ≠ 0 . Остается только случай λ > 0, тогда решение будет иметь вид
X(x) = C1 cos(
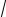 λ x) +C2 sin(
λ x) +C2 sin(
 λ x) ,
λ x) ,
Вкотором в силу первого граничного условия С1 = 0, а второе граничное условие приводит ксоотношению
|
|
|
|
|
X (l) = C2 sin( |
λl) |
= 0, |
откуда получаем λ |
= |
nπ 2 |
, где n= 1, 2, 3, . . ., ∞. |
||||
n |
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
В результате получаем бесконечный набор собственных чисел, каждому из которых соответствует собственная функция
X |
n |
(x) = C |
2n |
sin |
nπ x |
, |
(38) |
|
l |
||||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
где С2n – произвольные постоянные. Эта функция представляет собой с точностью до
множителя синус кратного аргумента
Теперь можно обратиться к решению уравнения (36). Поскольку мы имеем бесконечный набор значений λ, то вместо уравнения (36) нам предстоит решать
бесконечный набор уравнений одного вида
T |
n |
''(t) + a2λ |
n |
T (t) , |
где λ |
= |
nπ 2 |
(39) |
|||||
|
|
|
|
n |
|
|
n |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
При этихзначения λ уравнение (36) будет иметь решение |
|
||||||||||||
T |
(t) = A |
n |
cos(nπa t) + B |
n |
sin(nπa t) |
, |
(40) |
||||||
n |
|
|
|
|
l |
|
|
l |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
где An и Bn – произвольные постоянные, свои для каждого n. |
|
|
|
|||||||||||
В результате, перебирая значения n. мы получим бесконечный набор решений |
||||||||||||||
уравнения (33) следующего вида: |
|
|
|
|
|
|
|
|
|
|
||||
u |
n |
(x,t) = X |
n |
(x)T (t) =[A |
n |
cos ( |
nπa |
t) + B |
n |
sin ( |
nπa |
t)]sin |
nπ x |
(41) |
|
|
n |
|
l |
|
l |
|
l |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
При записи выражения (41) было учтено, что произведение произвольной константы C2n на произвольные константы An и Bn будет также давать произвольные константы, которые можно снова обозначить через An и Bn.
Сумма решений (41) и будет общим решением уравнения (33)
∞ |
∞ |
|
u (x,t) = ∑u n (x,t) = ∑Xn (x)Tn (t) |
(42) |
|
n=1 |
n=1 |
|
Каждая из функций un (x) представляет собой так называемую стоячую волну. Действительно, как мы уже отмечали, множитель sin(nπx/l) представляет собой
периодическую функцию по координате x с полупериодом, равным 1/n от длины струны, а множитель в квадратных скобках представляет собой периодическую по времени функцию
D sin(nπa t +γ |
n |
) , |
(43) |
|||||||
|
n |
|
l |
|
|
|||||
где Dn2= An2+Bn2 и γn=arctg (An |
|
/Bn), |
|
|
|
пропорциональным 1/n. Амплитуда |
||||
|
с периодом, |
|||||||||
колебания каждой точки с координатой x определяется по формуле |
||||||||||
H |
n |
= D |
sin( |
nπ |
x), |
(44) |
||||
|
|
|||||||||
|
n |
|
|
|
l |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
а частота по формуле |
|
|
|
nπa |
|
|
|
|
|
|
|
|
ωn = |
|
|
|
(45) |
||||
l
Стоячую волнус номером n называют n-ой гармоникой или n-ой модой колебаний.
На рис.18 приведены примеры графического изображения стоячих волн для n=1,2,3.
Константы An и Bn, а значит и константа Dn, представляющая собой амплитуду колебаний, остается пока неизвестной.
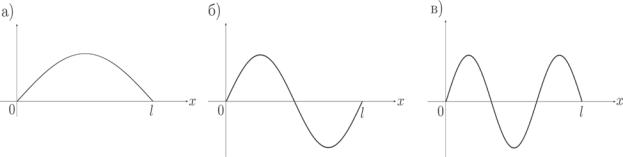
Рис. 18. Стоячие волны: а) n=1; б) n=2; в) n=3.
Теперь перейдем к определению констант An и Bn . Для этого воспользуемся начальными условиями (32), подставив полученное решение (42) с учетом (43). В
результате получим
|
∑An sin |
nπ x |
|
= f (x) |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
(46) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∑Bn |
nπa |
|
|
|
nπ x |
|
|
|
|
|
|
|
|
|
|||||||||||
|
sin |
|
= g (x) |
|
|
|||||||||||||||||||||
|
|
l |
|
|
l |
|
|
|
||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Умножим обе части на sin |
mπ x |
, |
проинтегрируем от нуля до l и воспользуемся |
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
соотношением ортогональности |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
l |
mπ x |
|
|
|
nπ x |
|
|
|
0 |
|
при m ≠ n |
|
||||||||||||||
∫sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
l |
sin |
|
|
|
l |
|
dx = l |
|
|
при m |
= n |
, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
l |
|
|
l |
|
|
|
|
|
nπ |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
An |
|
= ∫ f (x)sin( |
|
|
|
|
|
x)dx |
|
|
|||||||||||||
|
|
|
2 |
|
|
l |
|
|
|
|||||||||||||||||
после чего получим |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπa |
|
|
l |
|
|
|
|
|
|
|
|
nπ |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
= ∫g(x)sin( |
|
|
||||||||||||||||||
|
|
Bn |
2 |
|
|
|
|
|
|
x)dx |
|
|
||||||||||||||
|
|
|
|
|
|
|
l |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончательные выражениядлякоэффициентов An и Bn будут иметь вид |
||||||||||||||||||||||||||
|
A |
|
= |
2 l |
f (x)sin( |
nπ |
x)dx |
|
|
|||||||||||||||||
|
|
l ∫ |
|
|
|
|
||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(47) |
||
|
|
|
|
|
2 |
|
|
|
l |
|
|
|
|
|
|
nπ |
|
|
|
|||||||
|
B |
|
= |
|
|
|
g(x)sin( |
x)dx |
|
|
||||||||||||||||
|
|
|
|
|
|
|
∫ |
|
|
|
||||||||||||||||
|
n |
|
|
nπa |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, решение задачи о малых поперечных свободных колебаниях ограниченной струны, защемленных на обоих концах, имеет вид суперпозиции бесконечного набора стоячих волн, которые определяются по формуле (41) с учетом формул (47).
Замечание о колебании музыкальных струн
Колеблющаяся струна возбуждает колебания окружающего воздуха, воспринимаемые ухом человека как звук. Музыкальные звуки принято располагать в
порядке возрастания частоты колебаний, создаваемых музыкальным инструментом, от низких к высоким. Колебание музыкальной струны с самой малой (низкой) из её частот называют основным тоном. Колебания той же струны с частотами ωn, кратными

основному тону, называют обертонами. Изменение основного тона струны производится изменением её натяжения Т, а значит и коэффициента a = 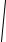 Tρ в формуле (45), или длины
Tρ в формуле (45), или длины
струны l. Другая возможность изменения звука связана, как мы видим, с изменением
линейной плотности ρ, т.е. с переходом на другую струну. Следует заметить, что амплитуды колебаний с увеличением номера гармоники весьма быстро уменьшаются. В
связи с этим именно основной тон той нотой, на которую настроена струна, а действие обертонов определяет тембр звука.
Среди струнных музыкальных инструментов различают три типа: щипков ые (арфа,
гитара, мандолина), ударные (рояль) и смычковые (скрипка, виолончель). Они отличаются друг от друга способом возбуждения колебаний струны. В щипковых инструментах
возбуждение струны происходит за счет отклонение струны из состояния покоя, после чего струна колеблется и издаёт звук, весьма короткий. В ударных струнных инструментах возбуждение струны происходит за счет придание струне некоторой
первоначальной скорости (без начального отклонения) за счет удара молоточка. В смычковых инструментах возбуждение струны происходит за счет быстрой
последовательности отклонений струны за счет силы трения между струной и движущимся смычком. Этой силы хватает лишь на небольшое смещение струны, после чего струна освобождается и звучит короткое время, но в результате уменьшения
амплитуды колебаний силы трения уже следующего участка смычка оказывается достаточно, чтобы вновь «заставить»её звучать. Так удается продлить звучания струны на
время движения смычка, в результате чего смычковые инструменты могут издавать продолжительный звук.
§ 7. Вынужденные колебания струны, закрепленной на концах
Рассмотрим вынужденные колебания однородной струны, закрепленной на концах, под действием внешней силы p (x, t), рассчитанной на единицу длины. В этом случае
колебания струны будут описываться неоднородным уравнением
u −a2u |
xx |
= F(x,t), |
(48) |
tt |
|
|
где F(x,t) = ρ1 p (x,t)
при нулевыхграничныхусловиях
u(0,t) = 0 u(l,t) = 0
и начальныхусловияхобщего вида
u(x,0) = f (x) ut (x,0) = g(x)
Будем искать решение этой задачи в виде суммы u(x,t) = v(x,t) + w(x,t)
где v (x, t) есть решение такого же неоднородного уравнения, что и (45) vtt −a2vxx = F(x,t)
с теми же граничными условиями, что и (46)
(49)
(50)
(51)
(52)

v(0,t) = 0 , v(l,t) = 0,
но с нулевыми начальными условиями
v (x,0) = 0 , vt (x,0) = 0
а w(x, t) есть решение однородного уравнения
wtt = a2w x x ,
удовлетворяющее тем же нулевым граничным условиям
w(0,t) = 0 , w(l,t) = 0
и начальными условиями
w(x,0) = f (x) wt (x,0) = g(x)
(53)
(54)
(55)
(56)
(57)
Решение w(x, t) представляет свободные колебания струны, т.е. такие колебания, которые происходят только вследствие начального возмущения струны. Решение же v (x,t) представляет собой вынужденные колебания, т.е. колебания, которые происходят под действием внешней возмущающей силы, когда начальное возмущение струны отсутствует. Вообще говоря, для того, чтобы такие колебания имели место надо, чтобы
внешняя сила была периодической. Однако предлагаемый метод решения уравнения (48) рассчитан на произвольное изменение вовремени силы p (x, t).
Метод нахождения свободных колебаний, описываемых однородным уравнением (52) был изложен выше (§ 6), так что мы остановимся только на нахождении решения неоднородного уравнения (52). Как и в случае свободных колебаний будем искать
решение v в виде ряда
∞ |
|
|
v(x,t) = ∑Tn (t)sin nπ x |
(58) |
|
n=1 |
l |
|
|
|
|
В этом случае нулевые граничные условия будут выполняться сами собой.
Определим теперьфункции Tn (t) так, чтобы ряд (58) удовлетворял уравнению (52) и начальным условиям (54). Подставив ряд (58) в уравнение (52), получим
∞ |
|
|
|
∑[Tn ''(t) +ωn2Tn (t)]sin nπ x |
= F(x,t), |
(59) |
|
n=1 |
l |
|
|
|
|
|
|
где ω= nπl a .
Теперь разложим функцию F (x,t)в ряд Фурье по синусам в интервале (0, l):
|
|
∞ |
|
|
|
F(x,t) = ∑Fn (t)sin nπ x |
, |
(60) |
|||
|
n=1 |
l |
|
|
|
где |
|
|
|
||
|
|
|
|
|
|
F (t) = |
2 l |
F(ξ,t)sin nπξ dξ |
|
||
n |
l ∫ |
|
l |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Сравнивая разложения (59) и (60) |
для |
одной и той |
же функции |
F (x,t), получим |
|
бесконечный набор обыкновенных дифференциальных уравнений для определения функций Tn (t).
T |
n |
''(t) +ω2T (t) = F (t) |
|
(n = 1,2,3,…), |
(61) |
|||||||
|
|
|
n |
n |
n |
|
|
|
|
|
|
|
Чтобы решение v (x, t), определяемое рядом (58) удовлетворяло начальным |
||||||||||||
условиям (54) надо потребовать, чтобы все Tn (t) удовлетворяли условиям |
|
|||||||||||
Tn (0) = 0 |
|
u |
Tn '(0) = 0 |
(n = 1,2,3,…) |
(62) |
|||||||
Решение уравнений (62) с начальными условиями (63) имеет известный из курса |
||||||||||||
обыкновенныхдифференциальных уравнений вид: |
|
|
|
|
|
|
||||||
|
T |
(t) = |
1 |
t |
F (τ)sin ω |
|
(t −τ)dτ |
(63) |
||||
|
ωn |
∫ |
|
|||||||||
|
|
n |
|
n |
|
n |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
o |
|
|
|
|
|
|
|
или, подставляя вместо Fn (t) из формулы (58) |
и внося sin |
nπ |
x под знак интеграла, |
|||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
l |
|
|
получим окончательное выражение для Tn(t) в следующем виде:
T (t) = |
2 t l |
F(ξ,τ)sin ω |
|
(t −τ)sin nπ |
ξ sin nπ x dξdτ |
(64) |
|
|
|
|
|||||
nπa ∫∫ |
|
||||||
n |
|
n |
l |
l |
|
||
|
|
|
|
|
|
||
o o
Подставив найденные выражения для Tn(t) в ряд (58), получим решение задачи (52) – (54), а именно
v (x,t) = |
2 t l ∞ 1 |
F(ξ,τ)sin ωn (t −τ)sin nπξ sin nπ |
x dξdτ |
(65) |
|||||||
|
|
||||||||||
πa ∫∫∑n |
|||||||||||
|
|
|
|
l |
l |
|
|
|
|||
|
|
o o n=1 |
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t l |
|
|
|
|
|
|
||
|
|
v (x,t)=∫∫G(x,ξ,t −τ) F(ξ,τ) dξdτ , |
|
|
(65') |
||||||
|
|
|
0 0 |
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
G (x,ξ,t −τ) = |
2 |
|
∞ 1 sinωn (t −τ)sin nπ |
xsin nπ |
ξ |
|
|||||
πa |
|
||||||||||
|
|
|
∑n |
l |
|
l |
|
|
|||
|
|
|
|
|
n=1 |
|
|
|
|
|
|
§ 8 . Продольные колебания однородного стержня
Стержнем называют тело, один из размеров которого, называемый продольным, значительно превышает его размеры в плоскости, перпендикулярной к продольному
направлению, т.е. поперечные размеры. Основным свойством стержня является сопротивление, оказываемое продольному сжатию (растяжению) и изгибу. Это свойство
коренным образом отличает стержень от струны, которая не растягивается и не сопротивляется изгибу. Если плотность материала стержня во всех его точках одинакова, то стержень называют однородным.
Обычно в качестве стержней рассматриваются протяженные тела, ограниченные замкнутой цилиндрической поверхностью. В этом случае площадь поперечного сечения
остается постоянной. Мы будем изучать поведение именно такого однородного стержня длины l, предполагая, что он подвержен только сжатию или растяжению, подчиняясь при этом закону Гука. При изучении малых продольных деформаций стержня обычно принимается так называемая гипотеза плоских сечений. Она заключается в том, что поперечные сечения, перемещаясь при сжатии или растяжении вдоль стержня, остаются плоскими и параллельными друг другу.

Направим ось x вдоль продольной оси стержня (Рис. 19) и будем считать, что в начальный момент времени концы стержня находятся в точках x=0 и x=l. Возьмем произвольное сечение стержня с координатой x. Обозначим через u (x, t) смещение этого
|
|
|
u |
|
u + du |
|
сечения в момент времени t, тогда смещение |
||||
|
|
|
|
|
сечения с координатой |
x + dx в тот же момент |
|||||
|
|
|
|
|
|
|
|
времени будет равно |
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x |
|
δu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
dx |
|
l |
u + du = u + δ x dx |
|
|||||
|
|
|
|
||||||||
|
|
x |
x + dx |
|
Тогда относительное удлинение стержня в |
||||||
|
|
|
сечении x будет равно |
|
|||||||
Рис. 19. Смещение сечений стержня |
|
|
|
∂u(x,t) |
|||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
Сила сопротивления этому удлинению по законуГука будет равна |
|||||||||
|
|
|
|
|
|
|
T = ES |
∂u , |
(66) |
||
|
|
|
|
|
|
|
|
∂x |
|
||
где E – модуль упругости материала стержня (модуль Юнга), а S – площадь поперечного сечения. На границах участка стержня длиной dx на него действуют силы Tx и Tx+dx ,
направленные вдоль осиx. Результирующая эти ихсил будет равна
|
∂u |
∂u |
∂2u |
|
Tx+dx −Tx = ES |
∂x x+dx −ES |
∂x x = ES |
∂x2 |
, |
а ускорение рассматриваемого участка стержня равно ∂2u , тогда уравнение движения
∂t2
этого участка стержня будет иметь вид:
ρSdx |
∂2u |
= ES |
∂2u |
dx, |
(67) |
||
∂t |
2 |
∂x2 |
|||||
|
|
|
|
||||
где ρ – плотность материала стержня. Если эта плотность и модуль Юнга, постоянны , то
можно ввести величинуa = |
|
E |
|
через и, поделив обе части уравнения на Sdx, |
|
ρ |
|||||
|
|
|
|
окончательно получить уравнение продольных колебаний стержня в отсутствии внешних сил
∂2u |
= a2 ∂2u dx |
(68) |
∂t2 |
∂x2 |
|
Это уравнение по форме совпадает с уравнением поперечных колебаний струны и
методы решения для него те же, однако, коэффициентом a в этих уравнениях обозначены разные величины. В уравнении струны величина a2 представляет дробь, в числителе
которой стоит постоянная сила натяжения струны – Т, а в знаменателе линейная плотность ρ, а в уравнении струны в числители стоит модуль Юнга, а в знаменателе – объемная плотность материала стержня ρ. Отсюда и физический смысл величины a в этих уравнениях разный. Если для струны этот коэффициент является скоростью распространения малого поперечного смещения, то для стержня он является скоростью
распространения малого продольного растяжения или сжатия и называется скоростью распространением звука, поскольку именно с этой скоростью будут распространяться по стержню малые продольные колебания, представляющие собой звук.

Для уравнения (68) задаются начальные условия, которые определяют смещение и скорость смещения любого сечения стержня в начальный моментвремени:
u(x,0) = f (x) |
(69) |
||
ut (x,0) |
= g(x) |
||
|
|||
Дляограниченного стержня задаются условиязакрепленияили приложениясилы на его концахв виде граничныхусловий 1-го, 2-го и 3-го рода.
Граничные условия первого рода задают продольное перемещение на концах стержня:
u(0,t) =η1 |
(t) |
(70) |
|
u(l,t) =η2 (t) |
|||
|
|||
Если концы стержня закреплены неподвижно, то в условиях (6) η1 (t) =η2 (t) = 0 . В этом
случае, так же как и в задаче о колебании защемленной струны применим метод
разделения переменных.
В граничных условиях II рода на концах стержня задаются упругие силы,
образующиеся в результате деформации по закону Гука в зависимости от времени. Согласно формуле (66) эти силы с точностью до постоянного множителя равны производной ux, поэтомуна концахи задаются эти производные как функции времени:
ux (0,t) =φ1(t) u x(l,t) =φ2 (t)
Если один из концов стержня свободен, то наэтом конце ux = 0. Граничные условия третьего рода могут быть представлены
(71)
как условия, при
которых к каждому концу стержня прикреплена пружина, другой конец которой перемещается вдоль оси по заданномузакону времени θ (t), как это изображено на Рис. 20. Эти условия могут быть записаны следующим образом
u |
x |
(0,t) = |
|
k1 |
[u(0,t) −θ (t)] |
|
|
|
|
|
|||||
|
|
|
ES |
1 |
|
||
|
|
|
|
, |
(72) |
||
|
|
|
|
k2 |
|||
u x(l,t) = |
|
[u(l,t) −θ2 (t)] |
|
||||
ES |
|
||||||
|
|
|
|
|
|
||
где k1 и k2 – жесткости пружин.
θ1(t) |
|
θ2(t) |
0 |
l |
x |
|
Рис.20. Иллюстрацияграничных условий третьего рода
Если на стержень вдоль оси действует ещё и внешняя сила p (x, t), рассчитанная на единицуобъема, то вместо уравнения (50) следует записать неоднородное уравнение
ρSdx ∂2u = ES ∂2u dx + p(x,t)Sdx ,
∂t2 ∂x2
Которое, после деления на ρSdx примет вид

|
|
∂2u |
−a2 ∂2u |
= F(x,t), |
(73) |
||
|
|
∂t2 |
|
∂x2 |
|
|
|
где F(x,t) = |
1 |
p (x,t) . Уравнение (73) |
представляет собой |
уравнение вынужденных |
|||
ρ |
|||||||
|
|
|
|
|
|
||
продольных колебаний стержня, которое решается по аналогии с уравнением вынужденныхколебаний струны.
Замечание. Следует заметить, что и струна и стержень являются моделями реальных тел, которые в действительности могут проявлять как свойства струны, так и
стержня, в зависимости от условий, в которых они находятся. Кроме того, в полученных уравнениях не учитываются силы сопротивления окружающей среды и силы внутреннего
трения, в результате чего эти уравнения описывают незатухающие колебания. Для учета эффекта затухания в простейшем случае используется диссипативная сила, пропорциональная скорости и направленная в сторону, противоположную движению, т.е.
скорости. В результате уравнение (73)принимает вид
∂2u |
−a2 ∂2u |
+b |
∂u |
= F(x,t) |
(74) |
∂t2 |
∂x2 |
|
∂t |
|
|
§ 9. Случай ненулевых граничных условий.
Уравнение колебания струны и уравнение колебания стержня суть одномерные
волновые уравнения с разным физическим смыслом. Изложенный выше метод разделения переменных для однородных уравнений требовал, чтобы граничные условия были нулевыми. В случае ненулевых граничных условий
u(0,t) = µ1(t) |
|
u(l,t) = µ 2(t) |
(75) |
искомое решение u(x,t) имеет смысл искать в виде суммы двух слагаемыхu1 и u2, выбрав в качестве u1
u1(x,t) = µ1(t) + xl [µ2 (t) − µ1(t)]
Тогда вторую часть u2(x,t) можно искать какрешение уравнения с нулевыми граничными условиями:
u2 |
(0,t) = 0 |
(76) |
|
u2 |
(l,t) = 0 |
||
|
|||
При этом сумма двух частей будет |
удовлетворять уравнению с неоднородными |
||
граничными условиями . |
|
|
|
§ 10. Телеграфное уравнение.
Как известно, при прохождении электрического тока по проводнику, вокруг него образуется электромагнитное поле, которое в свою очередь вызывает изменения, как силы
тока, так и величины напряжения. В результате в проводнике возникает определенный колебательный процесс, который мы постараемся описать уравнениями в частных производных.

Совместим ось x с осью проводника длиной l, поместив начало координат в один из его концов. Сила тока I и напряжение v в каждой точке проводника будут функциями координаты x и времени t. Выведем уравнения с частными производными, связывающие
эти величины между собой. Будем предполагать, что емкость С, сопротивление R, самоиндукция L и утечка G, которая имеет место за счет несовершенства изоляции,
распределены вдоль провода непрерывно, равномерно и рассчитаны на единицу длины проводника.
Применяя закон Ома к участку проводника, заключенного между двумя произвольными сечениями с координатами x1 и x2, мы получим
|
|
|
|
|
x |
x |
|
|
v(x1,t) −v(x2,t) = R ∫2 i(x,t)dx + L ∫2 ∂i(x,t)dx |
(77) |
|||||||
|
|
|
|
|
x |
x |
∂t |
|
С другой стороны |
|
|
|
|
1 |
1 |
|
|
|
|
|
,t) = −x2 ∂v(x,t)dx |
|
||||
v(x |
,t) −v(x |
(78) |
||||||
1 |
|
|
2 |
|
|
x∫ ∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
Вычитая из первого равенства второе, получим |
|
|
||||||
|
x2 |
∂v |
+ L |
∂i |
|
|
|
|
|
|
|
|
+ Ri dx = o |
|
|
||
|
x∫ |
∂x |
|
|
∂t |
|
|
|
|
1 |
|
|
|
|
|
|
|
Откуда в силупроизвольности интервала интегрирования следует, что |
|
|||||||
|
∂v + L |
∂i + Ri = 0 |
|
(79) |
||||
|
∂x |
|
∂t |
|
|
|
||
Количество электричества, протекающего через рассматриваемый участок проводника за единицувремени равно
i(x1,t) −i(x2,t) = −x∫2 ∂∂xi dx
x1
С другой стороны оно равно сумме электричества, необходимого для зарядки этого участка, и электричества, которое теряется вследствие несовершенства изоляции, т.е.
|
|
|
x |
|
|
|
x |
|
|
|
|
|
C ∫2 |
∂v dx +G ∫2 v dx |
|
||||||
|
|
|
x |
|
∂t |
|
x |
|
|
|
|
|
1 |
|
|
1 |
|
||||
В результате сравнения этихвыражений получим |
|
|
||||||||
x2 |
∂i |
|
|
∂v |
|
|
|
|||
x∫ |
|
|
|
|
+C |
|
+Gv |
dx = o, |
|
|
∂x |
∂t |
|
||||||||
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
откуда |
∂i |
+C ∂v +Gv = 0 |
|
|||||||
|
(80) |
|||||||||
|
|
|||||||||
|
∂x |
|
∂t |
|
|
|
||||
Таким образом, линейные уравнения в частныхпроизводныхпервого порядка (79) и (80) описывают свободные электрические колебания в проводнике.
