
Учебник по УМФ первая часть
.pdfто разность между первоначальным решением u (x,t) и новым решением u1 (x,t) будет по абсолютной величине меньше ε на любом конечном отрезке времени, что легко следует из формулы (19).
Частные случаи
Рассмотрим два частныхслучая начальных условий.
1) Н а ч а л ь н ы е с к о р о с т и т о ч е к с т р ун ы р а в н ы н ул ю, а начальное смещение имеет место лишь в конечном промежутке (– b, b). В этом случае формула (19)
будет иметь вид:
u (x,t) = 12 [ f (x −at) + f (x + at)]. |
(20) |
Решение (20) представляет собой сумму двух волн, распространяющихся влево и вправо со скоростью a, причем начальная форма обеих волн определяется функцией f(x)/2, т.е. равной половине первоначального смещения струны.
Пусть, в частности, начальное смещение неограниченной струны, материал которой таков, что a =1, задается следующим образом:
u(x,0) |
1, |
x [−1,1], |
= f (x) = |
x (−∞, −1) (1, +∞), |
|
|
0, |
|
Тогда, пользуясь формулой (20), |
мы можем выписать выражения для смещения струны в |
|
моменты времени t = |
1 |
,1, 2,3 . |
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Для t = 1 |
мы получим: |
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
1 |
, |
3 |
|
, |
|
|
|
|
1 |
1, |
− |
2 |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
f x − |
|
= |
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
2 |
|
0, |
x |
|
−∞, − |
||||||||
|
|
|
|
|
|
|
, +∞ . |
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
3 |
, |
1 |
|
, |
|
|
|
1 |
1, |
x − |
2 |
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
f x + |
2 |
|
= |
|
|
|
|
|
|
3 |
1 |
|
|
|
|
|
0, |
−∞, − |
|||||||||
|
|
|
|
x |
|
|
|
, +∞ . |
|||||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
, |
|
|
|
3 |
, |
− |
1 |
|
, |
|
|
||
|
|
|
|
2 |
x − |
2 |
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1, |
|
x |
− |
1 , |
1 , |
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
u x, |
2 |
|
= |
1 |
|
|
1 |
|
3 |
|
|
|
|
|
|
|
||
|
|
|
, |
|
, |
, |
|
|
|
|
||||||||
|
|
|
|
2 |
x |
2 |
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
−∞, − |
|
||||||||||
|
|
|
0, |
|
x |
|
2 |
|
|
2 |
, +∞ . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для t =1: |
|
|
|
|
|
f (x −1) |
1, |
x [0,2], |
f (x +1) |
1, |
x [−2,0], |
= |
x (−∞,0) (2, +∞). |
= |
x (−∞, −2) (0, +∞). |
||
|
0, |
|
0, |

1 , u (x,1)= 2
0,
Для t = 2:
x [−2,2],
x (−∞, −2) (2, +∞).
f (x −2) |
1, |
x [1,3], |
f (x + 2) |
1, x [−3, −1], |
|
= |
x (−∞,1) (3, +∞). |
= |
x (−∞, −3) (−1, +∞). |
||
|
0, |
|
0, |
||
Для t = 3: |
|
f (x −3) |
1, |
= |
|
|
0, |
|
, |
[ |
|
] |
|
|
1 |
x |
−3, −1 [1,3], |
||||
u (x,2)= 2 |
|
x (−∞, −3) (3, +∞). |
||||
|
|
|||||
0, |
|
|||||
x [2,4], |
|
f (x +3) |
= |
1, x [−4, −2], |
||
x (−∞,2) (4, +∞). |
|
x (−∞, −4) (−2, +∞). |
||||
|
|
|
0, |
|||
1 , x [−4, −2] [2,4], u (x,3)= 2
0, x (−∞, −4) (4, +∞).
2) Н а ч а л ь н о е с м е щ е н и е р а в н о н у л ю, а функция g(x) отлична от нуля
лишь в ограниченном промежутке (– b, b). В этом случае говорят, что струна имеет только начальный импульс, а решение (19)принимает вид:
|
|
|
|
|
|
|
1 |
|
x |
+at |
|
|
|
|
|
|
|
||
|
|
u (x,t) = |
|
|
∫ |
g(ς) dς , |
|
|
(21) |
||||||||||
|
|
2a |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
x−at |
|
|
|
|
|
|
|
|||||
или полагая: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫g(ς) dς =Φ(x) , |
|
|
|
|
||||||||||||
|
|
|
a |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
можем записать: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x+at |
ς |
|
ς |
= Φ |
(x |
+ |
at) |
− |
Φ |
(x |
− |
at)] |
. |
||||||
a |
∫ g( ) d |
|
[ |
|
|
|
|
|
|
|
|||||||||
x−at |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда окончательно получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u (x,t) |
= |
1 |
Φ |
(x |
+ |
at) |
−Φ |
(x |
− |
at)] |
. |
(22) |
|||||||
|
2 |
[ |
|
|
|
|
|
|
|||||||||||
Отсюда видно, что и в этом случае по струне будут распространяться две волны – одна прямая и одна обратная. Результат их прохождения будет следующим. При t < x b−b
промежуток интегрирования в формуле (21) не будет иметь общих точек с интервалом (– b, b), а значит функция g(x) будет равна нулю (струна покоится). Начиная с момента
времени |
t = |
x −b |
промежуток интегрирования в формуле (21) будет накладываться на |
||||||
|
|||||||||
|
|
b |
|
|
|
|
x −b |
|
|
интервал |
(– b, |
b) и точка x начнет смещаться. Наконец, |
при |
t > |
промежуток |
||||
b |
|||||||||
|
|
|
|
будет целиком содержать интервал (–b, b) |
|
|
|
||
интегрирования |
|
и |
интегрирование будет |
||||||

сводиться к интегрированию по этому интервалу, так как вне его g(x) = 0, т.е. при t > x b−b смещение u (x, t) будет иметь постоянное значение d, определяемое интегралом:
d = 21a −∫bb g(ς) dς .
Таким образом, действие первоначального импульса приводит к тому, что с
течением времени точки струны смещаются на отрезок d и остаются без движения в этом новом положении. Иначе говоря, волны оставляют после себя постоянный след своего
прохождения.
Пусть, в частности, начальное смещение неограниченной струны равно нулю, а начальная скорость задается следующим образом:
ut (x,0) |
a, x [0, h], |
|
= g(x) = |
x (−∞,0) (h, +∞). |
|
|
0, |
|
Тогда, пользуясь формулой (21) и (22), мы можем выписать выражения для смещения струны в любой момент времени.
Имея в виду, что интеграл с переменным верхним пределом от заданной функции g определяется выражением
χ |
0, |
при χ < 0, |
|
|
при χ [0, h], |
∫g(ς) dς = aχ, |
||
0 |
|
χ > h. |
|
ah, |
|
для Φ(x + at) |
и Φ(x −at) получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при x+ at < 0, |
|
|
|
|
|
|
|
|
|
|
|
при x−at < 0, |
|
|
|
|
|
|||||||||||||
|
|
0, |
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
||||||||||||||||||
Φ(x + at) |
|
1 |
(x + at), |
|
|
при x+ at [0, h], |
|
Φ(x −at) = |
|
1 |
(x |
−at), |
|
при x−at [0, h], |
|
|
|||||||||||||||||||||
= |
2 |
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
h |
, |
x + at > h. |
|
|
|
|
|
|
|
|
h |
, |
|
|
x −at > h. |
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В частности, для |
t = |
h |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
при x < − |
h |
, |
|
|
|
|
|
|
|
|
|
|
|
при x < |
h |
, |
|
|
|
|
|
||||||||||
|
|
0, |
|
2 |
|
|
|
|
|
|
|
|
0, |
|
2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
h |
1 |
|
h |
|
|
|
|
|
|
|
h |
|
h |
|
|
h |
|
1 |
|
|
h |
|
|
|
h |
|
3h |
|
|
|||||||
|
|
, |
|
при x |
, |
, |
|
|
|
, |
|
, |
, |
||||||||||||||||||||||||
Φ x + |
|
= |
2 |
x + |
2 |
|
|
− |
2 |
|
Φ x − |
|
= |
2 |
x − |
2 |
|
при x |
2 |
2 |
|
||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
h |
, |
x > |
h |
. |
|
|
|
|
|
|
|
|
|
|
h |
, |
x > |
3h |
. |
|
|
|
|
|
|
||||||||||
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

u x,
Для t = ah :
|
|
|
|
|
при x < − |
h |
, |
|
|
|
|
|
|
|
|||||
|
|
0, |
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
h |
|
|
|
|
|
|
h |
|
h |
|
||||
|
|
|
|
|
при x |
|
, |
, |
|||||||||||
h |
|
2 |
x + |
2 |
, |
− |
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||
|
|
= |
|
x |
|
3h |
|
|
|
|
h |
|
3h |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||||
2a |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
− |
|
+ |
|
|
, |
при x |
|
, |
|
|
|
, |
|
|||
|
|
2 |
|
4 |
2 |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
3h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x > |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0, |
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
при x < −h, |
0, |
|
||
|
1 |
(x + h), при x |
|
Φ (x + h)= |
2 |
||
|
|
|
|
h |
, |
x > 0. |
|
|
2 |
||
|
|
|
|
и тогда
u x,
Для t = 2ah :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при x < h, |
|
|
|
|
|
0, |
|
||
[−h,0], |
|
|
1 |
(x −h), при x [h,2h], |
||||
|
Φ (x −h)= |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
, |
x > 2h. |
|
|
|
|
|
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|
0, |
|
при x < −h, |
|
|
|
||
|
|
1 |
(x + h), |
при x [−h,0], |
|
|||
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
h |
h |
, |
при x (0, h], |
|
|
|
||
|
= |
2 |
|
|
|
|||
a |
|
x |
|
|
|
|
|
|
|
− |
+ h, |
при x (h,2 h], |
|
|
|||
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
x > 2h. |
|
|
|
|
|
0, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при x < −2h, |
0, |
|
||
|
1 |
(x + 2h), при |
|
Φ (x + 2h)= |
2 |
||
|
|
|
|
h |
, |
x > −h. |
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
при x < 2h, |
|
0, |
|
||
x [−2h, −h], |
|
1 |
(x −2h), при x [2h,3h], |
|
Φ (x −2h)= |
2 |
|||
|
|
|
|
|
|
h |
, |
x > 3h. |
|
|
|
2 |
||
|
|
|
|
|
u x, 2ah
|
0, |
|
при x < −2h, |
|
||
|
|
x |
|
+ h, при x [−2h, −h], |
||
|
|
|
||||
|
2 |
|||||
|
|
|
|
|
|
|
|
h |
, |
при x (−h,2 h], |
|||
|
= |
2 |
|
|||
|
|
|
x |
+ 3h , при x |
|
|
|
− |
(2h,3h], |
||||
|
|
|||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
x > 3h. |
|
|
0, |
|
|
|||
|
|
|
|
|
|
|
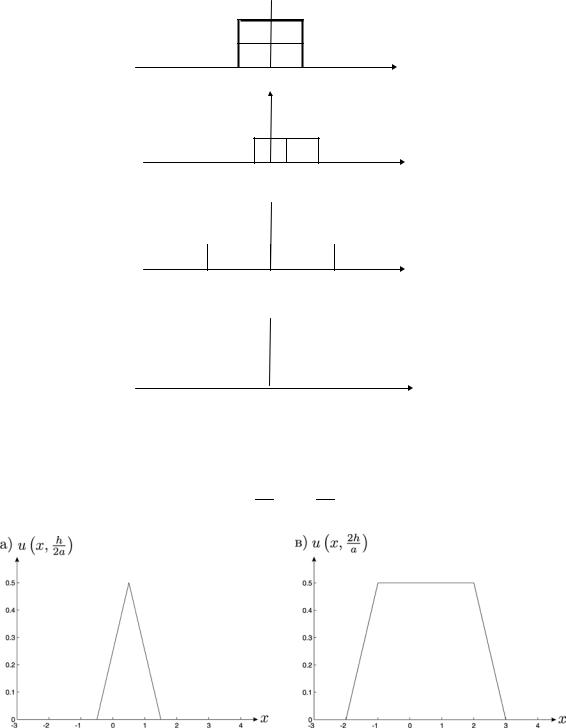
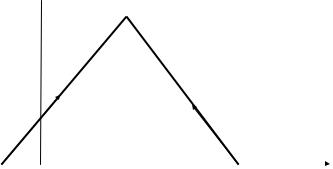
Графическая интерпретация
Первый частный случай имеет простую графическую интерпретацию. На рис. 12.
показано, как начальное смещение расщепляется на две полуволны, движущиеся в противоположныхнаправлениях.
Приведенная схема может служить графическим способом построения решения задачи Коши с нулевой начальной скоростью.
u 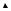
–1 u |
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
1 |
|
x |
u 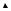
|
|
|
–1 |
1 |
x |
u 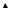
|
|
|
|
|
–1 |
1 |
x |
||
Рис. 12.Графическаяиллюстрацияпервого частного случая.
Для второго частного случая на рис. 14 приведены графики полученного смещения в случае a =1, h =1 в моменты времени t = 2ha и t = 2ah
Рис. 13. Графическаяиллюстрация второго частного случая.
§ 4. Метод характеристик
Ещё один способ решения задачи Коши можно получить исходя из
пространственно-временной интерпретации формулы Даламбера. Сначала рассмотрим 1-й частный случай, когда начальная скорость точек струны равна нулю. В этом случае
решение определяется формулой (20)
u (x,t) = 1 |
[ f (x −at) + f (x + at)] |
2 |
|
Из этой формулы следует, что функция f остается постоянной, если сохраняют свое |
|
значение выражения x – at или x + at , |
т.е. x – at = c1, x + at = c2 . На плоскости (x, t) эти |
выражения представляют собой уравнения прямых, называемых характеристиками волнового уравнения (Рис. 14).
t 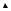 u (x0 , t0)
u (x0 , t0)
x + at = x0 + at0
x – at = x0 – at0
(x0 – at0,0) |
(x0 + at0,0) |
x |
|
Рис. 14. Характеристики одномерного волнового уравнения
Вдоль указанных прямых функция f сохраняет своё значение, которое она имела на
оси x т.е. в начальный момент времени, а совокупность этих знач ений нам известна как начальное смещение струны. Таким образом, решение задачи Коши для уравнения колебания струны для любой точки плоскости (x, t) можно получить, проведя через неё
две характеристики, уравнения которыхбудут
x −at = x0 −at0 x + at = x0 + at0
и взяв полусумму значений функции f, которые она имеет на этиххарактеристиках. Используя такую интерпретацию формулы Даламбера, решим задачу,
сформулированную в предыдущем параграфе, а именно
u(x,0) =1 в интервале x (−1, 1)и 0 вовсехостальныхточках ut (x,0) = 0
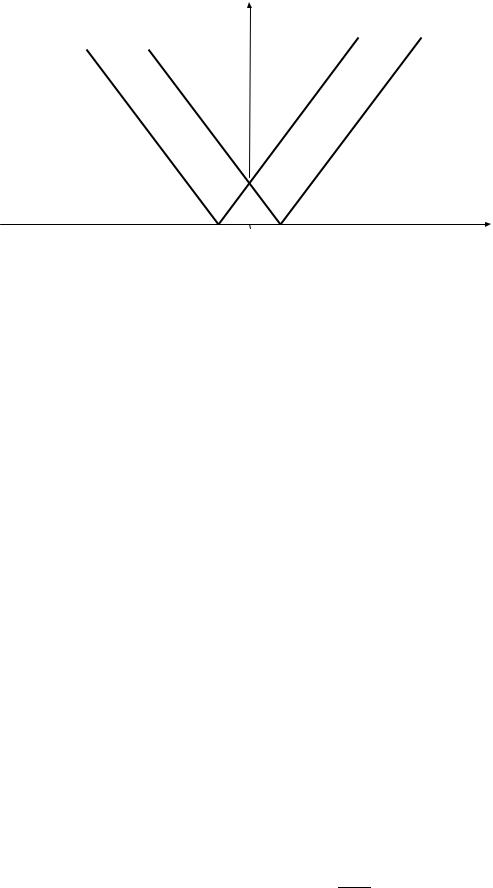
На рис. 15 решение задачи изображено в плоскости переменных x, t , ане u, x как в
предыдущем параграфе. Всё полупространство получается разбитым на 6 областей. В трех из нихрешение равно нулю, в двух– одной второй и в одной – единице.
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|||
x + at = – 1 |
|
|
x + at = 1 |
|
|
|
x – at = – 1 |
|
|
|
x – at = 1 |
|||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
u = 0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
||||
|
|
|
|
|
u = 1/2 |
|
u = 1/2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = 0 |
|
|
|
|
|
|
|
|
|
|
|
u = 0 |
|
|||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
u =1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
–1 |
0 1 |
|
|
|
|
|
|
x |
||||
Рис.15. Графическое изображение решенияв плоскости ( x, t) при нулевой начальной скорости.
Теперь перейдем к случаю, когда начальное смещение равно нулю, а начальная
скорость является произвольной функцией координаты g (x). В этом случае решение имеет вид (15).
Значение величины u в каждой точке (x0, t0) можно интерпретировать как интеграл от начальной скорости в пределахот x0 −at0 до x0 + at0 , т.е.
|
1 |
x |
+at |
|
|
|
u (x0 ,t0 ) = |
0 |
∫ |
0 |
g(ς) dς |
(23) |
|
2a x |
|
|||||
|
−at |
0 |
|
|
||
|
|
0 |
|
|
|
|
В качестве примера построим решение задачи Коши в координатахx,t с начальными условиями
u(x,0) = 0 |
|
|
|
|
|
|
1 в интервале x (−1, 1) |
. |
|
|
|
||
ut (x,0) = |
|
|
|
|
||
0 −во всех остальных точках |
|
|
|
|
||
Подставляя в формулу (23) в каждой из шести областей (см. Рис.15) свои значения |
||||||
функции g(ζ) и свои пределы интегрирования, получим |
|
|
|
|||
В областях1 и 5 |
g(ς) = 0 и следовательно u(x,0) = 0; в остальных областях g(ς) =1, |
|||||
при этом |
|
|
|
|
1+ x + at , |
|
в области 2 пределы интегрирования от – 1 до x + at и u(x,0) = |
||||||
|
|
|
1 |
|
2a |
|
в области 3 пределы интегрирования от + 1 до –1 и u(x,0) = |
|
, |
||||
2a |
||||||
|
|
|
|
|||
в области 4 пределы интегрирования от x −at до 1 и u(x,0) = 1− x + at , 2a
в области 6 пределы интегрирования от x −at до x + at и u(x,0) = t .
С физической точки зрения рассматриваемый процесс можно пояснить следующим образом. Пусть точка x лежит правее промежутка (– 1, 1). При t = 0 промежуток интегрирования ( x −at , x + at ) вырождается в точку x, а затем при увеличении t он
расширяется в обе стороны со скоростью a. При t < x −a a этот промежуток будет находиться вне промежутка ( – 1, 1) и функция g (x) в нем будет равна нулю, а значит и
u(x, t) = 0, т.е. точка x покоится. Начиная с момента времени t = x −a a промежуток ( x −at ,
x + at ) будет покрывать интервал (– 1, 1) , в котором в котором функция g (x) равна единицеи точка x начнетперемещаться по мере прохождения фронта волны через точкуx.
Наконец, при t > x +a a промежуток ( x −at , x + at ) будет целиком содержать интервал (– 1, 1) и интегрирование будет сводиться к интегрированию в этом интервале, т.е. при t > x +a a смещение токи x будет оставаться постоянным и равным 1/a. Момент времени
t = x +a a является моментом прохождения заднего фронта волны через точкуx.
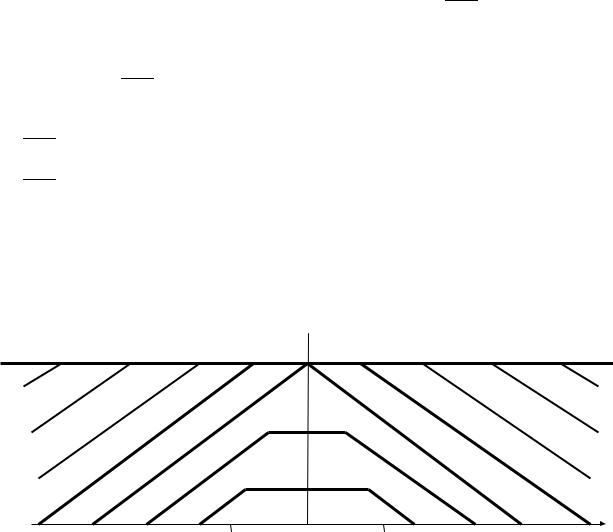
Этот процесс схематично проиллюстрирован на рис. 16. Таким образом, действие начального импульса приводит к тому, что с течением времени точки струны перемещаются на отрезок длиной u=1/a и остаются без движения в этом новом
положении. Иначе говоря, волна оставляет после себя след своего прохождения. В результате положения u=1/a сначала достигает точка с координатой x=0, после чего
область смещения постепенно распространяется на всю длинубесконечной струны.
u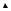
t = ∞
|
|
|
|
x |
|
–1 |
1 |
||||
|
|||||
Рис.16. Графическое изображение решенияв плоскости ( x, t) при нулевомначальномсмещении.
§ 5. Случай полубесконечной струны
Сформулируем задачу о движении полубесконечной струны, левый конец которой закреплен. В этом случае уравнение колебания струны следует записатьтолько для x > 0 :
|
u tt = a2u x x |
0 < x < ∞ |
(24) |
|
Начальные условия: |
u(x,0) = f (x) |
0 < x < ∞ |
(25) |
|
ut (x,0) = g(x) |
||||
|
|
|
||
Граничное условие: |
u (0,t) = 0 |
|
(26) |
Чтобы решить эту задачу вернемся частично к выводу формулы Даламбера (§ 2), записав решение уравнения (24) в виде
u (x,t) =ϕ (x −at) +ψ (x + at) , |
(27) |
|
1 |
|
1 |
|
x−at |
|
|
C |
|
|||
ϕ(x −at) = |
f (x −at) − |
|
∫ |
g(ς) dς − |
|
|||||||
2 |
2a |
2a |
||||||||||
где |
|
x |
|
|||||||||
|
|
|
|
|
0 |
|
(28) |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
1 |
|
x+at |
|
|
C |
|
||
ψ (x + at) = |
f (x + at) + |
|
∫ |
g(ς) dς + |
|
|||||||
2 |
|
2a |
|
2a |
||||||||
|
|
|
x |
|
|
|||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
В отличие от бесконечной струны начальные условия, т.е. функции f(x) и g(x) определены только для x >0 и решение может быть определено тоже только при x >0.
Это означает, что первая из формул (28) позволяет вычислить φ (x – a t) только при x– at > 0. В связи с этимпри x– at > 0 мы, каки раньше, можем записать
|
1 |
[ f (x −at) + f (x + at)]+ |
1 |
x+at |
|
u (x,t) = u (x,t) =ϕ (x −at) +ψ (x + at) = |
∫ g(ς) dς , |
||||
2 |
2a |
||||
|
|
x−at |
|||
|
|
|
|
a при x– at < 0 нам надо доопределить функцию φ (x – a t). Для этого воспользуемся граничным условием и подставим туда общее решение (27). В результате получим
ϕ (−ct) = −ψ (ct),
откуда
|
|
ϕ (x −at) = 1 |
|
|
|
1 |
|
at−x |
C |
|
|
|
f (at − x) − |
|
∫ g(ς) dς − |
||||||
|
|
2a |
2a |
|||||||
|
|
2 |
|
|
|
x |
||||
|
|
|
|
|
|
|
|
0 |
|
|
Подставив это выражение для φ в общее решение, мы окончательно получим |
||||||||||
|
1 |
[f (x −at) + f (x +at)]+ |
1 |
|
x+at |
|
|
|
|
|
|
2 |
|
|
∫ g(ς)dς |
при x ≥ at |
|
|
|||
|
|
|
||||||||
|
|
2a x−at |
|
|
|
|
|
|||
u (x,t) = |
1 |
|
1 |
|
x+at |
|
|
|
(29) |
|
|
[f (x −at) − f (at − x)]+ |
|
∫ g(ς)dς |
при x < at |
|
|
||||
2 |
2a |
|
|
|
||||||
|
|
|
at−x |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
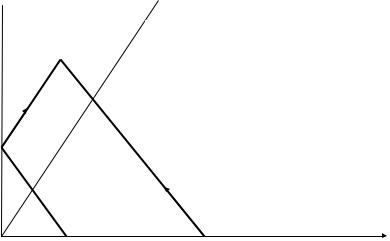
Таким образом, при x < at включается волна, отраженная от границы, что соответствует сменой знака на противоположный (см. Рис. 17).
t 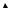
x= at
(x0, t0)
(at0 –x0, 0) |
(x0+at0, 0) |
x |
Рис. 17. Формирование отраженной волны |
|
|
§ 6. Метод разделения переменных для уравнения колебанийограниченной струны.
Рассмотрим задачу о колебаниях ограниченной струны длины l с нулевыми
граничными условиями первого рода и произвольными начальными условиями в отсутствии внешней силы. Такие колебания струны называются свободными. Решение
этой задачи сводится крешению волнового уравнения
при граничныхусловиях
и начальныхусловиях
u tt = a2u x x
u(0,t) = 0 u(l,t) = 0
u(x,0) = f (x) ut (x,0) = g(x)
(30)
(31)
(32)
при этом искомое решение должно быть нетривиальными ограниченным. В этом случае можно было бы решать задачупо формуле Даламбера
u (x,t) =ϕ (x −at) +ψ (x + at)
Однако определение функций ϕ (x −at) и ψ (x + at) по формулам, которые мы получили из начальныхусловий
|
1 |
|
1 |
|
x |
|
C |
|||
ψ (x) = |
f (x) + |
|
∫ g(ς) dς + |
|
||||||
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
2a x |
|
2a |
||||
|
|
|
|
|
|
0 |
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
x |
|
C |
|||
ϕ(x) = |
f (x) − |
|
∫ g(ς) dς − |
|
||||||
|
|
|
|
|
|
|
|
|||
|
2 |
|
2a x |
2a |
||||||
|
|
|
|
|
|
0 |
|
|
|
|
встречает здесь те же затруднения, что и в случае полубесконечной струны, поскольку
функции f(x) и g(x) определены только для x >0 и решение может быть определено тоже только при x >0.
В связи с этим приходится искать продолжение функций f(x) и g(x) вне промежутка
(0, l), используя для этого граничные условия. Этот путь приводит, как мы помним, к построению отраженных волн и формированию решения в виде суперпозиции прямой и
обратной волны. Поскольку струна закреплена с обоих концов, то прямая и обратная волны будут пересекаться многократно, что мешает наглядно представить этот процесс.
Ситуация упростилась бы, если бы можно было посмотреть как формируется
решение отдельно по координате и по времени. Этот подход можно реализовать с помощью методом разделения переменных, который является одним из наиболее
распространенных методов математической физики, в чем мы ещё не раз убедимся. В соответствии с этим методом решение уравнения в частных производных ищется в виде произведения функций, каждая из которых зависит только от одной переменной. В
частности для уравнения (30) решение ищется в виде
u(x,t) = X (x)T (t) |
(33) |
Подставив это выражение в уравнение (30), получим
X (x)T ''(t) = a2 X (x)T (t)
Разделим обе части на a2 X (x)T (t) , тогда уравнение приметвид
