Учебник по УМФ первая часть

В. П. Трегубов

УРАВНЕНИЯМАТЕМАТИЧЕСКОЙ ФИЗИКИ

Курс лекций.

Часть I.

Санкт-Петербург

2015

УДК 501 (517.946)

ОГЛАВЛЕНИЕ

Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

Предмет математической физики

Основные понятияи определения Классификация квазилинейныхуравнений второго порядка

Гл а в а I. Скалярные и векторные поля.Дифференциальные операторы

§1. Скалярные поля

§2. Векторные поля

§3. Оператор Гамильтона и дифференциальные операторывторого порядка

Гл а в а II. Одномерное волновое уравнение

§1. Уравнение малыхпоперечныхколебаний струны

§2. Случай ограниченной струны

§3. Решение задачи Коши

Формула Даламбера

Частные случаи Графическаяинтерпретация

§4. Метод характеристик

§5. Случай полубесконечной струны

§6. Метод разделения переменныхдля уравненияколебания ограниченной струны

Замечание о колебании музыкальныхструн

§7. Вынужденные колебанияструны, закрепленной на концах

§8. Продольные колебания однородного стержня

§9. Случай ненулевых граничныхусловий

§10. Телеграфное уравнение

§11. Общая схема метода разделенияпеременных для однородных гиперболических уравнений

§12. Задача Гурса

§13. Теорема единственности решения краевыхзадач для одномерного волнового уравнения

Гл а в а III. Двумерные и трехмерные задачи для волнового уравнения

§1. Волны в трехмерном пространстве

Сферически симметричная задача Формула Пуассона

Физическая картина распространения волн в трехмерном пространстве

§2. Двумерное волновое уравнение

§3. Теорема единственности для двумерного волнового уравнения

§4. Трехмерное неоднородное волновое уравнение

§5. Точечный источник

§6. Уравнения малыхпоперечныхколебаний мембраны

§7. Граничные условия.

§8. Решение задачи о колебанияхкруглой мембраны

Гл а в а IV. Некоторые общие вопросы теории дифференциальных уравнений

гиперболического типа

§1. Задача Коши. Характеристики.

§2. Слабый разрыв. Фронт волны

Гл а в а V. Уравнение теплопроводности и диффузии

§1 . Уравнение теплопроволности для однородного стержня

§2. Граничные условияи ихфизический смысл

§3. Применение метода разделения переменных

§4. Задача о распространении теплав изотропном твердом теле

§5. Уравнение диффузии

§6. Принцип максимального значения.

§7. Теорема единственности для неоднородного уравнения теплопроводности

Введение

Предмет математической физики.

Математическая физика это раздел высшей математики, в котором физические

процессы описываются дифференциальными уравнениями в частных производных, а также интегральными уравнениями.

Математическая физика формировалась в результате необходимости решать задачи физики, формулировка которых была невозможна без использования уравнений в частных производных, то есть уравнений, в которые входят неизвестная функция и её

частные производные.

Само обращение к частным производным было обусловлено тем, что величины, описывающие состояние объекта исследования и процессы в нём происходящие, как

правило, являются функциями нескольких переменных. (С другой стороны) В то же время, большинство физических законов было сформулировано для физических величин,

характеризующих тело в целом (масса, объём, площадь поверхности, температура, теплоёмкость и т.д.). Эти величины связывались между собой определёнными соотношениями и могли меняться во времени. Однако изменения физических величин

при переходе от одной точки тела к другой не рассматривались. Это видно, в частности, на примерах задач механики, в которых от понятий материальной точки и абсолютного тела необходимо было перейти к новому физическому понятию – деформируемые тела

и среды, которые включают в себя твёрдые деформируемые тела, жидкие и газообразные среды. По существу нужно было законы механики, сформулированные для

тела в целом, записать для каждой точки этого тела, используя функции, зависящие от пространственных координат каждой точки и времени. Примером могут служить

уравнения движения идеальной сжимаемой жидкости, впервые представленные Л. Эйлером в 1755 г.

Аналогичная ситуация сложилась, когда нужно было получить уравнения для

описания процессов теплопроводности и распределения тепла, в которых нужно было прейти от понятия температура тела к понятию температуры в каждой точке тела. Со

временем перечень таких явлений расширялся. Появились уравнения в частных производных для описания процессов в электростатическом поле, процессов диффузии и т.д.

Однако некоторые физические законы, такие как законы электромагнитного поля, впервые опубликованные Максвеллом в 1873 г. в его «Трактате об электричестве и магнетизме, с самого начала формулировались на языке уравнений в частных

производных, точнее говоря, систем таких уравнений.

В целом, те или иные уравнения в частных производных нужно рассматривать как

математические модели физических процессов или состояний среды (в стационарном случае), в которых величины, характеризующие этот процесс или состояние, являются функциями нескольких переменных. При этом следует иметь в виду, что каждое

уравнение получено при определенных допущениях и предположениях, которые позволяют идеализировать некоторые свойства объекта или процесса и пренебречь

другими. Строго говоря, уравнения колебания струны, стержня, мембраны, надо бы называть уравнения колебания модели струны, модели стержня и модели мембраны, и хотя слово модель каждый раз не упоминается, оно, тем не менее, каждый раз

подразумевается.

Следует также отметить, что для некоторых уравнений в частных производных оказывалось целесообразным свести их к интегральным уравнениям, то есть к

уравнениям, в которыхнеизвестная функция входит под знакинтеграла.

Со временем оказалось, что к уравнениям с частными производными приходится обращаться не только при записи физических законов, но и законов, сформулированных

для других областей знания:экономики, социологии, физиологии и т.д. При этом методы решения уравнений с частными производными не зависели от природы описываемого

процесса или состояния. Это привело к формированию раздела математики под названием

теория дифференциальных уравнений в частных производных, а математическая физика стала разделом высшей математики. Однако смешивать эти два понятия не следует, тем

более что в математической физике, как уже отмечалось, используются и интегральные уравнения, методы решения которых составляют раздел высшей математики под названием теория интегральных уравнений. Далее мы будем иметь дело толь с

уравнениями математической физики, дифференциальными или интегральными. Предлагаемый учебник частично возвращает читателя к первоосновам

математической физики, имея в видунеобходимость подготовить специалистов, умеющих не только знать, как выводить и решать известные уравнения, но и осуществлять математическую постановку новых физических задач, что особенно важно для студентов

направления «Прикладные математика и физика».

С этой целью в предлагаемом курсе лекций особое внимание уделяется физической

основе уравнений в частных производных, которые можно рассматривать как средство математического моделирования физических процессов, а также физическому смыслу начальныхи граничныхусловий. Такие разделы математической физики как специальные

функции, теория интегральных уравнений и некоторые численные методы решения уравнений математической физики отнесены к дополнительным главам к основному

курсуи напечатаны отдельно.

Основные понятия и определения.

Для уравнений математической физики независимыми переменными обычно

являются координаты x, y, z (или другие пространственные координаты) и время t. Именно для этихнезависимыхпеременныхмы и сформулируем основные определения.

Уравнение, связывающее независимые переменные x, y, z и t, неизвестную функцию

u (x, y, z, t) и частные производные от неизвестной функции, называется

дифференциальным уравнением в частных производных.

Оно имеет вид

старшие производные входят в уравнение только в первой степени, а коэффициенты при этихпроизводныхявляются функциями только независимыхпеременных.

Если же указанные коэффициенты зависят также и от неизвестной функции и её производныхболее низкого порядка, то такое уравнение называется квазилинейным.

Уравнение называется линейным, если оно линейно относительно неизвестной

функции и всех его производных, а коэффициенты являются функциями только независимых переменных. В качестве примера приведем вид линейного уравнения

второго порядка относительно двухнезависимыхпеременныхx и y,

где коэффициенты a11, a12, a22, b1, b2, c зависят только от x и y. В качестве одной из

переменной может выступать время t.

Если функция независимых переменных в правой части уравнения равна нулю, то

уравнение называется однородным.

Решением уравнения в частных производных называется всякая функция u(x, y, z, t),

которая, будучи подставлена вместе со своими частными производными в уравнение,

обращает его в тождество.

Каждое уравнение в частныхпроизводныхимеет бесчисленное множество решений.

При решении конкретной физической задачи выбирают то решение, которое вытекает из её физического смысла. Одним из видов таких условий являются начальные условия, относящиеся к моменту времени, с которого начинается изучение данного физического

процесса. Для уравнения, содержащего производные по времени порядка n, нужно в начальный момент времени задать саму функцию и её производные до порядка n – 1

включительно, которые будут являться функциями только координат. Если физическая задача формулируется для некоторой ограниченной области, то на границе формулируются граничные условия. Для этого сама функция и (или) её производные (не

выше n – 1 порядка, где n – порядок старшей производной по координате) задаются как функции времени.

Путем линейного преобразования независимых переменных уравнение в частных производных можно привести к наиболее простому виду. Так уравнение (2) можно привести к виду, не содержащему смешанного произведения. Наиболее простой вид то го или иного уравнения называется каноническим видом этого уравнения. Этот вид может оказаться не единственным.

Классификация квазилинейных уравнений второго порядка

Формулировка большинства традиционных задач физики приводит к линейным уравнениям в частныхпроизводныхвторого порядка с постоянными коэффициентами.

Уравнение (7) в точке М0 принадлежит к гиперболическому типу, если в этой точке квадратичная форма (8) при приведении её к сумме квадратов имеет все коэффициенты, кроме одного, одного, определенного знака, а оставшийся один коэффициент

противоположного знака.

Уравнение (7) в точке М0 принадлежит к параболичекому типу, если в этой точке

квадратичная форма (8) при приведении её к сумме квадратов имеет только один коэффициент, равный нулю, а все другие коэффициенты имеют одинаковые знаки.

Поскольку коэффициенты aij, и bi являются функциями x1,…xn, то при переходе от

одной точки к другой уравнение (7) может менять свою принадлежность к тому или иному типу. В связи с этим, уравнение принадлежит к тому или иному типу в некоторой

области D, если оно принадлежит кэтомутипув каждой точке этой области.

Для квазилинейного уравнения второго порядка с двумя независимыми переменными тип уравнения определяется более наглядно. Для этого его нужно записать

в следующем виде:

в) кэллиптическомутипу, если B2 − AC < 0.

В записанных выше уравнениях (3) – (6) коэффициенты при производных являются постоянными, поэтому при переходе от одной точки к другой тип уравнения сохраняется.

В связи с этим во всей области решения задачи уравнение (3) является уравнением гиперболического типа, уравнение (4) – уравнением параболического типа, а уравнения

(5) и (6) уравнениями элептического типа.

Г л а в а I. Скалярные и векторные поля. Дифференциальные операторы

§ 1. Скалярные поля

Цель этой короткой главы – лишь напомнить некоторые понятия, результаты, их

математические формулировки и физический смысл, которые излагаются в курсе математического анализа, и которые потребуются нам в дальнейшем при изложении

материала. Это касается понятий скалярного и векторного полей, а также дифференциальныхоператоров, применяемых кэтим полям.

Наряду с понятием скалярной и векторной физической величины в математической

физике часто пользуются понятиями скалярного поля и векторного поля.

Если в каждой точке М области D задано значение скалярной величины u, то эта u = u (M ). В этом случае говорят, что

в области D задано скалярное поле.

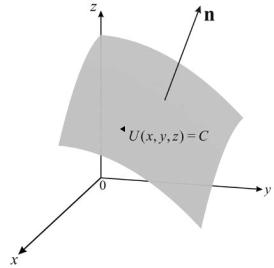
Для скалярного поля вводится понятие поверхности уровня, которая определяется как геометрическое место точек, в которых функция u имеет постоянное значение. В

трехмерном случае это можно записать как

u (x, y, z) = C .

Градиент скалярной величины

Наряду с понятием поверхности уровня вводится понятие градиента, т.е. векторной величины, направление которой совпадает с направлением нормали кповерхности уровня скалярного поля (Рис. 1). Проекциями этого вектора на координатные оси служат частные

производные от функцииu (x, y, z), т. е. :

Рис. 1. К понятию градиента скалярной функции

Таким образом, градиент это вектор, который представляет собой результат применениянекоего дифференциального оператора кскалярной функции.

Если векторное поле А в каждой точке М может быть задано какградиент некоторой функции U, т. е. А= grad U, то такое поле называют потенциальным, а функцию U –

потенциалом.

Физический смысл градиента заключается в том, что его направление совпадает с направлением наибольшего возрастания скалярной величины. Так градиент температуры

направлен к источнику тепла, а градиент потенциала электростатического поля к одиночномузаряду и т.д. Модуль градиента характеризует степень возрастания скалярной величины.

гравитационное поле, электромагнитное поле, поле скоростей текущей жидкости и т.д. Для векторного поля вводят понятие векторной линии, т.е. линии, направление

касательной к которой в каждой точке совпадает с направлением вектора А(М) (Рис. 2). Если векторное поле определяется функцией

то векторная линия в пространстве задается следующей системой дифференциальныхуравнений

Рис.2.К понятиювекторной линии

Поток вектора

Важным понятием для векторного поля является поток вектора. Если векторное поле задано выражением (2), то для всякой поверхности S с нормалью n можно записать интеграл по этой поверхности от проекции вектора A на нормаль n, а именно

где α, β, γ – направляющие косинусы нормали. Формула (4) и определяет поток вектора A через поверхность S.

Физический смысл потока нагляднее всего иллюстрируется на примере потока жидкости, который есть не что иное, как объём жидкости, пересекающий единицу поверхности в единицу времени. Тогда поток жидкости через площадку dS будет равен

объему параллелепипеда с ребром, равным скорости потока V и высотой, равной Vn (см. Рис. 3), а потокжидкости через всю поверхность S будет соответственно равен

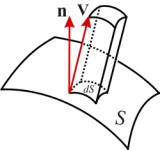
Рис. 3. К физическомусмыслупотока вектора

Дивергенция вектора

Понятие потока вектора лежит в основе другого важного понятия – дивергенции вектора. Для его определения нужно рассмотреть некоторую точкувекторного поля А(M) и окружить её замкнутой поверхностью S, целиком содержащейся в поле. В поле скоростей жидкости это будет соответствовать алгебраической сумме втекающей и

вытекающей жидкости, которая будет равна нулю, если внутри объема отсутствуют источники и стоки жидкости.

Теперь возьмем отношение потока вектора А кобъемуV внутри поверхности S

∫∫An dσ

и найдем предел этого отношения при V, стремящемся к нулю. Этот предел и называется

дивергенцией или расходимостью вектора А в точке М, а именно

∫∫An dσ

Дифференциальная форма дивергенции векторного поля, заданного формулой (2), имеет вид:

Таким образом, результат применения оператора дивергенции к вектору является величиной скалярной.

Пользуясь выражением для дивергенции (7), теорему Остроградского можно записать в векторном виде

Эта форма теоремы Остроградского для поля текущей жидкости выражает тот

очевидный факт, что потокжидкости через поверхность равен суммарной мощности всех источников и стоков, т.е. количеству жидкости, возникающей в рассматриваемой области в единицувремени.