
- •1.3. Полнота, непротиворечивость, разрешимость исчисления высказываний
- •Семантика и синтаксис
- •Интерпретации ив
- •Независимость правил вывода
- •1.4. Исчисление высказываний гильбертовского типа
- •Схемы аксиом гильбертовского ив
- •Правило вывода
- •Секвенции, квазивывод
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
Правило вывода
![]()
Это
правило называется modus
ponens
(кратко: MP).
Оно позволяет заявить о выводимости
формулы
![]() если ранее были выведены
если ранее были выведены![]() и
и![]()
Последовательность
формул
![]() называетсявыводом,
если каждое
называетсявыводом,
если каждое
![]() – либо аксиома, либо получается из
каких-либо двух формул из
– либо аксиома, либо получается из
каких-либо двух формул из![]() применением правила вывода. Формула
применением правила вывода. Формула![]() называетсявыводимой
(или доказуемой),
если существует вывод
называетсявыводимой
(или доказуемой),
если существует вывод
![]() где
где![]() Доказуемые формулы называются такжетеоремами.
Приведём примеры выводов. Как обычно,
внешние скобки в формулах мы будем часто
опускать.
Доказуемые формулы называются такжетеоремами.
Приведём примеры выводов. Как обычно,
внешние скобки в формулах мы будем часто
опускать.
Пример
1. Вывод
формулы
![]()
(аксиома
2 при
![]()
![]()
![]()
 (аксиома
1);
(аксиома
1); (из
(1) и (2) по modus ponens);
(из
(1) и (2) по modus ponens);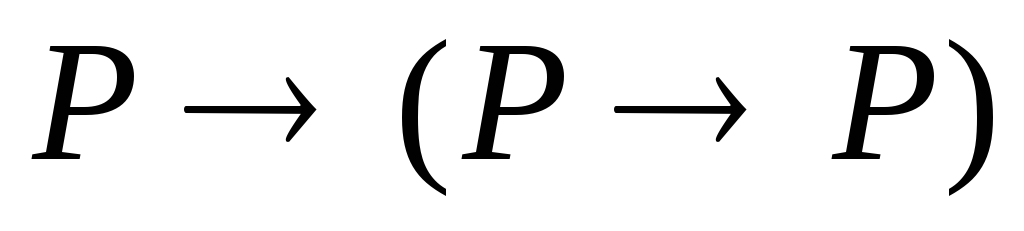 (аксиома
1);
(аксиома
1); (из
(3) и (4) по modus ponens).
(из
(3) и (4) по modus ponens).
Пример
2. Вывод
формулы
![]()
(1)-(5)
— вывод формулы
![]() (см. пример 1);
(см. пример 1);
 (аксиома
8);
(аксиома
8); (из
(5) и (6) по MP);
(из
(5) и (6) по MP);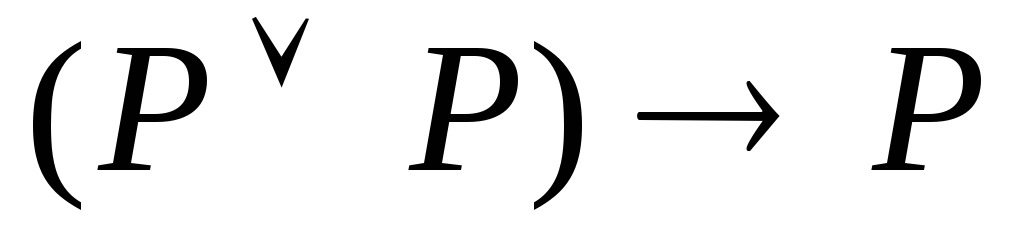 (из
(5) и (7) по MP).
(из
(5) и (7) по MP).
Секвенции, квазивывод
Пусть
![]() – совокупность формул ИВ (возможно,
пустая). Последовательность формул
– совокупность формул ИВ (возможно,
пустая). Последовательность формул![]() где
где![]() называетсяквазивыводом
(формулы
называетсяквазивыводом
(формулы
![]() если каждое
если каждое![]() – либо аксиома, либо формула из
– либо аксиома, либо формула из![]() либо получается из предшествующих
формул по правилу modus ponens. Если для
формулы
либо получается из предшествующих
формул по правилу modus ponens. Если для
формулы![]() существует квазивывод из формул
существует квазивывод из формул![]() то мы говорим, что формула
то мы говорим, что формула![]() выводится из
выводится из![]() и пишем
и пишем![]() Запись
Запись![]() естественно назвать секвенцией.
естественно назвать секвенцией.
Квазивывод
можно интерпретировать так: мы добавляем
к списку аксиом формулы некоторой
совокупности
![]() и осуществляем вывод нашей формулы из“расширенного”
списка аксиом.
и осуществляем вывод нашей формулы из“расширенного”
списка аксиом.
Лемма
о дедукции.
Пусть
![]() – совокупность формул, а
– совокупность формул, а![]() и
и![]() – формулы. Тогда
– формулы. Тогда![]() в том и только том случае, если
в том и только том случае, если![]()
Доказательство.
Необходимость.
Пусть существует квазивывод формулы
![]() из формул совокупности
из формул совокупности![]()
![]() Здесь каждое
Здесь каждое![]() – либо аксиома, либо формула из
– либо аксиома, либо формула из![]() либо получается из предшествующих
формул по MP. Нам надо получить квазивывод
формулы
либо получается из предшествующих
формул по MP. Нам надо получить квазивывод
формулы![]() из
из![]() Значит, можно использовать формулу
Значит, можно использовать формулу![]() Продолжим приведённый ранее квазивывод:
Продолжим приведённый ранее квазивывод:![]() Это будет квазивывод формулы
Это будет квазивывод формулы![]() из
из![]() действительно,
действительно,![]() а
а![]() получается из
получается из![]() и
и![]() по MP.
по MP.
Достаточность.
Пусть есть квазивывод
![]() где
где![]() а каждое
а каждое![]() удовлетворяет одному из условий:
удовлетворяет одному из условий:
(а)
![]() – аксиома;
– аксиома;
(б)
![]()
(в)
![]()
(г)
![]() получается из предыдущих по MP.
получается из предыдущих по MP.
Рассмотрим последовательность формул
![]()
![]() .
. . ,
.
. . ,
![]()
![]()
Последняя
формула совпадает с формулой
![]() для которой надо написать квазивывод.
Но последовательность
для которой надо написать квазивывод.
Но последовательность![]() в общем случае не является квазивыводом.
Мы её будем“исправлять”,
двигаясь слева направо и вставляя перед
формулой
в общем случае не является квазивыводом.
Мы её будем“исправлять”,
двигаясь слева направо и вставляя перед
формулой
![]() ряд формул так, чтобы получился квазивывод.
ряд формул так, чтобы получился квазивывод.
Предположим,
что формулы
![]() . . . ,
. . . ,![]() уже просмотрены и недостающие до
квазивывода формулы вставлены. Рассмотрим
формулу
уже просмотрены и недостающие до
квазивывода формулы вставлены. Рассмотрим
формулу![]()
Случай
(а):
![]() – аксиома. Тогда
– аксиома. Тогда![]() заменяем последовательностью
заменяем последовательностью![]()
![]()
![]() в которой первая и вторая формулы –
аксиомы, а третья получена из них поmodus
ponens.
в которой первая и вторая формулы –
аксиомы, а третья получена из них поmodus
ponens.
Случай
(б):
![]() – формула из
– формула из![]() В этом случае делаем то же самое:
В этом случае делаем то же самое:![]()
![]()
![]() Теперь первая формула – не аксиома, а
элемент из
Теперь первая формула – не аксиома, а
элемент из![]() что допустимо.
что допустимо.
Случай
(в):
![]() В этом случае скобка
В этом случае скобка![]() имеет вид
имеет вид![]() Вставляем перед ней 4 формулы, которые
вместе с
Вставляем перед ней 4 формулы, которые
вместе с![]() составляют вывод формулы
составляют вывод формулы![]() (см. пример 1).
(см. пример 1).
Случай
(г):
![]() получается из предыдущих по правилу
вывода. В этом случае среди формул
получается из предыдущих по правилу
вывода. В этом случае среди формул![]() есть формулы
есть формулы![]() и
и![]() Очевидно,
Очевидно,![]() при некотором
при некотором![]() Значит, в последовательности
Значит, в последовательности![]() уже встречались формулы
уже встречались формулы![]() и
и![]() Формулу
Формулу![]() заменяем последовательностью формул
заменяем последовательностью формул
![]() (аксиома);
(аксиома);
![]() (получается
по MP);
(получается
по MP);
![]() (получается
по MP).
(получается
по MP).
Применим лемму о дедукции к доказательству выводимости формул.
Пример 3. Доказать выводимость формулы
![]()
Решение. По лемме о дедукции
![]() выводима
выводима
![]()
![]()
![]()
![]()
![]()
![]()
Последняя
секвенция имеет квазивывод
![]() (двукратное применениеMP).
(двукратное применениеMP).
Пример
4. Чтобы
осуществить связь между генценовским
и гильбертовским исчислениями
высказываний, докажем правило вывода
№ 1:
![]()
Решение.
По условию есть квазивывод
![]() и квазивывод
и квазивывод![]() где каждое
где каждое![]() или
или![]() – либо аксиома, либо элемент из
– либо аксиома, либо элемент из![]() либо получается поMP.
Добавим
аксиому
либо получается поMP.
Добавим
аксиому
![]() и получим квазивывод
и получим квазивывод![]()
![]()
![]()
![]()
![]()
Пример
5. Докажем
правило
![]() Это правило называется“разбор
случаев”
(здесь
Это правило называется“разбор
случаев”
(здесь
![]() – первый случай,
– первый случай,![]() – второй).
– второй).
Решение.
По лемме о дедукции мы можем считать,
что существует квазивывод
![]() и квазивывод
и квазивывод![]() Объединим их:
Объединим их:
![]()
Продолжим
эту последовательность до квазивывода
![]()
Добавим
аксиому
![]()
Применим
modus
ponens:
![]()
Ещё
раз modus
ponens:
![]()
Добавим
формулу
![]()
Применим
modus
ponens, получим
![]()
Таким
образом у нас получился квазивывод
формулы
![]() из
из![]() и
и![]()
Пример
6. Докажем
правило
![]()
Решение.
Напишем квазивывод формул
![]() и
и![]() из
из![]()
![]() Затем
добавим три формулы:
Затем
добавим три формулы:
![]() (аксиома),
(аксиома),![]() (из двух последних по MP),
(из двух последних по MP),![]() (из последнего и четвёртого от конца по
MP).
(из последнего и четвёртого от конца по
MP).
Пример
7. Докажем
правило
![]()
Решение.
По лемме о дедукции имеем:
![]() и
и![]() Напишем аксиому (10):
Напишем аксиому (10):![]() Так как из
Так как из![]() выводимо
выводимо![]() то поmodus
ponens будет
то поmodus
ponens будет
![]() По условию
По условию![]() Снова применяяmodus
ponens, получим:
Снова применяяmodus
ponens, получим:
![]()
Приведём несколько формул, доказательство которых не использует закон исключённого третьего, т.е. аксиому (11).
(а)
![]()
Доказательство. По лемме о дедукции достаточно доказать, что
![]()
Для этого, в свою очередь, достаточно доказать, что
![]()
![]() и
и
![]()
![]()
Так
как
![]() и
и![]() доказываются аналогично, то будем
доказывать только
доказываются аналогично, то будем
доказывать только![]() По лемме о дедукции
По лемме о дедукции![]() равносильно следующему:
равносильно следующему:![]() Добавив к этой последовательности
аксиому (6), получим квазивывод формулы
Добавив к этой последовательности
аксиому (6), получим квазивывод формулы![]() из
из![]() и
и![]()
![]()
(b)
![]()
Доказательство.
Из аксиом
![]() и
и![]() по принципу разбора случаев при
по принципу разбора случаев при![]() получим:
получим:
![]()
![]()
Так
как
![]() и
и![]() то
то![]() Аналогично
Аналогично![]() По принципу разбора случаев (при
По принципу разбора случаев (при![]() получим:
получим:
![]()
![]()
Из
![]() и
и![]() получаем:
получаем:![]() Отсюда по лемме о дедукции получим(b).
Отсюда по лемме о дедукции получим(b).
(c)
![]() (закон
контрапозиции).
(закон
контрапозиции).
Доказательство.
По лемме о дедукции (применённой дважды)
получим, что доказательство утверждения
(с) сводится к доказательству утверждения
![]() Так как
Так как![]() и
и![]() то по правилу из примера 7 получаем:
то по правилу из примера 7 получаем:![]()
(d)
![]()
Доказательство.
Очевидно,
![]() и
и
![]() Отсюда по правилу из примера 7 получаем
Отсюда по правилу из примера 7 получаем![]() а значит, по лемме о дедукции будем иметь
а значит, по лемме о дедукции будем иметь![]()
Оказывается,
формулы, обратные к формулам (с) и (d),
невозможно
доказать без использования закона
исключённого третьего, т.е. формулы
![]() и
и![]() невыводимы в ИИВ (интуиционистском
исчислении высказываний). Докажем эти
формулы в классическом ИВ, т.е. пользуясь
аксиомой (11).
невыводимы в ИИВ (интуиционистском
исчислении высказываний). Докажем эти
формулы в классическом ИВ, т.е. пользуясь
аксиомой (11).
(е)
![]()
Доказательство.
По лемме о дедукции достаточно доказать,
что
![]() Так как
Так как![]() – аксиома, то нам теперь достаточно
получить
– аксиома, то нам теперь достаточно
получить![]() По принципу разбора случаев для этого
достаточно доказать
По принципу разбора случаев для этого
достаточно доказать![]() и
и![]() Первое соотношение очевидно, а второе
доказывается так: из
Первое соотношение очевидно, а второе
доказывается так: из![]() и
и![]() по правилуmodus
ponens получаем
по правилуmodus
ponens получаем
![]() а, имея
а, имея![]() и
и![]() по правилу из примера 6 получаем
по правилу из примера 6 получаем![]()
(f)
![]()
Доказательство.
Так как мы можем использовать аксиому
(11), нам достаточно доказать, что
![]() По принципу разбора случаев достаточно
доказать, что
По принципу разбора случаев достаточно
доказать, что![]() и
и![]() Первое соотношение очевидно, а второе
следует из правила, полученного в примере
6.
Первое соотношение очевидно, а второе
следует из правила, полученного в примере
6.
Следующая
теорема показывает, что в списке аксиом
классического исчисления высказываний
аксиома (10) (![]() )
является лишней, так как следует из
остальных аксиом. В этой теореме
существенно, что мы можем пользоваться
аксиомой (11) – законом исключённого
третьего. В интуиционистской логике
аксиома (10) лишней не является.
)
является лишней, так как следует из
остальных аксиом. В этой теореме
существенно, что мы можем пользоваться
аксиомой (11) – законом исключённого
третьего. В интуиционистской логике
аксиома (10) лишней не является.
Теорема. Аксиома (10) следует из аксиом (1)-(9), (11).
Доказательство.
По лемме о дедукции достаточно доказать,
что
![]() Так как
Так как![]() – аксиома, то утверждение сводится к
доказательству секвенции
– аксиома, то утверждение сводится к
доказательству секвенции![]() По принципу разбора случаев достаточно
установить, что
По принципу разбора случаев достаточно
установить, что
![]()
![]()
и
![]()
![]()
По
правилу МР имеем:
![]() и
и![]() Напишем аксиому (9):
Напишем аксиому (9):![]() Тогда последовательность
Тогда последовательность
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
будет
квазивыводом формулы
![]() из
из![]()
![]()
![]() что доказывает секвенцию
что доказывает секвенцию![]() Секвенция
Секвенция![]() очевидна.
очевидна.
