Family solution to odes

The last numerical method of solving chemical ODEs discussed is the family method

(e.g., Crutzen 1971; Turco and Whitten 1974; Austin 1991; Elliott et al. 1993;

Jacobson 1994). This method is less accurate than Gear’s method for the same

time step and must be tuned for each application. It is fast and useful for several

applications.

The theory behind the family method is that some groups of gases, or families,

exist in which atoms transfer quickly among species in the family but are lost only

slowly from the family. Example families are the odd oxygen, odd hydrogen, odd

nitrogen, and odd chlorine families. Some of the major species in these families are

Odd oxygen: [OT] = [O] + [O(1D)] + [O3] + [NO2] (12.92)

Odd hydrogen: [HOT] = [OH] + [HO2] + [H2O2] (12.93)

Odd nitrogen: [NOT] = [NO] + [NO2] + [NO3] (12.94)

Odd chlorine [ClT] = [Cl] + [ClO] + [ClO2] (12.95)

For example, oxygen atoms in the odd-oxygen family cycle among the species

atomic oxygen, excited atomic oxygen, and ozone by the reactions,

Cycling of oxygen atoms among these reactions is fast, whereas loss of oxygen

atoms out of this group of reactions is slower.

The family solution to ODEs for a time step requires four steps. First, rates of

production and loss of individual species are calculated from initial concentrations.

These rates are then summed across a family. The family concentration is then

advanced with a forward Euler approximation applied to the summed production

and loss terms. Finally, species concentrations are repartitioned in the family for

the next time step.

Suppose a system contains four species (A, B, C, and D) and two families,

[Fam1] = [A] + [B] + [C] [Fam2] = [D] (12.97)

If the reactions

A →B (ka) B→C (kb) C→D (kc) (12.98)

occur in the system, the first step in the family solution method is to calculate rates

of production and loss of the individual species, A, B, C, and D:

The second step is to sum rates of production and loss across each family. Taking

the time derivative of (12.97) and substituting (12.99) into the result gives

The third step is to advance the family concentration over a time step with a forward

Euler. For example,

Substituting (12.100) into (12.101) gives

Fourth, species concentrations must be extracted from family concentrations. One

method of extracting species concentrations is to calculate and apply partitioning

ratios. Such ratios are calculated by summing the concentrations of the species in

the family as

Individual species concentrations are then found from the family concentrations with

In these equations, the partitioning ratios [B]t/[A]t and [C]t/[A]t are currently

unknown. In the case of species D, its final concentration is that of the family it

resides in, since no other species is in the family. Thus, [D]t = [Fam2]t = hkc[C]t−h.

The simplest but least accurate way to estimate partitioning ratios is to assume

that each species in the family is in steady state. With this method, the individual

rates of reaction of species B and C are set to zero:

The partitioning ratios of B and C are then estimated as

respectively. Substituting (12.106) into (12.104) gives the final species concentrations

of A, B, and C, respectively, as

A second way to estimate partitioning ratios is to linearize the ODEs of the

individual species as

and then to integrate each equation. The results are

[

These estimates are substituted into the right sides of (12.104).

A third way to estimate partitioning ratios is to finite-difference the ODEs as

and then to rearrange the equations into a matrix equation as

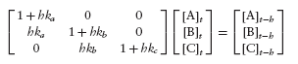
Solving the matrix equation for [A]t, [B]t, and [C]t then substituting the results into

the right sides of (12.104) gives final partitioned concentrations.

In the example above, the reactions were unimolecular. Most chemical reactions

are bimolecular. When bimolecular reactions are used, the first derivatives need to

be linearized for use in (12.111). If the bimolecular reaction A + C → B + D (kac)

is added to (12.98), the linearized finite-difference forms for A, B, and C are

respectively. The resulting matrix is (Jacobson 1994)

Solving this matrix equation gives concentrations that can be used to estimate

partitioning ratios.

The advantages of the family method are that it is fast, since it can use a long

time step, and it may be accurate for moderate- to low-stiffness systems. The disadvantages

are that the families need to be designed carefully and validated for each

set of chemistry, and the accuracy of the method decreases with increasing stiffness.

Also, although families are generally long-lived, the forward Euler solution for the

family often results in negative concentrations. In such cases, the time step must be

reduced and the family concentration must be recalculated. This reduces the speed

advantage of the family method.