metodyOKS(1)

Министерство образования и науки Российской Федерации

ФГБОУ ВПО

Российский государственный гидрометеорологический университет

(РГГМУ)

Кафедра прикладной экологии

Лабораторная работа 1

Предварительный анализ исходных данных

р. Тура - г. Тюмень 1931-1970

Выполнил: ст. гр. Э-386

Свердлова О.А

Проверила:

Урусова Е.С.

Санкт-Петербург 2014

Цели работы:

Выявить основные особенности исходных рядов наблюдения

Задачи работы:

1. Провести визуальную оценку исходных рядов наблюдения;

2. Рассчитать функцию распределения и обеспеченности;

3. Оценить основные числовые характеристики рядов наблюдения.

Исходными данными к работе являются ряды наблюдений за среднегодовым и максимальным расходом воды реки Тура - г. Тюмень 1931-1970.

Теоретические сведения

Множество, включающее в себя все однородные объекты (например, все данные об уровнях за период существования водного объекта…), которым присущи или не присущи определенные количественные или качественные признаки, образует генеральную совокупность. Основное отличие генеральной совокупности заключается в том, что все числовые характеристики и закон распределения случайной величины Х могут быть установлены по этой совокупности значений с точностью, равной точности определения исходных данных.

Ряд наблюдений за короткий период в n лет, взятый из генеральной совокупности, называется выборочной совокупностью или выборкой, а сами наблюдения, вошедшие в этот ряд, выборочным.

Одной из основных задач статистического анализа является получение по имеющейся выборке достоверных сведений об интересующих исследователя характеристиках генеральной совокупности. Поэтому важным требованием к выборке является ее репрезентативность, то есть правильная представимость в ней пропорций генеральной совокупности. Достижению репрезентативности может способствовать такая организация эксперимента, при которой элементы выборки извлекаются из генеральной совокупности случайным образом. Репрезентативность не всегда зависит от объема выборки.

Случайной величиной называется величина, которая в результате испытания может принимать различные значения в зависимости от случайного исхода испытания. Различают два типа случайных величин: непрерывные и дискретные.

Непрерывная случайная величина может принимать любые численные значения в некотором диапазоне, который, в частности, может быть и бесконечным. Примером непрерывной случайной величины в данной работе служат характеристики стока; средний годовой, максимальный.

Дискретная случайная величина может принимать только конечное или счетное множество значений.

Функцией распределения случайной величины Х (1) называется функция вида

F(x) =p(X<x), (1)

где х – заданное значение случайной величины, Х – возможные ее значения.

Функция распределения показывает вероятность получения в результате испытания значения случайной величины Х меньше, чем заданное значение х. В гидрологических расчетах обычно вместо нее используется функция обеспеченности(2):

P (х. )=1-F(x)=p(X≥x), (2)

которая показывает вероятность получить в испытании значение Х, большее или равное заданному значению х.

Числовые характеристики

Характеристики, назначение которых - выразить в сжатой форме наиболее существенные особенности распределения называются, числовыми характеристиками или параметрами распределения случайной величины.

Числовые характеристики, используемые в качестве расчетов, разделяют на характеристики положения, показывающие расположение определенных характеристик распределения на числовой оси, и характеристики рассеивания.

Числовые характеристики положения показывают расположение определенных характеристик распределения на оси абсцисс. Среди них важнейшую роль играют математическое ожидание случайной величины (m_x), мода (М), медиана (Ме).

Математическое ожидание (центр распределения) определяется по последовательности значений случайной величины Х(3):

M_x=∑x_i / N, (3)

где N-объем генеральной совокупности.

Мода дискретной случайной величины - это ее наиболее вероятное значение. Определение моды в этом случае производится по многоугольнику распределения как значение, имеющее наибольшую вероятность. Мода непрерывной случайной величины определяется по кривой распределения как значение Х, обладающее наибольшей плотностью распределения.

Медиана - это значение случайной величины, для которого(4)

р (Х<Ме)=р(Х>Ме), (4)

т.е. вероятность значений Х, больших или меньших Ме, одинакова. Медиана определяется с помощью функции распределения или обеспеченности как значение Х, имеющее обеспеченность, равную 50 %.

Другим классом числовых характеристик являются характеристики рассеивания. Они характеризуют степень и форму рассеивания возможных значений Х относительно математического ожидания. Среди них важную роль играют: дисперсия, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии.

Дисперсией D_x (5) случайной величины Х называется математическое ожидание квадрата соответствующей центрированной величины

D_x=∑(x_i-m_x)²/ N. (5)

Для характеристики рассеивания часто удобнее пользоваться величиной, размерность, которой совпадает с размерностью случайной величины. Это дает возможность сопоставить рассеивание со значениями самих величин Х. В качестве такой величины может служить корень квадратный из дисперсии. Эта величина называется средним квадратическим отклонением или стандартом и обозначается через σ_х (6):

Σ_х=√D_x. (6)

Для описания заведомо положительных величин большое распространение получила безразмерная характеристика рассеивания – коэффициент вариации(7):

С_v= σ_х/m_x. (7)

Коэффициент вариации не зависит от среднего и может быть использован для сопоставления изменчивости различных процессов.

Для характеристики симметричности рассеивания значений случайной величины относительно математического ожидания применяется безразмерная величина - коэффициент асимметрии(8):

С_s=∑(х_i-m_x)/N/ σ_х. (8)

Асимметрия может быть положительной и отрицательной. Знак асимметрии зависит от соотношения числовых характеристик положения: моды и математического ожидания. Если m_x>M, то С_s<0-положительная симметрия. Если m_x<M-отрицательная симметрия.

Результаты работы

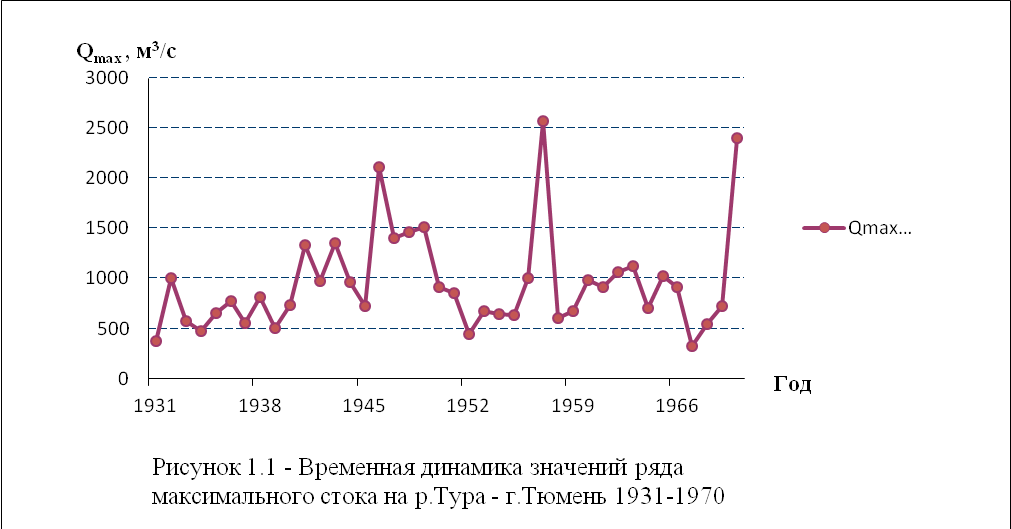
Таблица 1 - Исходные ряды значений среднегодового и максимального стока р. Тура - г.Тюмень 1931-1970
	№	Год	Qср, м3/с	Qmax ,м3/с
	1	1931	107	373
	2	1932	237	1000
	3	1933	103	576
	4	1934	61,3	472
	5	1935	151	654
	6	1936	105	774
	7	1937	147	551
	8	1938	112	812
	9	1939	79,3	508
	10	1940	132	732
	11	1941	196	1330
	12	1942	220	975
	13	1943	291	1350
	14	1944	182	961
	15	1945	148	719
	16	1946	286	2110
	17	1947	417	1400
	18	1948	300	1460
	19	1949	236	1510
	20	1950	330	912
	21	1951	140	858
	22	1952	102	442
	23	1953	100	676
	24	1954	106	640
	25	1955	132	629
	26	1956	174	1000
	27	1957	256	2570
	28	1958	113	600
	29	1959	120	677
	30	1960	177	981
	31	1961	280	910
	32	1962	194	1060
	33	1963	180	1120
	34	1964	157	701
	35	1965	187	1020
	36	1966	189	914
	37	1967	72,9	320
	38	1968	110	545
	39	1969	213	721
	40	1970	347	2400

Таблица 2 - Статистическая совокупность ряда среднегодового стока р. Тура - г. Тюмень 1931-1970
интервал		61,2-121,2	121,2-181,2	181,2-241,2	241,2-301,2	301,2-361,2	361,2-421,2
число значений m		13	10	9	5	2	1
частота p=m/n		0,33	0,25	0,23	0,13	0,05	0,03

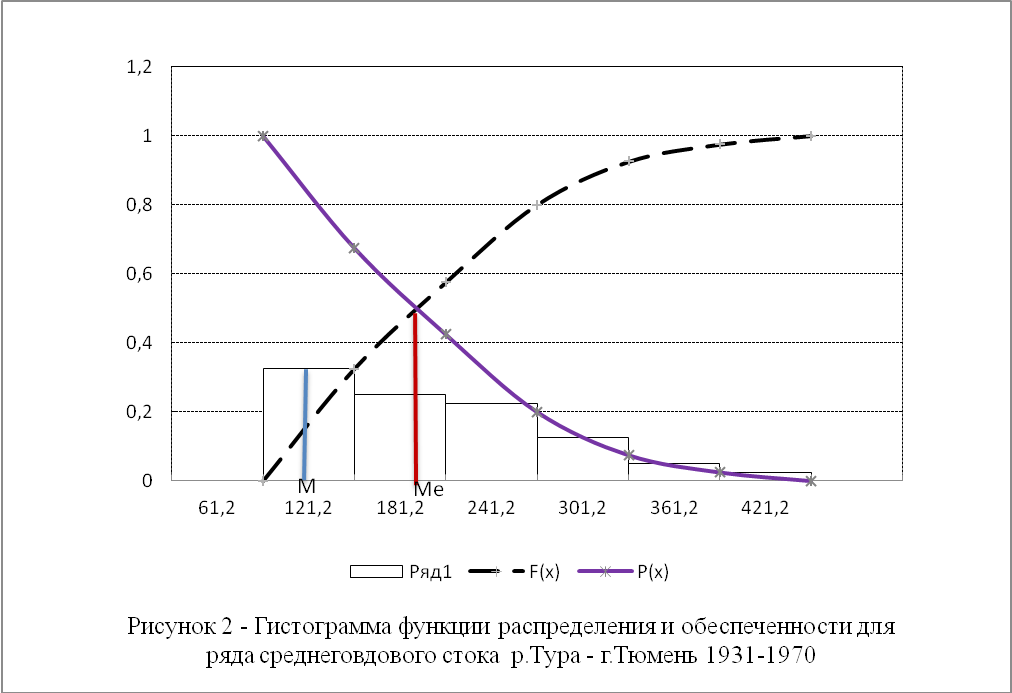
Таблица 2.1 - Статистическая совокупность ряда максимального стока р. Тура - г. Тюмень 1931-1970
интервал		320-602	602-884	884-1166	1166-1448	1448-1730	1730-2012	2012-2204	2204-2576
число значений m		9	12	11	3	2	0	1	2
частота p=m/n		0,23	0,30	0,28	0,08	0,05	0,00	0,03	0,05

Таблица 3 - Расчет эмпирических функций распределения и обеспеченности ряда среднегодового стока р. Тура - г. Тюмень 1931-1970
граница интервала х	61,2	121,2	181,2	241,2	301,2	361,2	421,2
число случаев К	0	13	23	32	37	39	40
частота F(x)=k/n	0	0,325	0,575	0,8	0,925	0,975	1
P(x)=1-F(x)	1	0,675	0,425	0,2	0,075	0,025	0

Таблица 3.1 - Расчет эмпирических функций распределения и обеспеченности ряда максимального стока р. Тура - г. Тюмень 1931-1970
граница интервала х	320	602	884	1166	1448	1730	2012	2204	2576
число случаев К	0	9	21	32	35	37	37	38	40
частота F(x)=k/n	0	0,225	0,525	0,8	0,875	0,925	0,925	0,95	1
P(x)=1-F(x)	1	0,775	0,475	0,2	0,125	0,075	0,075	0,05	0

Таблица 4 - Расчет модульных коэффициентов ряда среднегодового стока р. Тура - г.Тюмень 1931-1970
№ п\п	год	Qср , м3/с	Qср ранж	Кi	Ki-1	(Ki-1)²	(Ki-1)³	Pm
1	1911	107	417	2,32	1,320	1,742	2,29854	2,44
2	1912	237	347	1,93	0,930	0,866	0,80520	4,88
3	1913	103	330	1,84	0,836	0,698	0,58376	7,32
4	1914	61,3	300	1,67	0,669	0,447	0,29924	9,76
5	1915	151	291	1,62	0,619	0,383	0,23695	12,20
6	1916	105	286	1,59	0,591	0,349	0,20641	14,63
7	1917	147	280	1,56	0,558	0,311	0,17338	17,07
8	1918	112	256	1,42	0,424	0,180	0,07628	19,51
9	1919	79,3	237	1,32	0,318	0,101	0,03228	21,95
10	1920	132	236	1,31	0,313	0,098	0,03062	24,39
11	1921	196	220	1,22	0,224	0,050	0,01121	26,83
12	1922	220	213	1,18	0,185	0,034	0,00632	29,27
13	1923	291	196	1,09	0,090	0,008	0,00074	31,71
14	1924	182	194	1,08	0,079	0,006	0,00050	34,15
15	1925	148	189	1,05	0,051	0,003	0,00014	36,59
16	1926	286	187	1,04	0,040	0,002	0,00007	39,02
17	1927	417	182	1,01	0,012	0,000	0,00000	41,46
18	1928	300	180	1,00	0,001	0,000	0,00000	43,90
19	1929	236	177	0,98	-0,015	0,000	0,00000	46,34
20	1930	330	174	0,97	-0,032	0,001	-0,00003	48,78
21	1931	140	157	0,87	-0,127	0,016	-0,00203	51,22
22	1932	102	151	0,84	-0,160	0,026	-0,00410	53,66
23	1933	100	148	0,82	-0,177	0,031	-0,00552	56,10
24	1934	106	147	0,82	-0,182	0,033	-0,00605	58,54
25	1935	132	140	0,78	-0,221	0,049	-0,01082	60,98
26	1936	174	132	0,73	-0,266	0,071	-0,01876	63,41
27	1937	256	132	0,73	-0,266	0,071	-0,01876	65,85
28	1938	113	120	0,67	-0,332	0,111	-0,03674	68,29
29	1939	120	113	0,63	-0,371	0,138	-0,05123	70,73
30	1940	177	112	0,62	-0,377	0,142	-0,05356	73,17
31	1941	280	110	0,61	-0,388	0,151	-0,05845	75,61
32	1942	194	107	0,60	-0,405	0,164	-0,06632	78,05
33	1943	180	106	0,59	-0,410	0,168	-0,06909	80,49
34	1944	157	105	0,58	-0,416	0,173	-0,07194	82,93
35	1945	187	103	0,57	-0,427	0,182	-0,07787	85,37
36	1946	189	102	0,57	-0,433	0,187	-0,08095	87,80
37	1947	72,9	100	0,56	-0,444	0,197	-0,08736	90,24
38	1948	110	79,3	0,44	-0,559	0,312	-0,17455	92,68
39	1949	213	72,9	0,41	-0,594	0,353	-0,21008	95,12
40	1950	347	61,3	0,34	-0,659	0,434	-0,28618	97,56
сумма		179,7625		40	0	8,289	3,3713