
Вышка 3
.docx|
19.Понятие непрерывности функций нескольких переменных. Свойства непрерывных функций. Функция z = f{x;y) (или f{M)) называется непрерывной в точке Мо(хо;уо), если она: а)определена в этой точке и некоторой ее окрестности, б)имеет
предел в) этот предел равен значению функции z в точке М0, т. е.
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается, называются точками разрыва этой функции. Можно дать другое, равносильное приведенному выше, определение непрерывности функции z = f(x; у) в точке. Обозначим ∆x = x-xо, ∆у = y- уо, ∆z = f{x,у)- f(xo,yo)- Величины ∆x и ∆у называются приращениями аргументов х и у, a ∆z — полным приращением функции f(x;y) в точке Мо(хо;Уо). Функция z = f(x;y) называется непрерывной в точке М0(x0; уо) € D если выполняется равенство
|
20.Частные производные. Дифференцируемость функций нескольких переменных. Пусть задана функция z = f(x;y). Так как x и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение ∆ч, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по x и обозначается ∆xz. Итак, ∆xz=f(x +∆x; y)- f(x; y). Аналогично получаем частное приращение z по у: ∆yz=f(x; y+∆y)-f(x; y). Полное приращение ∆z функции г определяется равенством ∆z=f(x+ ∆x; y+ ∆y)-f(x; y). Если существует предел
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. |
21.Дифференциал функции нескольких переменных. Теорема о существовании полного дифференциала. Функция z=f(x;y) называется дифференцируемой в точке М(х;у) если её полное приращение в этой точке можно представить в виде: z=A*∆x+B*∆y+ +α*∆x+β*∆y, где α=α(∆x; ∆y)→0 и β=β(∆x; ∆y)→0 при ∆x→0, ∆y→0. Сумма первых слагаемых в равенстве представляет собой главную часть приращения функции. Главная часть приращения функции z=f(x; y), линейная относительно ∆x и ∆y, называется полным дифференциалом этой функции и обозначается символом dz: dz= A*∆x+B*∆y. Выражения A*∆x и B*∆y называются частными дифференциалами. Т.(достаточное условие дифференцируемости). Если функция z=f(x; y) имеет непрерывные частные производные z’x и z’y в точке М(х;у), то она дифференцируема в этой точке и её полный дифференциал выражается формулой
|
|
22.Геометрический смысл дифференцируемости функции двух переменных. Касательная плоскость и нормаль. Графиком функции z=(x; у) является некоторая поверхность. График функции z = f\x;yo) есть линия пересечения этой поверхности с плоскостью y=yo. Исходя из геометрического смысла производной для функции одной переменной , заключаем, что f'x (xo,yo)=tga, где а — угол между осью Ох и касательной, проведенной к кривой z = f(x;yo) в точке М0(х0;у0; f(x0;yo))
Составим ее уравнение. Так как плоскость а проходит через точку Мо{хо;уо; zo), то ее уравнение может быть записано в виде А(х - x0) + В{у - у0) + C(z - z0) = 0, которое можно переписать так: z - z0 = А1 (х - х0) + В1 (у - у0)- ур 45.1 |
23.Дифференцирование сложных функций нескольких переменных. Однородные функции. Теорема Эйлера о дифференцировании однородных функций. Однородная
функция степени q—
числовая функция
причём q называют порядком однородности. Свойства: 1.Если функция f является многочленом от n переменных, то она будет однородной функцией степени q в том и только в том случае, когда f — однородный многочлен степени q , в частности в этом случае q должно быть целым. 2.
Однородная функция
в нуле равна нулю, если она там
определена:
3.
Лемма Эйлера.
Однородные функции пропорциональны
скалярному произведению своего
градиента на вектор своих переменных
с коэффициентом равным порядку
однородности:
Пусть u = f (х, у) задана в области D и пусть х = х(t ) и у = у(t ) определены в области (∆) , причём, когда t€(∆) , то х и у принадлежат области D . Пусть функция u дифференцируема в точке M0 (x0, y0, z0), а функции х(t ) и у(t ) дифференцируемы в соответствующей точке t0, то сложная функция u = f [x(t), y(t)]=F (t) дифференцируема в точке t0 и имеет место равенство:
|
24.Производные высших порядков функций нескольких переменных. Смешанные производные. Теорема о смешанных производных. Дифференциалы высших порядков. Формула Тейлора для функций нескольких переменных. Частные
производные
Аналогичным способом определяются производные 3-го 4-го и т.д. порядков. Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной.
|
|
25.Экстремум функции нескольких переменных. Необходимые условия существования экстремума. Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функций одной независимой переменной. Пусть функция z = f(x; у) определена в некоторой области. точка N(x0;y()) €D. Точка (хо;уо) называется точкой максимума функции z=f(x; у), если существует такая δ-окрестность точки (хо;уо), чтобы для каждой точки (х;у), отличной от (хо;уо), из этой окрестности выполняется неравенство f{x;y) < f(x0; у0 ). Аналогично определяется точка минимума функции: для всех точек (x; у), отличных от (x0; уо), из δ-окрестности точки (xо;yо) выполняется неравенство: f(x;y) >f(x0;y0).
Значение функции в точке максимума (минимума) называется максимумом (минимумом.) функции. Максимум и минимум функции называют ее экстремумами. |
26.Квадратичная форма второго дифференциала. Достаточное условие существования экстремума функции нескольких переменных. Достаточное условие существования экстремума. Пусть в стационарной точке (х0;уо)и некоторой ее окрестности функция f(x;y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (хо;уо) значения А = f"xх(xo;yo), В = = f"yу (хo;yo), С = 1"ху(х0;уо)- Обозначим
Тогда: 1.если ∆ > 0, то функция f(x;y) в точке (хо;уо) имеет экстремум: максимум, если А < 0; минимум, если А > 0; 2. если ∆ < 0, то функция f(x; у) в точке (хо; у0) экстремума не имеет. В случае ∆ = 0 экстремум в точке (xо; у о) может быть, может не быть.
|
27.Условный экстремум. Методы поиска условного экстремума. Функция Лагранжа. Наибольшее и наименьшее значение функции неск переменных в замкнутой области. Условным экстремумом функции z = f (х, у) называется экстремум этой функции, достигнутый при условии, что переменные х и у связаны уравнением (х, у) = 0 . Метод Лагранжа. 1.Составим
функцию Лагранжа в виде линейной
комбинации функции f и функций
2.
Составим систему
из
3. Если
полученная система имеет решение
относительно параметров
|
|
_______________ |
Частные
производные
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Функция z=f(x;y) называется дифференцируемой в точке М(х;у) если её полное приращение в этой точке можно представить в виде: ∆z=A*∆x+B*∆y+ +α*∆x+β*∆y. Т.(необходимое условие дифференцируемости). Если функция z=f(x; y) дифференцируема в точке М(х;у) то она непрерывна в этой точке, имеет в ней частные производные
Т.(достаточное условие дифференцируемости). Если функция z=f(x; y) имеет непрерывные частные производные z’x и z’y в точке М(х;у), то она дифференцируема в этой точке и её полный дифференциал выражается формулой
|
Приведем свойства функций, непрерывных в ограниченной замкнутой области. Предварительно уточним понятие области. Областью называется множество точек плоскости, обладающих свойствами открытости и связности. Свойство открытости: каждая точка принадлежит ей вместе с некоторой окрестностью этой точки. Свойство связности-, любые две точки области можно соединить непрерывной линией, целиком лежащей в этой области. Точка No называется граничной точкой области D, если она не принадлежит D, но в любой окрестности ее лежат точки этой области. Совокупность граничных точек области D называется границей D. Область D с присоединенной к ней границей называется замкнутой областью, обозначается D . Область называется ограниченной, если все ее точки принадлежат некоторому кругу радиуса R. В противном случае область называется неограниченной. Примером неограниченной области может служить множество точек первого координатного угла, а примером ограниченной δ-окрестность точки М0 (хо; уо). Если функция z= f(N) непрерывна в ограниченной замкнутой области, то она в этой области: а) ограничена, т. е. существует такое число R > 0, что для всех точек N в этой области выполняется неравенство |f(N)| < R; б) имеет точки, в которых принимает наименьшее т и наибольшее М значения; в) принимает хотя бы в одной точке области любое численное значение, заключенное между т и М. |
|
Теорема 44.1 (Шварц). Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой. В
частности для z=f(x; y) имеем
Введем
понятие дифференциала высшего порядка.
Полный дифференциал функции
Аналогично
можно получить формулу для диф 3-го:
Полученные формулы справедливы лишь в случае, когда переменные х и у функции z=f(x; y) являются независимыми. F(x)= где xq = x0 + q Dx, Dx = x – x0 |
|
(разделив уравнение на –С и обозначив А1=А/-С, В1=В/-С).Найдём
А1
и В1.
Уравнения
касательных L1
и L2
имеют вид:
Касательная l1 лежит в плоскости а, следовательно, координаты всех точек 1г удовлетворяют уравнению (45.1). Этот факт можно записать в виде системы
Разрешая эту систему относительно B1, получим, что В1 = f'y (xo;yo)- Проводя аналогичные рассуждения для касательной 12, легко установить, что A1= f'x (x0 ,yo)/ Подставив значения А1 и В1 в уравнение (45.1), получаем искомое уравнение касательной плоскости:
Прямая, проходящая через точку М0 и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью. Используя условие перпендикулярности прямой и плоскости , легко получить канонические уравнения нормали:
|
|
Пусть
функция z
=
f(x;
у)
определена и непрерывна в ограниченной
замкнутой области
Правило
нахождения
наибольшего и наименьшего значений
дифференцируемой в области
|
Необходимое условие существования экстремума: Если в точке N(x0; y0) дифференцируемая функция z=f(x;y) имеет экстремум, то ее частные производные в этой точке равны нулю: f'x(xo;yo) = О, f'y (хо; y0) = 0. Зафиксируем одну из переменных. Положим, например, y=y0 получим функцию f(x; yо) = (x) одной переменной, которая имеет экстремум при х = х0. Следовательно, согласно необходимому условию экстремума функции одной переменной, (xо) = 0, т. е. f’y (x0; y0)=0 |
_________________ |

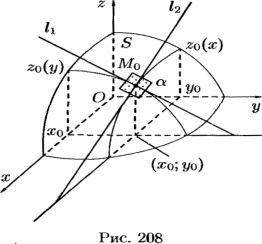 для
сечения у
= у0,
построим касательную L2
к
кривой z0
(x)
в точке х=x0.
Прямые L1
и
L2
определяют плоскость а,
которая называется касательной
плоскостью
к поверхности S
в
точке М0.
для
сечения у
= у0,
построим касательную L2
к
кривой z0
(x)
в точке х=x0.
Прямые L1
и
L2
определяют плоскость а,
которая называется касательной
плоскостью
к поверхности S
в
точке М0.
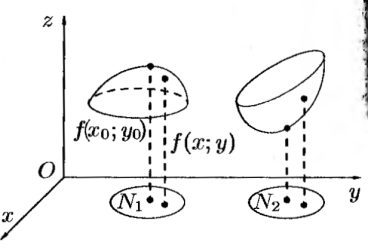 N1-точка
max,
N2-точка
min
N1-точка
max,
N2-точка
min