9

Работа № М-3

Изучение законов вращательного движения с помощью маятника Обербека

1. Общие сведения

Целью настоящей работы является исследование законов вращательного движения твердого тела на примере маятника Обербека. В работе определяется момент инерции маятника Обербека.

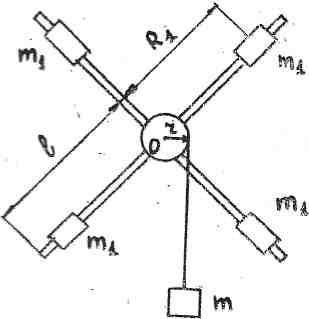
Рис1

Маятник Обербека представляет собой крестовину, состоящую из четырех стержней длиной L, расположенных под прямым углом друг к другу и прикрепленных к шкиву радиусом r (рис1). Шкив способен вращаться вокруг неподвижной горизонтальной оси O, На стержни надеваются четыре одинаковых груза массой m₁ каждый, которые можно перемещать вдоль стержней и закреплять на определенном расстоянии R₁ от оси вращения. Грузы закрепляются симметрично, т.е. так, чтобы их центр масс совпадал с осью вращения. На шкив наматывается нить , к свободному концу которой прикрепляется груз массой m. Под действием этого груза нить разматывается и приводит маятник в равноускоренное вращательное движение.

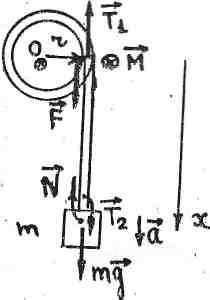
Рис.2

Применим основное уравнение вращательного движения твердого тела относительно неподвижной оси Iε_Ζ=M_Z….(1) к маятнику Обербека. Пренебрежем силами трения, действующими на маятник. Тогда вращательный момент будет создаваться только силой ,возникающей в результате натяжения нити. Плечо силы равно r, а момент силы относительно оси О, направленной от нас за плоскость чертежа (на рис 2 такое направление оси условно обозначено 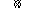), равен rF. Тогда уравнение (1) для маятника Обербека принимает вид

Iε=Fr,…..(2) ,

где I – момент инерции маятника относительно неподвижной оси,ε – угловое ускорение.

По третьему закону Ньютона сила равна по модулю силе натяжения нити т.е. . Если считать нить невесомой, то силы натяжения нити и равны по модулю. По третьему закону Ньютона сила натяжения нити равна по модулю силе упругости , действующей на груз со стороны нити, так что

……….(3)

На груз ,кроме силы упругости , действует сила тяжести m (см. рис. 2),Поэтому основное уравнение динамики поступательного движения груза вдоль оси x (второй закон Ньютона) может быть записан в виде

ma=mg – N,…….(4)

где а – ускорение груза, g – ускорение свободного падения (g=9,8).

Если нить не проскальзывает при движении по блоку, то угловое ускорение ε связано с линейным ускорением а соотношением

a = r ε (5)

Если груз движется равноускоренно с нулевой начальной скоростью и ускорением а, то за время t груз пройдет путь

………..(6)

Решая систему уравнений (2)-(6) относительно величины I, получим следующее выражение для момента инерции маятника относительно оси вращения:

I_эксп. = , (7)

где D – диаметр шкива

Таким образом, для экспериментального определения момента инерции маятника Обербека необходимо измерить следующие величины:

1 m – масса груза, приводящего маятник во вращательное равномерное движение;

2 D диаметр шкива;

3 t –время движения груза;

4 h – расстояние, пройденное грузом за это время

Теоретический расчет момента инерции маятника Обербека

Момент инерции маятника Обербека относительно оси вращения может быть рассчитан путем суммирования моментов инерции шкива, четырех стержней и четырех грузов, укрепленных на стержнях

I_T = I₀ + 4, (8)

где I₀ – момент инерции шкива относительно оси вращения, - момент инерции крестовины (четырех стержней) без грузов, l – длина стержня крестовины, m₂ – масса стержня без груза, 4m₁R² – момент инерции грузов крестовины, R – расстояние от оси вращения до центра масс грузов, m₁ – масса груза на стержне.

Формула (8) справедлива в том случае, когда размеры грузов на стержнях малы по сравнению с расстоянием R. Если пренебречь моментом инерции шкива, то формула (8) преобразуется таким образом

I_T = .

2.-Экспериментальная установка

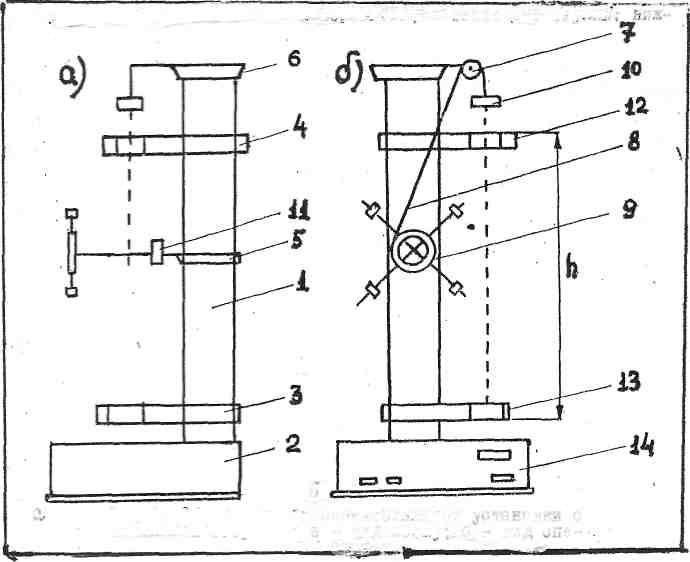
Рис.3

Общий вид маятника Обербека приведен на рис. 3. На вертикальной штанге 1, установленной на основании 2, закреплены два кронштейна: нижний 3 и верхний 4, а также две втулки: нижняя 5 и верхняя 6. На верхней втулке 6 помещен диск 7. Через диск перекидывается нить 8, один конец которой прикреплен к шкиву 9, а на втором конце нити расположены грузы массой m.На нижней втулке закреплен электромагнитный тормоз 11, который после подключения к нему питающего напряжения удерживает систему крестовины вместе с грузами в состоянии покоя.

На кронштейне 4 закреплен фотоэлектрический датчик 12, вырабатывающий электрический импульс о начале движения системы. На кронштейне 3 установлен фотоэлектрический датчик 13, вырабатывающий импульс после прохождения грузами 10 пути h. На основании 2 закреплен секундомер 14. Он запускается импульсом датчика 12 и останавливается импульсом датчика 13, измеряя тем самым время t прохождения грузами 10 пути h.

На передней панели секундомера расположены два выключателя с лампочками. Один из них включает напряжение питания «12в» (при этом загорается красная лампочка). Другой отключает тормоз (зеленая лампочка) Кроме того , там же на передней панели находится цифровое табло секундомера и две кнопки «пуск» и «сброс» При включении напряжения питания «12в» на табло должна высвечиваться цифра «0», а на электромагнитный тормоз 11 подается питающее напряжение (тормоз включен, зеленая лампочка не горит) При нажатии кнопки «сброс» происходит обнуление показаний индикаторов. При нажатии кнопки «пуск» электромагнитный тормоз освобождает систему и она приходит в движение.