Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Рязанский государственный радиотехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

10 блок_ Шуляков_планирование эксперимента / Метод исключения _Многомерные методы поиска экстремума

.pdf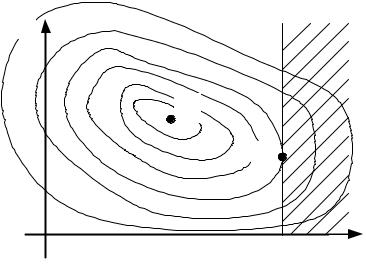

Скачиваний:

Добавлен:

15.04.2015

Размер:

103.33 Кб

Скачать

☆

Многомерные методы поиска экстремума
Метод исключения
Метод исключения предполагает последовательное отсечение отдельных
частей области эксперимента плоскостями, касательными к поверхностям
уровня.
x2		Пусть на какой либо
x2		поверхности уровня выбрана
		опорная точка А с
		координатами XA, через
Х*		которую прошла касательная
Х*		гиперплоскость, разделившая
ХA		область эксперимента на две
ХA		подобласти. Если y = f (X )
		строго унимодальна, то
		оказывается возможным
0	x1	отделить подобласть с более
0	x1	высокими значениями y от
		подобласти с меньшими у. В
результате образуется новая область неопределенности и к ней вся процедура
исключения повторяется. Сделав несколько таких шагов, можно приблизится к
X * .
В данном случае справедливо утверждение: если max строго
унимодальной функции y = f (X )	достигается в точке X* = (x1, x2,..., xn *) ,
то для любой точки X A = (x1A , x2 A ,..., xnA ) из области эксперимента
справедливо соотношение:

n	æ	¶f	ö
åç		¶f	÷	(xi *-xiA ) ³ 0 .
åç		¶x	÷	(xi *-xiA ) ³ 0 .
i=1	è	i øX A

n	æ	¶f	ö
Учитывая, что åç		¶f	÷	(xi - xiA ) = 0 – есть уравнение
Учитывая, что åç		¶x	÷	(xi - xiA ) = 0 – есть уравнение
i=1	è	i øX A

гиперповерхности, касательной к поверхности уровня в точке X A , точка

экстремума X * всегда находится по одну сторону от касательной. Достоинства: простота процедуры, на основании только одного

исследования окрестности очередной опорной точки отбрасывается целая бесперспективная подобласть.

Недостатки:

∙применение только для строго унимодальных функций;

∙чувствительность к погрешностям эксперимента.

Пример: Найти значения переменных x1, x2, x3, при которых достигается

максимум

строго

унимодальной

функции

y = e−(0,1x12 +0,4x22 +0,9x32 ) , при

условии 0 £ xi £ 3 , i = 1,3 , ε = 0,05.

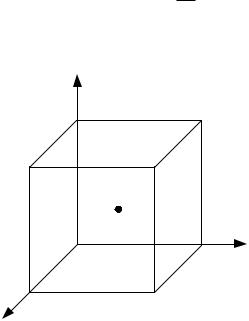
1) Область

эксперимента

данном

случае

является

куб.

Выберем

в качестве

начальной

опорной точки среднюю точку куба Xс

x1c

= 1,5

(центр куба), с координатами: x2c

= 1,5 .

x3c

= 1,5

Значения функции отклика в этой

точке

= e

−3,15

. Проводим группу

пробных

экспериментов

точках:

X1c = (1,55;1,5;1,5)

X 2c = (1,5;1,55;1,5) .

X 3c = (1,5;1,5;1,55)

	æ	¶f	ö
	ç		÷

Для оценки производных	ç		÷	и составления уравнения
	è	¶xi øXc

касательной.

Результаты этих экспериментов являются:

= e−3,17

= e−3,21

= e−3,29

Из последнего получаем:

¶f

−3,17

-e

−3,15

−2

= -1,6×10

;

¶x1

0,05

øXc

¶f

−2

;

¶x2

= -5×10

øXc

¶f

−2

¶x3

= -11×10 .

øXc

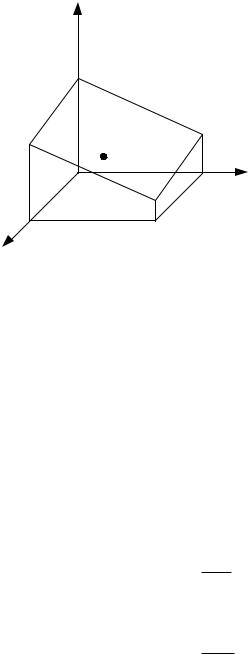
Отсюда следует уравнение касательной:

y =1,6(x1 − x1c ) + 5(x2 − x2c ) +11(x3 − x3c ) = 0 .

Для дальнейшего рассмотрения интерес представляют точки, удовлетворяющие условию:

Dy ³ 0 ,

которое вместе с исходными уравнениями:

0 £ xi £ 3

дает возможность указать новую область неопределенности, оставшуюся после проведенного первого исключения.

		x3
	2,45
1,9		1
1,9		Xц	x2
	0	3	x2
	0	0,5
		0,5
3

2) Использование средней точки в

качестве центра области оказалось удачным (отброшена почти половина первоначальной области эксперимента). Поэтому, начиная второй шаг будем вновь ориентироваться на среднюю точку, как на новый центр (введем обозначение Xц):

x1ц		=1,5		y	= e−2,42
x	2ц	=1,5	,
		=1,2		ц	.
x3ц

Попутно заметим, что yц > yc , т.е.

движение идет в правильном направлении.

Делаем пробные эксперименты:

X1ц = (1,55;1,5;1,2)

X 2ц = (1,5;1,55;1,2)

X 3ц = (1,5;1,5;1,25)

y1ц = e−2,44 y2ц = e−2,49 y3ц = e−2,53

Отсюда находим уравнение новой касательной:

æ ¶f ö ç ÷ çè ¶x1 ÷øXц

æ ¶f ö ç ÷ çè ¶x2 ÷øXц

=-3,4×10−2 ;

=-12×10−2 ;

æ	¶f	ö	−2
ç	¶f	÷
ç		÷
ç	¶x3	÷	= -18,4×10 .
è	¶x3	øXц

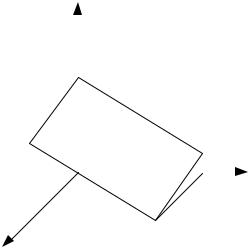
y = 3,4(x1 − x1ц ) +12(x2 − x2ц ) +18,4(x3 − x3ц )

Как и в предыдущем случае условия: Dy ³ 0 ; 0 £ xi £ 3 позволяют

прийти

новой

области

неопределенности.

Как

видно,

второе

исключение

оказалось

не

таким

2,45

эффективным, как первое. Причина:

смещение точки Xц к периферии области

эксперимента. В этом заключается один

из скрытых

недостатков

использования

1,9

0,5

средней

точки

в качестве

центра.

3 x2

Поэтому на третьем шаге нужно ввести

определенные коррективы.

Пусть

центром

оставшейся

области

неопределенности,

имеющей

объем V, будет ее центр тяжести Xцт,

координаты которого:

Vò

X1цт =

x1dV ;

X1цт =1,38;

X 2цт =

Vòx2dV ;

X 2цт =1,09 ;

V Vò

X 3цт =

x3dV ;

X 3цт = 0,73;

y = e−1,15

цт

Тогда точки проведения пробных экспериментов:

X1цт = (1,43;1,09;0,73)

= e−1,17

1цт

= e−1,19

X 2цт = (1,38;1,14;0,73)

2цт

= e−1,22

X 3цт = (1,38;1,09;0,78)

3цт

æ ¶f ö

çè ¶x1 ÷øXцт

æ ¶f ö ç ÷ çè ¶x2 ÷øXцт

æ ¶f ö ç ÷ çè ¶x3 ÷øXцт

Уравнение новой касательной:

=-12,4×10−2 ;

=-24,8×10−2 ;

=-42,8×10−2 .

y =12,4(x1 − x1цт ) + 24,8(x2 − x2цт) + 42,8(x3 − x3цт ) = 0

			x3		Условия	Dy ³ 0 ;
			x3		Условия	Dy ³ 0 ;
					0 £ xi £ 3 позволяют получить новую
					область неопределенности, т.е. выбор
	1,7				центра тяжести оправдал себя.
	1,7				Прежде, чем сделать следующий
					шаг имеет смысл проанализировать то,
		0		3 x2	что достигнуто. При переходе из Xc в Xц
0,9					и далее в Хцт значения y возрастали и


3					наиболее существенное увеличение у
					произошло на переходе Хц→Хцт.
	1,5				произошло на переходе Хц→Хцт.
x1	1,5				Рассмотрим произвольную точку
					Х на продолжении отрезка	[Хц, Хцт],

предполагая что это будет продолжение строго возрастающей прямолинейной

траектории, идущей к Х*.

Учитывая,

что хiцт<хiц исследуем

те точки, координаты которых связаны

с координатами Xц и Хцт следующими

соотношениями:

i =

xiцт = axiц + (1− a)xi ,

, a

1,3

–

Xц

параметр

(0<a<1),

показатель

отношения в котором точка Хцт делит

Xцт

отрезок [Х, Хц],

a =

xiцт − хi

. Поскольку

xiц −

хi

именно таким Х={xi} будут отвечать

величины y>yцт. Очевидно, что прямая,

продолжающая

отрезок

[Хц, Хцт]

содержащая точку Х, должна где-то пересечь границу области, полученной на третьем шаге. При этом будет либо х1=0, либо х2=0, либо х3=0.

	Полагая в равенстве, связывающем Xц, Хцт, Х поочередно равными нулю
х1, х2,		х3,	получаем из него три значения			а,	меньшее	из		которых, т.е.
~		ì		ü
~		ï xiцт ï
a	= miní			ý определяет искомую точку	пересечения			X		= (1,17;0,45;0) .
a	= miní			ý определяет искомую точку	пересечения			X		= (1,17;0,45;0) .
	i	ï x	ï						П
		î	iц þ
Проводя в точке Х эксперимент, т.е. получив					y	П	= e-0,22 , убеждаемся в том, что
				П		П

действительно существует прямолинейная строго возрастающая траектория, проходящая через Xц, Хцт, ХП однако вопрос о местонахождении Х* остается пока открытым.

4) Поскольку наибольшим из всех полученных значений у является уП,

можно принять точку ХП за новый центр группы пробных экспериментов и провести все необходимые операции:

æ ¶f ö ç ÷ çè ¶x1 ÷øXП

æ ¶f ö ç ÷ çè ¶x2 ÷øXП

æ ¶f ö ç ÷ çè ¶x3 ÷øXП

X1П = (1,22;0,45;0)		y1П = e−0,23
X 2П = (1,17;0,5;0)		y2П = e−0,24
X 3П = (1,17;0,45;0,05)		y	= e−0,24
X 3П = (1,17;0,45;0,05)		3П
= -16×10−2	;
= -32×10−2	;
= -32×10−2	.
	.

Уравнение касательной плоскости:

y =16(x1 − x1П ) +32(x2 − x2П ) +32(x3 − x3П ).

	x3				Учитывая,	что	Dy ³ 0 ,
	x3				Учитывая,	что	Dy ³ 0 ,
				0 £ xi £ 3 , получим новую область
				неопределенности,		которая	составляет
1,04				от предыдущей всего 40%, что является
1,04				следствием анализа обстановки перед
				четвертым шагом.
	0	1,04	x2		Но теперь выяснилось, что ХП не
2,08				есть Х*. Обратим внимание на тот факт,
				есть Х*. Обратим внимание на тот факт,
				что	в процессе переходов		от одной

опорной точки к другой их координаты не увеличивались, т.е.

xic ³ xiц ³ xiцт ³ xiП .

В этой ситуации есть смысл проверить точку X0 = (0,0,0) , которая к тому

же является крайней в области эксперимента. Вычисляем у0=1. Все предшествующие были меньше, поэтому можно предположить, что Х0=Х*; у*=1

иперейти к заключительному этапу.

5)Прежде всего, необходимо построить простейшую аппроксимирующую формулу (модель поверхности отклика в окрестности Х*). Для этого находим значения у при обычных приращениях хi:

X10	= (0,05;0;0) ;	y10 = e-2,510× −4
X20	= (0;0,05;0) ;	y20 = e-10×10−4
X30	= (0;0;0,05) ;	y30 = e-2210× −4	,

а также значения у при удвоенных приращениях xi:

X ′	= (0,1;0;0)	;	y′	= e-1010× −4
10		;	10
X ′	= (0;0,1;0)	;	y′	= e-40×10−4
20		;	20
X ′	= (0;0;0,1)	;	y′	= e-9010× −4
30		;	30	,

Находим оценки производных

æ ¶f ö çè ¶x1 ÷øX *

æ ¶f ö çè ¶x2 ÷øX *

æ ¶f ö çè ¶x3 ÷øX *

;-0,5×10−2 ;

;-2×10−2 ;

;-4,5×10−2 ;

æ	¶	2	f	ö	; -0,2
ç	¶		f	÷	; -0,2
è	¶x12			øX *
æ	¶	2	f	ö	; -0,8
ç	¶		f	÷	; -0,8
è	¶x22			øX *
æ	¶	2	f	ö	; -1,8
ç	¶		f	÷	; -1,8	.
			2	øX *		.
è ¶x3				øX *

Эти оценки выступают в роли коэффициентов формуле модели:

Dукв = -(0,5Dх1 + 2Dх2 + 4,5Dх3 ) ×10−2 - 12 (0,2Dх12 + 0,8Dх22 +1,8Dх32 )

Далее составляется система уравнений:

d ( yкв )

= 0,5×10−2 + 0,2Dx1 = 0 ;

d (Dx1)

d ( yкв )

= 2 ×10−2 + 0,8Dx2

= 0 ;

d (Dx2 )

d ( yкв )

= 4,5×10−2 +1,8Dx3

= 0 .

d (Dx3 )

Решение

этой

системы:

х1 = х2 =

х3 = 0,025

удовлетворяет

неравенствам

Dхi

< ε . Таким образом, формула для укв может быть признана

допустимой, тем более, что

укв = F(

xi )

является отрицательно определенной

в условиях

рассматриваемой

задачи;

поэтому

вопрос о

замене точки

X * = (0,0,0) на точку X ** = (0,025;0,025;0,025) не возникает.

Вывод: точка X * = (0,0,0) ; у* =1 – является точкой экстремума.

Соседние файлы в папке 10 блок_ Шуляков_планирование эксперимента

#
15.04.2015248.84 Кб367.jpg
#
15.04.2015157.79 Кб41Активные стратегии одномерного поиска.pdf
#
15.04.2015103.33 Кб42Метод исключения _Многомерные методы поиска экстремума.pdf
#
15.04.201588.05 Кб40Метод конфигураций.pdf
#
15.04.2015312.21 Кб45Методы многомерного поиска экстремума.pdf
#
15.04.2015483.05 Кб60Методы случайного поиска экстремума.pdf
#
15.04.2015292.46 Кб47Промышленные эксперименты.pdf