
Жулев_3_4_9_15_16_20
.pdf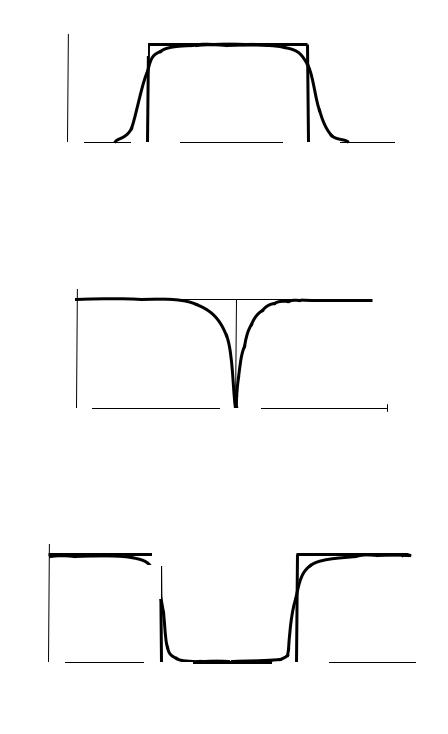
Т(ω)
1
2
ω
0 |
ωс1 |
ωс2 |
1 – идеальная АЧХ; 2 – реальная АЧХ Рис. 5.3.
г) режекторный фильтр или фильтр-«пробка» (рис. 5.4);
Т(ω)
ω
0 |
ωр |
|
Рис. 5.4. |
д) полосно-пропускающий фильтр (рис. 5.5).
Т(ω)
1
2
ω
0 |
ωс1 |
ωс2 |
1 – идеальная АЧХ; 2 – реальная АЧХ Рис. 5.5.
Реально нельзя получить идеальные формы частотных характеристик в виде прямоугольников со строго постоянным коэффициентом передачи в полосе пропускания, бесконечным ослаблением в полосе подавления и бесконечной крутизной спада при переходе от полосы пропускания к полосе подавления. Между полосой пропускания и полосой подавления реально существует переходная полоса, а АЧХ в полосе пропускания и полосе подавления имеет некоторую неравномерность (рис. 5.6).

Т(ω)
Т0
∆Т
переходная полоса
полоса пропускания |
полоса задержки |
Тз
ω
0 |
|
ωс |
ωз |
|
|
|
|
|
|
|
|
Рис. 5.6.
На рис. 5.6 приняты следующие обозначения:
-Т0 – номинальный коэффициент передачи в полосе пропускания (0 ≤ ω ≤ ωс),
-∆Т – неравномерность коэффициента передачи в полосе пропускания,
-Тз – номинальный коэффициент передачи в полосе задерживания (ωз ≤ ω ≤ ∞).
При проектировании фильтра требования к его АЧХ обычно задают графиком допусков. Например, график допусков для полосового фильтра изображен на рис. 5.7.
Т(ω)
Т0 

∆Т
Тз
ω
0 |
|
ωз1 |
|
ωс1 |
|
ωс2 |
|
ωз2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.7.
В ряде случаев кроме указанных требований к АЧХ также накладывают ограничения на ФЧХ и временные характеристики фильтра.
Фильтры бывают пассивными (RC-фильтры и LC-фильтры) и активными (ARCфильтры). Наиболее популярными аналоговыми фильтрами являются активные RCфильтры.
Активные RC-фильтры относят к классу линейных электрических цепей с

сосредоточенными и постоянными во времени параметрами, передаточная функция которых имеет следующий вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
T(p) = |
U |
|
(p) |
= |
N(p) |
= |
b |
m |
p |
m |
+ b |
m−1 |
p |
m−1 |
+ + b |
0 |
= K |
∏(p − zi ) |
, |
вых |
|
|
i=1 |
||||||||||||||||
|
|
D(p) |
|
|
|
|
|
|
|
|
|||||||||
|
Uвх(p) |
|
|
an pn |
+ an−1 |
pn−1 + + a0 |
|
n |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∏(p − pi ) |
|
i=1
где Т(р) – передаточная функция схемы,
Uвх(p) и Uвых(p) – изображения по Лапласу входного и выходного напряжений соответственно,
p=σ+j ω – комплексная переменная,
bi, ai – вещественные коэффициенты, зависящие от параметров цепи, К – масштабирующий множитель,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n – порядок цепи ( n > m). |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Корни |
pi |
характеристического уравнения D(p)=0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
j ω |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
zi |
|
|
|
|
|
|
называются полюсами передаточной функции, а корни |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
ωz |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zi |
характеристического уравнения N(p)=0 называются |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
pi |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωp |
|
|
нулями передаточной функции. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
|
рассматриваемых |
активных |
RC-фильтров |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|||||||||||
|
|
|
σp |
σz |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
полюса |
|
pi |
находятся в |
левой |
полуплоскости |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
-ωp |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
комплексной переменной p. |
|
|
|||||||||||||
|
|
pi |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Графическое изображение полюсов и нулей в |
|||||||||||||
|
|
|
|
|
|
|
|
|
-ωz |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
zi |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
плоскости комплексной переменной p называют картой |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
Рис. 5.8. |
особых точек или полюсно-нулевой картой (рис. 5.8). |
||||||||||||||||||||
|
|
|
|
|
|
|
В общем случае полюсы являются комплексными: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi = σp ± j ωp . |
|
|
|||||||||
Они характеризуются частотой |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
= |
|
p |
i |
|
= |
|
σ2 |
+ ω2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
p |
p |
|
|
||
и добротностью
Q0 = 2ωσp p .
Частота ωz и добротность Qz определяются аналогично.
Особые точки физически реализуемых цепей являются действительными и образуют

комплексно-сопряженные пары, симметричные относительно оси σ. Поэтому обычно изображают только верхнюю полуплоскость p.
Все характеристики линейной цепи определяются коэффициентами ai, bi и полюсами pi и нулями zi передаточной функции.
АЧХ является зависимостью модуля передаточной функции T(p) от частоты:
|
|
|
|
|
|
|
|
|
m |
|
|
|||||
T(ω) = |
|
T(p) |
|
= |
|
T(j ω) |
|
= K |
∏ |
|
|
j ω − zi |
|
. |
||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
i=1 |
|
|
|
|
|
|||||||
|
|
|
|
|||||||||||||
|
|
|
|
n |
|
|||||||||||
|
|
|
|
|
|
|
|
|
∏ |
|
j ω −pi |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|||||
Если коэффициент передачи в полосе пропускания равен постоянному значению Т0, то АЧХ фильтра удобно представить в виде зависимости относительного затухания (в дБ) от частоты:
a(ω) = 20 |
|
T |
|
= 10 lg[1+ ε2 |
|
F(ω) |
2 |
], |
lg |
0 |
|
|
|
||||
|
|
|||||||
|
T(ω) |
|
|
|
|
|
||
где ε – коэффициент, характеризующий неравномерность коэффициента передачи в полосе пропускания,
F(ω) – функция фильтрации.
ФЧХ выражает зависимость аргумента передаточной функции от частоты:
m
φ(ω) = ∑arg(j ω − zi ) − arg(j ω − pi ) .
i=1
Переходная (импульсная) характеристика h(t), представляющая собой реакцию цепи на воздействие в виде единичного скачка, определяется как обратное преобразование Лапласа от функции T(p)/p и имеет вид
− |
T(p) |
|
N(0) |
n |
N(p |
) |
|
|
||
h(t) = L 1 |
|
|
|
= |
|
+ ∑ |
i |
|
epi |
t . |
p |
D(0) |
′ |
|
|||||||
|
|
|
|
i=1 |
pi D (pi ) |
|
|
|||
Данное выражение справедливо для цепей, не имеющих кратных полюсов.
Реальные характеристики фильтров из-за отклонения параметров элементов при воздействии дестабилизирующих факторов (температура, влажность, давление, старение) и из-за технологических допусков отличаются от требуемых.
Наиболее общей мерой для оценки изменения некоторой функции F при вариации параметров является классическая дифференциальная чувствительность первого порядка, которая определяется выражением
SFx = ∂∂Fx //Fx = ∂∂Fx Fx = ∂∂(ln(lnFx)) .
Простые ARC-фильтры также являются системами второго порядка. Их передаточная
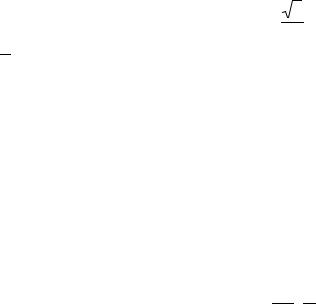
функция определяется выражением
T(p) = |
K |
= |
K |
. |
|
n |
|||
|
D(p) |
|
||
|
∏(p −pi ) |
|
||
|
|
|
i=1 |
|
Так как система имеет второй порядок, то в знаменателе одна комплексно-сопряженная пара полюсов при частоте полюса ω0.
D(p)=p2+a p+b при p=j ω, тогда добротность определяется выражением
Q = ab ,
где 
 b = ω0 .
b = ω0 .
Добротности фильтров делятся на три группы:
1)малые добротности (Q < 2);
2)средние добротности (2 ≤ Q ≤ 20);
3)большие добротности (Q > 20).
Для звеньев второго порядка традиционно используется косвенный критерий стабильности характеристик – чувствительность добротности и частоты особых точек к изменению параметра x. Например, для полюсов
SQx = ∂∂Qx Qx ,
Sωx 0 = |
∂ω0 |
|
x |
. |
∂x |
|
|||
|
|
ω0 |
||
