
Случайные величины
.docxОбщие понятия
Случайное
событие является качественной
характеристикой случайного результата
испытания, но его можно
характеризовать
количественно, этой количественной
характеристикой случайного результата
испытания
является случайная
величина.
Определение
1. Случайная
величина -
это вещественная функция, определенная
на множестве исходов,
соответствующих
данному испытанию.
То есть каждому
исходу ![]() множества
множества ![]() -
всех исходов испытания ставится
в
соответствие некоторое действительное
число
-
всех исходов испытания ставится
в
соответствие некоторое действительное
число ![]() .
Случайные
величины обозначаются
.
Случайные
величины обозначаются ![]() ;
их возможные значения
обозначаются
;
их возможные значения
обозначаются ![]() .
Рассматриваются
два типа случайных величин.
Определение
2. Дискретной
случайной величиной называется
случайная величины, число значений
которой
конечно или бесконечно,
но счетно.
Пример
1. Производится
три выстрела по мишени. Пусть случайная
величина
.
Рассматриваются
два типа случайных величин.
Определение
2. Дискретной
случайной величиной называется
случайная величины, число значений
которой
конечно или бесконечно,
но счетно.
Пример
1. Производится
три выстрела по мишени. Пусть случайная
величина ![]() -
число попаданий при трех
выстрелах.
Она может принимать значения 0,1,2,3, то
есть - это дискретная случайная
величина.
Пример
2. Производятся
выстрелы по мишени. Пусть случайная
величина
-
число попаданий при трех
выстрелах.
Она может принимать значения 0,1,2,3, то
есть - это дискретная случайная
величина.
Пример
2. Производятся
выстрелы по мишени. Пусть случайная
величина ![]() -
число выстрелов до первого
попадания.
Она может принимать значения 1,2,3,..., то
есть число значений бесконечно, но
счетно, значит это
дискретная
случайная величина.
Определение
3. Непрерывной
случайной величиной называется
случайная величина, значения
которой
занимают некоторый
интервал(конечный или бесконечный).
Пример
3. Автобус
некоторого маршрута ходит по расписанию
с интервалом 15 минут. Пусть
случайная
величина
-
число выстрелов до первого
попадания.
Она может принимать значения 1,2,3,..., то
есть число значений бесконечно, но
счетно, значит это
дискретная
случайная величина.
Определение
3. Непрерывной
случайной величиной называется
случайная величина, значения
которой
занимают некоторый
интервал(конечный или бесконечный).
Пример
3. Автобус
некоторого маршрута ходит по расписанию
с интервалом 15 минут. Пусть
случайная
величина ![]() -
время ожидания пассажиром автобуса.
Это непрерывная случайная величина, ее
значения
занимают отрезок
-
время ожидания пассажиром автобуса.
Это непрерывная случайная величина, ее
значения
занимают отрезок ![]() .
Пример
4. Работает
некоторый прибор. Пусть случайная
величина
.
Пример
4. Работает
некоторый прибор. Пусть случайная
величина ![]() -
время безотказной работы данного
прибора.
Это непрерывная случайная величина,
значения которой занимают
промежуток
-
время безотказной работы данного
прибора.
Это непрерывная случайная величина,
значения которой занимают
промежуток ![]() .
Вопрос. Бросается
игральная кость. Выпадение " шестерки"
- это:
а) дискретная случайная величина;
б)
непрерывная случайная величина;
в)
случайное событие;
г) неслучайная
величина.
.
Вопрос. Бросается
игральная кость. Выпадение " шестерки"
- это:
а) дискретная случайная величина;
б)
непрерывная случайная величина;
в)
случайное событие;
г) неслучайная
величина.
 а)
а)
 б)
б)
 в)
в)
 г)
г)
Закон распределения дискретной случайной величины
Определение 4. Законом распределение случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. Способы или формы представления закона распределения могут быть различными. Закон распределения дискретной случайной величины можно задать с помощью ряда распределения. Рядраспределения - это таблица значений случайной величины и вероятностей, с которыми эти значения принимаются.
|
|
|
|
...... |
|
|
|
|
|
...... |
|
Для
того, чтобы подобная таблица являлась
рядом распределения дискретной случайной
величины, необходимо
выполнение
следующих условий:
1. значения случайной
величины должны быть указаны в возрастающем
порядке;
2. ![]() (
если множество возможных значений
случайной величины
(
если множество возможных значений
случайной величины ![]() бесконечно,
но счетно, то ряд
бесконечно,
но счетно, то ряд
![]() должен
сходиться и его сумма должна равняться
1).
Для наглядности ряд распределения
можно изобразить графически в
виде многоугольника
распределения,
который
представляет из себя ломаную, соединяющую
точки с координатами
должен
сходиться и его сумма должна равняться
1).
Для наглядности ряд распределения
можно изобразить графически в
виде многоугольника
распределения,
который
представляет из себя ломаную, соединяющую
точки с координатами ![]() .
.
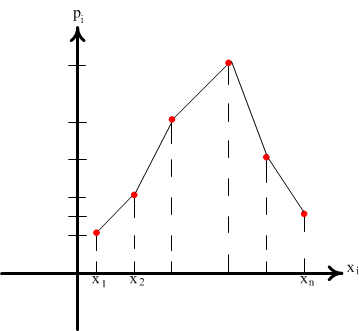
Рис.1
Пример
5.Производится
три выстрела по мишени. Вероятность
попадания при одном выстреле равна
0,7.
Пусть случайная величина ![]() -
число попаданий при трех выстрелах.
Построить ряд распределения
данной
случайной величины.
Решение. Данная
случайная величина может принимать
следующие значения: 0,1,2,3. Найдем
вероятности,
с которыми эти значения
принимаются, они вычисляются по формуле
Бернулли:
-
число попаданий при трех выстрелах.
Построить ряд распределения
данной
случайной величины.
Решение. Данная
случайная величина может принимать
следующие значения: 0,1,2,3. Найдем
вероятности,
с которыми эти значения
принимаются, они вычисляются по формуле
Бернулли:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
Теперь
построим ряд распределения:
;
Теперь
построим ряд распределения:
|
Вопрос. Данная таблица является рядом распределения.
|
|
1 |
3 |
4 |
6 |
|
|
0,15 |
0,2 |
0,25 |
0,3 |
 верно
верно
 неверно
неверно
Функция распределения вероятностей
Для
непрерывной случайной величины нельзя
построить ряд распределения, так как
она может принимать
бесконечное
число значений из некоторого промежутка,
кроме того, каждое отдельное значение
обычно не
обладает никакой отличной
от нуля вероятностью. Для непрерывной
случайной величины нужен другой
способ
задания закона
распределения.
Общей формой задания
закона распределения случайной величины
является функция
распределения вероятностей.
Определение
5. Функцией
распределения вероятностей случайной
величины ![]() называется
функция
называется
функция ![]() ,
определяющая
вероятность того, что в результате
испытания случайная величина
,
определяющая
вероятность того, что в результате
испытания случайная величина ![]() примет
значение,
меньшее
примет
значение,
меньшее ![]() .
.
![]() (1)
(1)
Геометрически равенство
означает, что если случайная величина
- это случайная точка на числовой оси,
то
![]() -
это вероятность того, что в результате
испытания случайная точка будет
расположена левее точки
-
это вероятность того, что в результате
испытания случайная точка будет
расположена левее точки ![]() .
Функцию
распределения еще принято называть
интегральным законом распределения.
Из
определения следует, что функция
распределения существует и для дискретных
случайных величин, и для
непрерывных.
Для дискретных случайных величин формула
(1) может быть записана следующим
образом:
.
Функцию
распределения еще принято называть
интегральным законом распределения.
Из
определения следует, что функция
распределения существует и для дискретных
случайных величин, и для
непрерывных.
Для дискретных случайных величин формула
(1) может быть записана следующим
образом:
![]() (2)
(2)
Свойства функции распределения.
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]() -
неубывающая функция, то есть если
-
неубывающая функция, то есть если ![]() ,
то
,
то ![]() .
С
помощью функции распределения можно
найти вероятность попадания случайной
величины на некоторый
промежуток по
формуле:
.
С
помощью функции распределения можно
найти вероятность попадания случайной
величины на некоторый
промежуток по
формуле:
![]() (3)
(3)
Так как ![]() ,
то формула (3) верна
для всех этих
случаев.
Пример
6. По
мишени производится 3 выстрела. Вероятность
попадания при одном выстреле 0,7.
Найти
функцию распределения вероятностей
случайной величины
,
то формула (3) верна
для всех этих
случаев.
Пример
6. По
мишени производится 3 выстрела. Вероятность
попадания при одном выстреле 0,7.
Найти
функцию распределения вероятностей
случайной величины ![]() -
числа попаданий при трех выстрелах.
Решение. В
примере 5 для данной случайной величины
был получен ряд распределения:
-
числа попаданий при трех выстрелах.
Решение. В
примере 5 для данной случайной величины
был получен ряд распределения:
|
|
0 |
1 |
2 |
3 |
|
|
0,027 |
0,189 |
0,441 |
0,343 |
Используя
формулу (2), найдем функцию распределения:
1.
если ![]() ,
то
,
то ![]() ;
2.
если
;
2.
если ![]() ,
то
,
то ![]() ;
3.
если
;
3.
если ![]() ,
то
,
то ![]() ;
4.
если
;
4.
если ![]() ,
то
,
то ![]() ;
5.
если
;
5.
если ![]() ,
то
,
то ![]() .
.
Итак, функция
распределения аналитически может быть
записана так:
![]() Теперь
построим график этой функции.
Теперь
построим график этой функции.
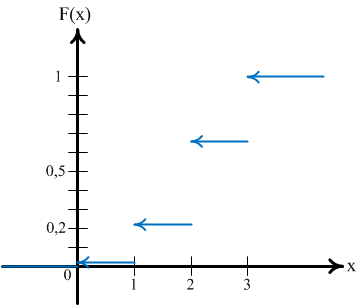
Рис.2
То есть
функция распределения для дискретной
случайной величины является
кусочно-постоянной функцией,
имеющей
конечное число точек разрыва 1-го
рода.
Функция распределения непрерывной
случайной величины является непрерывной
функцией.
Пример
7. Дана
функция распределения вероятностей
непрерывной случайной величины ![]() :
:
![]() Найти
Найти ![]() ,
построить график функции распределения,
вычислить вероятность того, что в
результате испытания
случайная
величина
,
построить график функции распределения,
вычислить вероятность того, что в
результате испытания
случайная
величина ![]() примет
значение в интервале (1;2).
Решение. Для
нахождения
примет
значение в интервале (1;2).
Решение. Для
нахождения ![]() воспользуемся
непрерывностью функции распределения:
воспользуемся
непрерывностью функции распределения:
![]() ,
поэтому
,
поэтому ![]() ,
следовательно
,
следовательно ![]() .
Построим
график функции распределения:
.
Построим
график функции распределения:
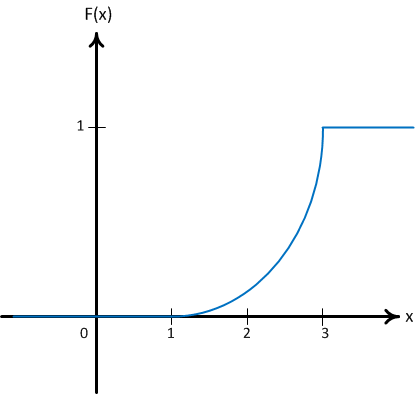
Рис.3
По формуле
(3) находим: ![]() .
.
Вопрос. Если
случайная величина ![]() принимает
значения, не большие 4, то
принимает
значения, не большие 4, то ![]() равно:
равно:
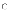 4
4
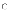 5
5
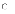 0
0
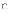 1
1
Плотность распределения вероятностей
Функция
распределения для непрерывной случайной
величины является ее исчерпывающей
вероятностной
характеристикой, но
она имеет недостаток, так как по ней
трудно судить о характере распределения
случайной
величины в небольшой
окрестности той или иной точки числовой
оси. Более наглядное представление
о
характере распределения непрерывной
случайной величины в окрестностях
различных точек дает функция,
которая
называется плотностью
распределения вероятностей и
обозначается ![]() .
.
![]() (4)
(4)
Плотность
распределения - это средняя вероятность,
которая приходится на единицу длины
промежутка ![]() .
Она
указывает на то, как часто случайная
величина
.
Она
указывает на то, как часто случайная
величина ![]() появляется
в некоторой окрестности точки
появляется
в некоторой окрестности точки ![]() при
повторении
испытаний. Эту функцию еще называют
дифференциальным законом распределения.
На
рис.4 дан примерный вид функции
при
повторении
испытаний. Эту функцию еще называют
дифференциальным законом распределения.
На
рис.4 дан примерный вид функции ![]() .
.
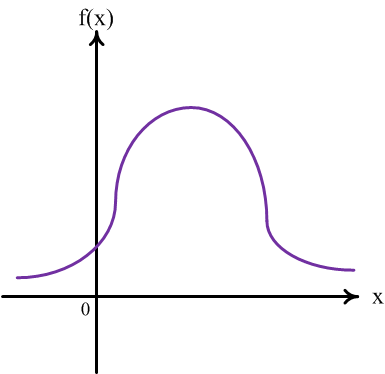
Рис.4
График
функции ![]() называется кривой
распределения.
Так
как
называется кривой
распределения.
Так
как ![]() ,
то
,
то
![]() (5)
(5)
Свойства плотности распределения
1. ![]() ;
2.
;
2. ![]() .
Геометрически
это означает, что площадь под кривой
распределения равна 1.
Функция
распределения и плотность распределения
связаны еще одним соотношением:
.
Геометрически
это означает, что площадь под кривой
распределения равна 1.
Функция
распределения и плотность распределения
связаны еще одним соотношением:
![]() (6)
(6)
Вероятность
того, что случайная величина ![]() примет
значение из промежутка
примет
значение из промежутка ![]() ,
можно
вычислить с помощью плотности
распределения по формуле:
,
можно
вычислить с помощью плотности
распределения по формуле:
![]() (7)
(7)
Геометрически
это означает, что вероятность того, что
непрерывная случайная величина примет
значение из
промежутка ![]() ,
равна площади криволинейной трапеции
с основанием
,
равна площади криволинейной трапеции
с основанием ![]() (рис.5).
(рис.5).
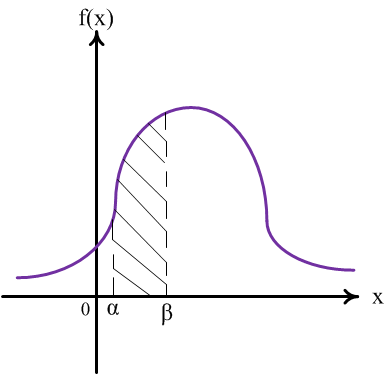
Рис.5
Пример
8. Дана
плотность распределения вероятностей
непрерывной случайной величины ![]() :
:
![]() Найти
Найти ![]() ,
построить график функции
,
построить график функции ![]() ,
найти
,
найти ![]() .
Решение. Для
нахождения коэффициента
.
Решение. Для
нахождения коэффициента ![]() воспользуемся
свойством 2 плотности распределения,
тогда
воспользуемся
свойством 2 плотности распределения,
тогда
![]() ,
получаем, что
,
получаем, что ![]() ,
следовательно,
,
следовательно, ![]() .
Теперь
построим график плотности распределения:
.
Теперь
построим график плотности распределения:
Рис.6
Требуемую
вероятность вычисляем по формуле
(7):
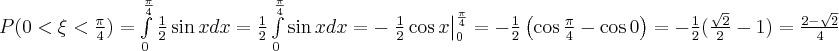 .
Вопрос. Для
каких случайных величин закон распределения
задается с помощью плотности распределения?
.
Вопрос. Для
каких случайных величин закон распределения
задается с помощью плотности распределения?
Ваш ответ

