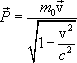Физика

Для выполнения тождества необходимо приравнять коэффициенты при х²,t²и хt. Раскрыв скобки и проведя соответствующие преобразования получим:

Из этих трех уравнений находим неизвестные величины ,  и ,:

При этом всюду мы выбрали положительный знак корня. Подставляя значения ,  и  в преобразования координат (6.3) и (6.4) находим:

(6.5)

Эти формулы носят название преобразований Лоренца. Формулы обратного преобразования от штрихованных к не штрихованным величинам:

(6.6)

Преобразования Лоренца приводят к выводам, коренным образом противоречащим привычным представлениям о свойствах времени и пространства, сложившимся на основе повседневного опыта. Рассмотрим несколько примеров применения преобразований Лоренца.

Пусть в системе K в точках с координатами и  происходят одновременно два события в момент времени . Согласно преобразованиям Лоренца в системе K’ этим событиям будут соответствовать координаты

и моменты времени

где 

Из написанных формул видно, что в случае, если события в системе K происходят в одном и том же месте пространства , то они будут совпадать в пространстве  и во времени  также в системе K’.

Если же события в системе K пространственно разобщены , то системе  они также окажутся пространственно разобщенными , но будут одновременными. Знак разности определяется знаком выражения . Из этого следует, что в разных системах , (при разных v) разность  будет различна по величине и может отличаться по знаку. Это означает, что в одних системах событие 1 будет предшествовать событию 2, в других системах, наоборот, событие 2 будет предшествовать событию 1. Сказанное относится только к событиям, между которыми отсутствует причинная связь.

Причинно связанные события (например, выстрел и попадание пули в мишень) ни в одной системе отсчета не будут одновременными и во всех системах событие, являющееся причиной, будет предшествовать следствию.

Рассмотрим стержень, расположенный вдоль оси х и покоящийся относительно системы K’ . Длина его в этой системе равна: , где  и - не изменяющиеся со временем  координаты концов стержня. Относительно системы K стержень движется со скоростью v. Для определения его длины в этой системе нужно отметить координаты концов стержня  и  в один и тот же момент времени . Их разность  даст длину стержня, измеренную в системе K. Чтобы найти соотношение между  и, следует взять ту из формул преобразования Лоренца, которая содержит , т.е.

откуда

или, окончательно

Таким образом, длина стержня , измеренная в системе относительно которой он движется, оказывается меньше длины , измеренной в системе, относительно которой он покоится. Это явление называется лоренцевым сокращением.

Скорости, при которых сокращение размеров движущихся материальных

тел становится заметным, носят название релятивистских скоростей, и в настоящее время они достигнуты в крупных масштабах в лабораторной практике и в новых промышленных аппаратах. В ядерных реакторах атомныхэлектростанций быстрые нейтроны движутся со скоростями, для которых , т.е. сокращение длины порядка 0,3%. Релятивистские частицы, приходящих на Землю космических лучей имеют  и продольные размеры сокращаются в 10 миллионов раз. Для быстро летящих заряженных частиц подобной продольной деформации подвергается сопровождающее их электромагнитное поле. На рис.6.За изображены линии поля и постоянного потенциала электрического поля точечного заряда, когда он неподвижен. На рис. 6.36 тот же заряд, движущийся с не слишком большой скоростью, на рис.6.3в - со скоростью, очень близкой скорости света. Если в первом случае поле сферически симметрично, то в последнем оно практически сжимается в «лепешку», перпендикулярную к направлению движения. Эту деформацию электромагнитного поля можно обнаружить на опыте. Релятивистская частица будет взаимодействовать с неподвижным пробным зарядом , помещенным на ее пути, лишь в течении очень краткого времени, когда «лепешка» силовых линий проходит через заряд .

Любопытно, что визуально (или на фотографии) изменение формы тела даже при сравнимых со скоростью света скоростях, не может быть обнаружено. Причина этого весьма проста. Наблюдая визуально или фотографируя какое-либо тело, мы регистрируем импульсы света от разных участков тела достигшие одновременно сетчатки глаза или фотопластинки. Испускаются же эти импульсы не одновременно. Импульсы от более удаленных участков тела были испущены раньше, чем от более близких участков. Таким образом, если тело движется, на сетчатке глаза получается искаженное изображение тела. Соответствующий расчет показывает, что следствием искажения будет уничтожение лоренцевого сокращения, так что тела кажутся не искаженными, а лишь повернутыми. Если бы лоренцевого сокращения не было, тела казались бы вытянутыми в направлении движения.

Пусть в точке х’, неподвижной относительно системы K’, происходит событие длящееся время .Началу события соответствует в этой системе координата и момент времени, концу события - координата и момент времени . Относительно системы K точка, в которой происходит событие, перемещается. Согласно преобразованиям Лоренца началу и концу события соответствуют в системе K’.

Откуда

или

Время , отсчитанное по часам, движущимся вместе с телом, называют собственным временем этого тела. Kак видно из уравнения, собственное время всегда меньше, чем время, отсчитанное по часам, движущимся относительно тела.Релятивистский эффект замедления хода времени позволяет в принципе осуществить «путешествие в будущее» (но не в прошлое). В самом деле, пусть космический корабль, движущийся со скоростью  (где ) относительно Земли, совершает перелет от Земли до некоторой звезды и обратно. Если свет проходит путь  от звезды до Земли за время , то  и для земного наблюдателя продолжительность перелета равна:

Именно настолько постареют люди на Земле к моменту возвращения космонавтов. С другой стороны, по часам, установленным на космическом корабле, полет займет меньшее время , которое:

В соответствии с принципом относительности все процессы на космическом корабле (в том числе и процесс старения космонавтов) идут так же, как и на Земле, но не по земным часам, а по часам, установленным на корабле. Пусть, например, = 500 лет и  = 0,9999. Тогда

 лет, а  лет.

Пусть в системе отсчета K’ материальная точка движется вдоль оси х’ спостоянной скоростью Система K’ движется относительно системы K в том же направлении со скоростью v , Определим, чему равна скорость материальной точки v_o, относительно системы K, т.е. чему равно . Пусть при  м.т. находится в начале координат, причем . Для системы K:

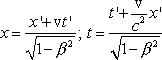
Подставляя и t в формулу для v_o

Делим числитель и знаменатель на t

Это равенство выражает собой релятивистский закон сложения скоростей. При малых значениях скоростей и  имеем

т.е. релятивистский закон сложения скоростей переходит в классический

Уравнения классической механики инвариантны по отношению к преобразованиям Галилея, по отношению же к преобразованиям Лоренца они оказываются неинвариантными. Из теории относительности следует, что уравнение динамики, инвариантное по отношению к преобразованиям Лоренца, имеет вид:

где - инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы, - сила действующая на частицу. Сопоставим с классическим уравнением

Мы приходим к выводу, что релятивистский импульс частицы равен

(6.7)

Релятивистская масса.

Определив массу частицы m как коэффициент пропорциональности между скоростью и импульсом, получим, что масса частицы зависит от ее скорости.

(6.8)

Энергия в релятивистской динамике.

Для энергии частицы в теории относительности получается выражение:

(6.9)

Из (2.3) следует, что покоящаяся частица обладает энергией

(6.10)

Эта величина носит название энергии покоя частицы. Kинетическая энергия, очевидно, равна

(6.11)

Приняв во внимание, что , выражение для полной энергии частицы можно написать в виде

(6.12)

Из последнего выражения вытекает, что энергия и масса тела всегда пропорциональны друг другу. Всякое изменение энергии тела  сопровождается изменением массы тела

и, наоборот, всякое изменение массы  сопровождается изменениемэнергии . Это утверждение носит название закона взаимосвязи или закона пропорциональности массы и энергии.

В механике не рассматривается изменение внутреннего состояния тел. Для механики, которая решает задачи о движении тела как целого, это не имеет значения. Мы говорим, что при движении часть механической энергии перешла, например, в тепловую и все. Какие процессы сопровождают переход механической энергии в тепло не уточняется.

Термодинамика и молекулярно – кинетическая теория (м.к.т.) изучают внутреннее строение и состояние тел, которые могут меняться в таких процессах, как нагревание и охлаждение, тепловое расширение и сжатие, фазовые превращения, диффузия, теплопроводность и вязкость и т.д.

Термодинамика и молекулярно – кинетическая теория, имея общий предмет изучения, различаются по методу исследований явлений. Термодинамика опирается на небольшое число фундаментальных законов, справедливых всегда и для всех макроскопических тел. Сведения о конкретном виде тел (например о данном газе, жидкости или твердом теле) термодинамика берет из опыта (обычно в виде так называемого уравнения состояния или зависимости физических величин от температуры или давления). При этом молекулярное строение тел остается за рамками термодинамического исследования.

Молекулярно – кинетическая теория, напротив, для каждого конкретного тела создает модель его молекулярного состояния и из этой модели методами математической статистики (ввиду большого числа молекул) выводит конкретные свойства данного вещества. Методы термодинамики и м.к.т. взаимно дополняют друг друга.

Термодинамическое состояние тела (например, газа) характеризуется его массой  , молярной массой μ, давлением  , объемом  , температурой  (а возможно, и другими величинами, например, определяющими его химический состав). Все эти величины называются термодинамическими параметрами тела. Однако, как будет видно из дальнейшего, такие параметры, как  ,имеют смысл только тогда, когда тело находится, хотя бы приближенно, в так называемом состоянии термодинамического равновесия (т.д.р.). Так называется состояние, в котором все термодинамические параметры остаются со временем постоянными (к этому следует добавить еще условие отсутствия стационарных потоков). Если, например, быстро подогревать газ, как это показано на рис. 9.1, температура непосредственно подогреваемой части сосуда А окажется выше температуры части В. Не будут равны и давления в частях А и В. В этом случае не имеет смысла понятие температуры  или давления  всего газа. Другой пример – впустим в газ пучок быстрых молекул. Ясно, что не имеет смысла говорить о температуре газа до тех пор, пока быстрые молекулы, вследствие ряда столкновений с другими, не приобретут скоростей порядка средней скорости остальных молекул, иначе говоря, пока система не придет в состояние т.д.р.

В состоянии т.д.р. для каждого вещества термодинамические параметры связаны между собой так называемым уравнением состояния:

(9.1)

Таким уравнением состояния для идеального газа является уравнение Менделеева – Клапейрона:

(9.2)

Здесь R=8,31 Дж/(мольК) – универсальная газовая постоянная, μ - молярная масса. Для углерода (С) величина μ составляет 12г, для водорода (H₂) – 2г, для кислорода (О₂) – 32г, для воды (Н₂О) – 18г и т.д.

В моле любого вещества содержится одно и то же количество молекул N₀, называемое числом Авогадро:

(9.3)

Это объясняется тем, что значение моля любого вещества выбрано пропорциональным массе молекулы этого вещества. Масса молекулы может быть получена делением массы моля на число Авогадро:

(9.4)

Отношение универсальной газовой постоянной R к числу Авогадро (т.е. универсальная газовая постоянная, приходящаяся на одну молекулу) называется постоянной Больцмана:

(9.5)

В формулу (9.2) входят еще давление, объем, температура и масса газа. Давление Р в системе СИ измеряется в ньютонах на квадратный метр или паскалях (Н/м²=Па), объем V – в кубических метрах (м²), масса m – в килограммах (кг), температура T – в кельвинах (К). Абсолютная температура Т отсчитывается от абсолютного нуля (-273,15°С), т.е. Т=t+273,15, где t – температура по Цельсию.

Если количество вещества равно 1 молю, то (9.2) превращается в

(9.6)

Идеальным газом называется газ, настолько разреженный, что он подчиняется уравнению (9.2) или(9.6). Смысл этого определения состоит, очевидно, в том, что для подчинения уравнению (9.6) газ должен быть достаточно разреженным. Если газ, напротив, сжат до достаточно больших плотностей (так называемый реальный газ), то вместо (9.6) имеем

(9.7)

Это – уравнение состояния реального газа или уравнение Ван-дер-Ваальса. Здесь a и b – постоянные.

Под внутренней энергией (U) понимается вся энергия системы (тела) за исключением механической энергии системы как целого. Что именно входит во внутреннюю энергию системы? Сюда входит кинетическая энергия поступательного движения ее молекул, потенциальная энергия их взаимодействия между собой, энергия возбуждения колебаний и вращений молекул. Здесь перечислены лишь те виды энергии системы, которые могут меняться в рассматриваемых нами термодинамических процессах. Например, энергию возбуждения атомных ядер нужно будет включить, если будут рассматриваться температуры, при которых такое возбуждение может произойти.

Поскольку состояние термодинамической системы (например, газа) определяется величинами m, μ, V, T (давление P само определяется этими же величинами), то от них должна зависеть и внутренняя энергия U. Опустим пока постоянные для данного тела m и μ (ниже примем их во внимание), запишем U=U(V,T). Зависимость внутренней энергии от объема V связана с тем, что при изменении объема меняется расстояние между молекулами и, следовательно, потенциальная энергия их взаимодействия. Эта зависимость существенна только для реального газа. Для идеального газа внутренняя энергия должна зависеть только от температуры, т.е. U=U(T), так как температура определяет среднюю кинетическую энергию молекул.

Рассмотрим газ, находящийся в цилиндре с поршнем, позволяющем менять объем газа (рис 9.2). Отметим, что слово «газ» здесь совершенно условно. Это может быть жидкость, кристалл и вообще любое тело. Цилиндр контактирует с нагревателем или холодильником, который может сообщать газу тепло или отбирать его.

Пусть на поршень оказывается внешнее давление, величина которого может быть любой.

Все процессы, которые будем рассматривать ниже, будут квазистатическими, т.е. медленными настолько, чтобы можно было считать, что в каждый момент газ находится в состоянии т.д.р. Если очень быстро сжать газ, то давление его у поршня окажется на какой-то момент больше, чем в стальном объеме, и тогда нельзя будет говорить о давлении газа вообще. Такой процесс не является квазистатическим. Приближенно квазистатическими являются и процессы, достаточно быстрые с технической точки зрения, например процессы, происходящих в цилиндрах двигателя автомашины во время работы мотора (оказывается, для приближенной квазистатичности требуется, чтобы скорость поршня была мала по сравнению со скоростью звука в газе).

Работа над газом выполняется внешними силами при его сжатии. Работа самого газа выполняется при его расширении. Пусть газ расширяется так, что поршень на рис.9.2 поднимается на величину dx. Тогда газ выполнит работу  (S – площадь поршня). Получим