2. Частные случаи расположения плоскости в пространстве

Рассмотрим общее уравнение плоскости в пространстве:

.

1). Если , то общее уравнение примет вид

,

координаты точки удовлетворяют этому уравнению, значит плоскость проходит через начало координат.

2). Если , то уравнение будет иметь вид

,

тогда вектор нормали к плоскости будет перпендикулярен оси, значит данная плоскость параллельна оси.

3). Аналогично, для плоскость будет параллельна оси.

4). Для плоскость будет параллельна оси.

5). Если , то уравнение плоскости примет вид, то есть плоскость проходит через начало координат и параллельна оси, значит плоскость проходит через ось.

6). Если , то плоскость проходит через ось.

7). Если , то плоскость проходит через ось.

8). Если , то уравнение плоскости будет иметь вид , вектор нормали к плоскостиперпендикулярен плоскости, следовательно, данная плоскость будет параллельна плоскости.

9). Если , то плоскость параллельна плоскости.

10). Если , то плоскость параллельна плоскости.

11). Если , то уравнение плоскостиили, эта плоскость проходит через начало координат и параллельна плоскости, то есть это координатная плоскость.

12). Если , то есть-это уравнение координатной плоскости.

13). Если , то есть- это уравнение координатной плоскости.

3. Различные уравнения плоскости в пространстве

Рассмотрим общее уравнение плоскости в пространстве:

. (3.1)

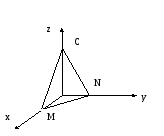
Пусть плоскость не параллельна ни одной из осей, тогда эта плоскость отсекает на осях координат отрезки (см. рис).

Воспользуемся общим уравнением (3.1) плоскости, где

.

Найдем коэффициенты уравнения, используя координаты точек пересечения плоскости с осями координат. Так как эти точки лежат в плоскости, то их координаты удовлетворяют уравнению, следовательно,, откуда,

, тогда и, тогда. Подставляя эти соотношения в (3.1), получим, так как, разделим это равенство наи получим

. (3.2)

Это уравнение плоскости в отрезках на координатных осях, числа показывают, какие отрезки на осях координат отсекает данная плоскость.

Пусть известны координаты вектора нормали к плоскости и координаты точки, которая принадлежит плоскости. Надо составить уравнение данной плоскости.

Возьмем произвольную точку плоскости , тогда вектортоже будет принадлежать плоскости, вектор нормали, перпендикулярный плоскости, перпендикулярен любому вектору, лежащему в этой плоскости, то есть, а тогда скалярное произведение этих векторов равно нулю

(3.3)

Получили уравнение плоскости, проходящей через заданную точку с заданным вектором нормали. При всевозможных значениях равенство (3.3) определяет совокупность всех плоскостей, проходящих через точку, и называется уравнением связки плоскостей, проходящих через заданную точку.

Пример 1. Даны точки . Составить уравнение плоскости, проходящей через точкуи перпендикулярной вектору.

Решение. Вектор будет являться вектором нормали плоскости, его координаты равны. Теперь воспользуемся уравнением (3.3):

или

Пусть заданы три точки . Надо составить уравнение плоскости, проходящей через заданные точки. Для этого возьмем произвольную точкуэтой плоскости, тогда векторылежат в данной плоскости, то есть компланарны. Следовательно, их смешанное произведение равно нулю, или

(3.4)

Уравнение (3.4) – уравнение плоскости, проходящей через три заданные точки.