
- •Практикум. Квадратичные формы
- •Понятие квадратичной формы. Преобразования квадратичных форм
- •2. Приведение квадратичных форм к каноническому виду методом Лагранжа
- •3. Ортогональные преобразования. Приведение квадратичной формы к каноническому виду методом ортогональных преобразований
- •4. Закон инерции квадратичной формы. Критерий Сильвестра
- •Знакоопределенные и знакопеременные квадратичные формы
- •Критерий Сильвестра
Критерий Сильвестра
Тип квадратичной формы можно определить, не приводя ее к каноническому виду. Следующий ниже критерий Сильвестра позволяет определить тип квадратичной формы по знакам угловых миноров ее матрицы.
Рассмотрим
угловые миноры
![]() (
(![]() ),
являющиеся определителями подматриц
),
являющиеся определителями подматриц
![]() матрицы
матрицы
![]() квадратичной формы:
квадратичной формы:
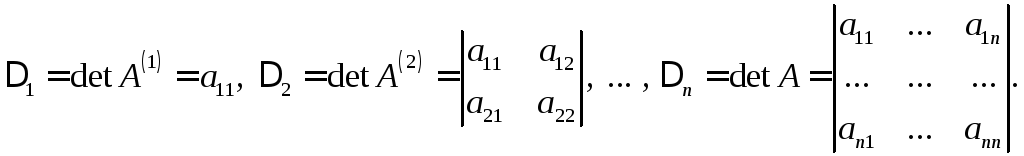
Теорема 6 (критерий
Сильвестра знакоопределенности
квадратичной формы).
Квадратичная
форма
![]() является:
является:
1) положительно
определенной тогда и только тогда, когда
все угловые миноры
![]() матрицы
матрицы![]() положительны:
положительны:
![]() (
(![]() )
)
2) отрицательно
определенной тогда и только тогда, когда
все угловые миноры
![]() матрицы
матрицы![]() отличны от нуля и их знаки чередуются,
начиная со знака минус:
отличны от нуля и их знаки чередуются,
начиная со знака минус:
![]()
В заключение приведем таблицу оценки знакоопределенности квадратичных форм по двум основным критериям.
|
Квадратичная форма |
Обозна- чение |
Оценка знакоопределенности формы | |
|
по главным минорам матрицы квадратичной формы |
по собственным значениям матрицы квадратичной формы | ||
|
положительно определенная |
|
если все угловые
миноры
|
если все собственные значения положительны |
|
отрицательно определенная |
|
если все угловые
миноры
|
если все собственные значения отрицательны |
|
неотрицательно определенная |
|
если все угловые
миноры
|
если все собственные значения неотрицательны |
|
неположительно определенная |
|
если в угловых
минорах
|
если все собственные значения неположительны |
|
знакопеременная |
|
|
среди собственных значений имеются как положительные, так и отрицательные |
Пример 6. Исследовать на знакоопределенность следующие квадратичные формы от двух переменных
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Решение.
1) Матрица формы
![]() имеет вид
имеет вид
 .
.
Ее угловые миноры равны
![]() ,
,
 .
.
Согласно критерию
Сильвестра, так как все угловые миноры
положительны, квадратичная форма
![]() являетсяположительно
определенной.
являетсяположительно
определенной.
2) Матрица формы
![]() имеет вид
имеет вид
 .
.
Ее угловые миноры равны
![]() ,
,
 .
.
Согласно критерию
Сильвестра, так как все угловые миноры
матрицы
отличны от нуля и их знаки чередуются,
начиная со знака минус,
то квадратичная форма
![]() являетсяотрицательно
определенной.
являетсяотрицательно
определенной.
3) Матрица формы
![]() имеет вид
имеет вид
 .
.
Ее угловые миноры равны
![]() ,
,
 .
.
Так как в этом
случае второй угловой минор отрицателен,
то согласно таблице квадратичная форма
![]() являетсязнакопеременной.
являетсязнакопеременной.
4) Матрица формы
![]() имеет вид
имеет вид
 .
.
Ее угловые миноры равны
![]() ,
,
 .
.
Так первый угловой
минор положителен, а второй угловой
минор равен нулю, то согласно таблице
квадратичная форма
![]() являетсянеотрицательно
определенной.
являетсянеотрицательно
определенной.
Заметим, что в данном случае
![]() .
.
Пример 7. Исследовать на знакоопределенность квадратичную форму от трех переменных
![]() .
.
Решение. Матрица формы имеет вид
 .
.
Ее угловые миноры положительны:
![]() ,
,
 ,
, .
.
Согласно критерию Сильвестра, так как все угловые миноры положительны, то квадратичная форма является положительно определенной.
Практикум №3. Квадратичные формы
