Работа № 3

ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ

1. Цель и содержание работы

Изучение численных методов дифференцирования и интегрирования и приобретение навыков в составлении программ, реализующих эти методы.

2. Численное дифференцирование

Необходимость в численном дифференцировании возникает в тех случаях, когда дана таблица значений функции, а ее представление в аналитическом виде неизвестно. Чем более плавный вид имеет кривая, проходящая через табличные точки, тем более близкие к реальным результаты дает численное дифференцирование.

Для вычисления значения производной функции y=f(x) используют приближенное равенство Это соотношение называется аппроксимацией (приближением) производной с помощью отношения конечных разностей. Для таблично заданной функции, в случае постоянного шага – разности между соседними значениями аргумента – получим формулы вычисления производной в точке x=x₁ в зависимости от способа вычисления конечных разностей.

С помощью левых разностей: , , (1)

С помощью правых разностей: , , (2)

С помощью центральных разностей: , . (3)

Старшие производные отыскиваются аналогичным способом, например

(4)

Для хорошей аппроксимации производной нужно использовать значения функции во многих узлах. Погрешность численного дифференцирования имеет несколко составляющих. Одна из них – погрешность аппроксимации или погрешность усечения. Она определяктся величиной остаточного члена в разложении функции в ряд Тейлора. Погрешность аппроксимации при уменьшении шага h, как правило уменьшается.

Другая составляющая – погрешность, вызванная неточными значениями функции в узлах, а также погрешность округления при проведении расчетов на ЭВМ. Погрешность округления возрастает с уменьшением шага h. Поэтому суммарная погрешность численного дифференцирования может убывать при уменьшении шага лишь до некоторого предельного значения, после чего дальнейшее уменьшение шага не повысит точности расчетов.

Численное дифференцирование можно выполнить, заменяя функцию y(x) интерполяционным полиномом, производные которого можно найти аналитически с помощью соответствующих формул.

Если функция аппроксимирована интерполяционным многочленом Ньютона (см. лаб. №3, разд.7):

Дифференцируя этот многочлен по переменной x с учетом правила дифференцирования сложной функции: можно получить формулы для вычисления производных любого порядка:

При аппроксимировании функции интерполяционным многочленом Лагранжа с равномерным расположением узлов ( (см. лаб №3, разд.6) найдем производные для случая трех узлов интерполяции (n=2):

С помощью интерполяционных многочленов Лагранжа можно получить аппроксимации для старших производных. В случае трех узлов интерполяции (n=2) для второй производной имеем

3. Задание для лабораторной работы по методам численного дифференцирования

Провести расчет крутизны передаточной вольт-амперных характеристик мощного полевого транзистора методом численного дифференцирования, указанным преподавателем.

Задание. Характеристика транзистора задана таблицей. Значения токов приведены в амперах.

				Напряжение на стоке, В
Напряжение на затворе, В	0	10	20		30	40	50
3	0	0	0		0	0	0
4	0	0,35	0,4		0,45	0,5	0,56
5	0	0,8	1,1		1,2	1,22	1.25
6	0	1,25	1,8		2	2,12	2,15
7	0	1,8	2,7		3,15	3,17	3,2
8	0	2,95	4		4,45	4,5	4,7

4. Численное интегрирование

М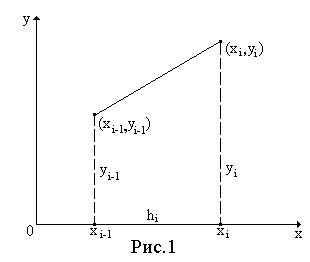етод прямоугольников. Простейшим методом численного интегрирования является метод прямоугольников. Он непосредственно использует замену определенного интеграла интегральной суммой: Обозначая (рис.1) получаем следующие формулы:

а) - левые границы элементарных отрезков

б) - правые границы элементарных отрезков

Более точным является вид формулы прямоугольников, использующий значения функции в средних точках элементарных отрезков (в полуцелых узлах):

Этот метод называют ещё методом средних.

Метод трапеций. Метод использует линейную интерполяцию, т.е. график функции y=f(x) представляется в виде ломаной, соединяющей точки Площадь всей фигуры (криволинейной трапеции) складывается из площадей элементарных прямолинейных трапеций (рис.1). Формула трапеций для численного интегрирования:

.

П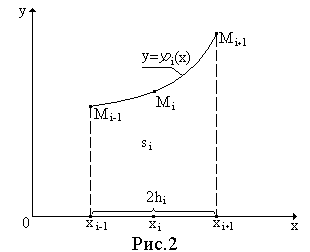огрешность численного интегрирования определяется шагом разбиения. Уменьшая его, можно добиться большей точности. Повышение точности можно также добиться повышением степени используемых интерполяционных многочленов.

Метод Симпсона. Разобьем отрезок интегрирования [a,b] на четное число n равных частей с шагом h. На каждом отрезке заменим подынтегральную функцию f(x) интерполяционным многочленом второй степени: . Коэффициенты этих квадратных трехчленов могут быть найдены из условий равенства многочлена в точках x_i соответствующим табличным данным y_i. В качестве можно принять интерполяционный многочлен Лагранжа второй степени, проходящий через точки

Элементарная площадь (рис.2) может быть вычислена с помощью определенного интеграла. Учитывая равенства получаем

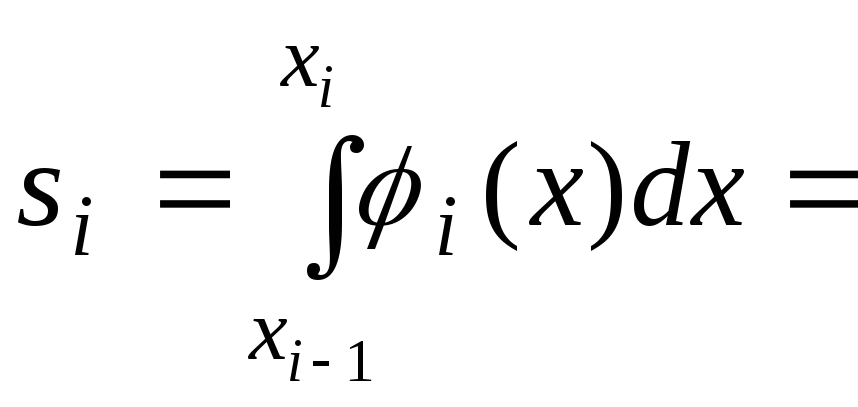
Просуммировав для всех элементарных отрезков, получим выражение (5), которое называется формулой Симпсона.

Погрешность метода Симпсона имеет порядок О(h³) и большинство функций при интегрировании этим методом дают самую малую погрешность. При уменьшении шага интегрирования h ошибка вычисления интеграла уменьшается. Однако в процессе практических вычислений при последовательном удвоении числа отрезков разбиения начинает сильно прогрессировать удельный вес ошибки округления, значение которой с некоторого момента ставит предел достижимой точности результата интегрирования.

(5)

Метод Монте-Карло. В практических приложениях часто приходится вычислять значение кратных интегралов. Кратный интеграл вычисляется для функции многих переменных по замкнутой ограниченной многомерной области. Вычислительная схема при этом в основном сохраняется: интервал, соответствующий изменению каждой переменной внутри области интегрирования, разбивается на фиксированное число отрезков. Таким образом, задается разбиение области интегрирования на определенное число элементарных многомерных объемов. Понятно, что при увеличении кратности интегралов число слагаемых очень быстро возрастает. В таких ситуациях предпочтительнее использовать для получения значения интеграла метод Монте-Карло.

В основе оценки искомого значения интеграла I лежит известное соотношение: I=y_ср, (6)

где y_ср - значение подынтегральной функции в некоторой «средней» точке области интегрирования, а  - (многомерный) объём области интегрирования. Предполагается, что подынтегральная функция F непрерывна в области интегрирования. Выберем в этой области n случайных точек M_i. При достаточно большом n приближенно можно считать:

Точность оценки значения интеграла методом Монте-Карло пропорциональна корню квадратному из числа случайных испытаний и не зависит от кратности интеграла. Именно поэтому применение метода целесообразно для вычисления интегралов высокой кратности.

Рассмотрим метод для простейшего случая интеграла:

В этой ситуации =b-a и равенство (6) принимает вид:

где - случайные точки, лежащие в интервале [a;b]. Для получения таких точек на основе последовательности случайных точек равномерно распределенных в интервале [0;1], достаточно выполнить преобразование:

5. Задание для лабораторной работы по методам численного интегрирования

Задание. Определить полный заряд ионизированной электронной плазмы с плотностью заряда Кл/м³ в объёме радиусом r=10 см.

Примечание. Элемент объёма сферы равен . Использовать метод численного интегрирования, указанный преподавателем.

Контрольные вопросы

1. В чём особенность задачи численного дифференцирования?

2. Как влияет на точность численного дифференцирования и интегрирования величина шага h ?

3. Можно ли добиться неограниченного уменьшения погрешности интегрирования и дифференцирования путем последовательного уменьшения шага?

Содержание отчета

1. Блок схема программы

2. Текст программы.

3. Результаты расчетов.

4. Выводы.

Библиографический список

1. Г.Корн, Т. Корн Справочник по математике (для научных работников и инженеров). М.: Наука, 1974. С.695-701.

2. Численные методы: Учебное пособие/В.М. Заварыкин, В.Г. Житомирский,М.П. Лапчик. М.: Просвещение, 1990. С.98-118.

3. Турчак Л.И. Основы численных методов: Учебное пособие. М.: Наука, 1987. С.78-113.

4. Вычислительные методы. Том 1/В.И. Крылов, В.В. Бобков, П.И. Монастырный.М.: Наука, !977. С.223-302.

5. Бахвалов Н.С. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). М.:Наука, 1975. С.95-201.