Работа № 5

ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ РАЗНОСТНЫМ МЕТОДОМ

1. Цель и содержание работы

Изучение разностных методов решения обыкновенных дифференциальных уравнений, приобретение навыков в составлении программ численного решения на примере задач электронной техники.

2. Теоретическая часть

Простейшим обыкновенным дифференциальным уравнением называется уравнение первого порядка . Основная задача, связанная с этим уравнением, известна как задача Коши: найти решение уравнения в виде функцииy=y(x), удовлетворяющую начальному условию.

Если начальное условие дифференциального уравнения задано, то решение единственно и получают его в виде таблицы значений искомой функции, воспользовавшись одним из методов интегрирования дифференциального уравнения. В результате вычислений на ЭВМ получают значения функции лишь на дискретном множестве значений x. Для анализа полученного решения воспользуемся разложением Фурье по модам. Если функция удовлетворяет условиям Дирихле, то ее в пределах области Х можно разложить в бесконечный ряд Фурье: где

Коэффициенты g_k определяют амплитуду мод с длиной волны X/k. Рассмотрим случай равномерной дискретной сетки, когда ее элементы x_j имеют постоянный шаг h и число всех точек функции равно N. В этом случае значение функции в узле j можно записать в виде ряда Фурье, содержащего конечное число членов ,где амплитуда моды дается формулой .В случае дискретной аппроксимации число мод конечно, это вызвано тем, что мы пренебрегаем фурье-модами функции, длина которых меньше h.

Рассмотрим разностную аппроксимацию производных. Аппроксимация второго порядка имеет вид где

Произведем сравнение между точной и разностной производной для одной из мод Фурье: . (1)

Так как то (2)

Для малых значений kh величина sin(kh)kh, поэтому формулу (2) можно представить формулой (1). Аппроксимация второй производной на разностной сетке имеет вид Тогда в результате аналогичных преобразований получим ,В случае малой величины kh

Таким образом, конечно-разностное отношение является хорошей аппроксимацией первой и второй производной, если мало волновое число k и соответственно велика длина волны 2/k. Чем длиннее волна, тем аппроксимация лучше.

При решении физических задач предпочтение обычно отдается простейшим разностным схемам. Они неявным образом содержат в себе те или иные законы сохранения, что очень важно для численного моделирования физических процессов. Их часто называют консервативными методами. Кроме того, они позволяют за конечное число шагов достаточно быстро получить решение.

3. Разностные схемы для обыкновенных дифференциальных уравнений

Рассмотрим разностные схемы и критерии устойчивости для дифференциального уравнения с начальными условиями где L в общем случае некоторый линейный оператор, погрешность на n–м шаге обозначим как ⁿ , а на (n+1)-м - ⁿ⁺¹ . Тогда Чтобы численный метод был устойчив, необходимо или |g|1.

Метод Эйлера первого порядка имеет вид (3)

Найдем условие его устойчивости: . (4)

Предположив, что ⁿ мало, разложим функцию f(u)=f(uⁿ +ⁿ) в ряд Тейлора в окрестности uⁿ: . (5)

Так как основное уравнение имеет вид (3), то вычитая из (4) уравнение (3) и учитывая (5), имеем из которого следует простое выражение для множителя переходаДля устойчивости метода необходимо выполнение условия что вытекает из условия |g|1. Решением (5) является система неравенств: (6)

Для >0 система неравенств (6) принимает вид , .

Если известен вид функции f(u,t), то легко вычислить временной шаг, при котором численная схема будет устойчива.

Наиболее распространенные разностные схемы для решения дифференциальных уравнений приведены в таблице. Особое место среди разностных методов, приведенных в таблице, занимает неявный метод. Он является устойчивым при любых значениях .

Метод Адамса-Бошфорта является методом, сглаживающим функцию, так как используется значение функции на (n+1)-м временном слое. Но шаг у него вдвое меньше обычного. Для своей реализации он требует больший объем памяти.

Простая схема Эйлера очень удобна для реализации на ЭВМ, но имеет первый порядок точности по . Две разновидности двухшагового метода есть не что иное, как модифицированные схемы Эйлера. Обычно предпочтение отдается первой схеме, поскольку она проще в реализации.

Вопрос о получении требуемой точности решения дифференциального уравнения является сложным, поскольку априорную оценку погрешности получить тяжело. Поэтому основной является апостериорная оценка точности, для получения которой проводят расчет на двух или более сгущающихся сетках и применяют правило Рунге или Рунге-Ромберга. Сущность этого метода заключается в следующем.

Пусть (t) – производная, которая подлежит аппроксимации; f(t,h) –конечно-разностная аппроксимация этой производной на равномерной сетке с шагом h; R – погрешность (остаточный член) аппроксимации, главный член которой можно записать в виде т.е.Тогда выражение для аппроксимации производной в общем случае можно представить в виде(7)

Запишем это соотношение в той же точке t при другом шаге h₁=kh. Получим

(8)

Приравнивая правые части (7) и (8), находим выражение для главного члена погрешности аппроксимации производной:

Подставляя найденное выражение в равенство (7), получаем формулу Рунге:

(9)

Эта формула позволяет по результатам двух расчетов значений производной f(t,h) и f(t,kh) (с шагами h и kh) с порядком точности n найти ее уточненное значение с порядком n+1.

Мы рассмотрели уточнение решения, получаемого при двух значениях шага. Предположим теперь, что расчеты могут быть проведены с шагами h₁, h₂, …, h_q. Тогда можно получить уточненное решение для производной (t) по формуле Ромберга, которая имеет вид

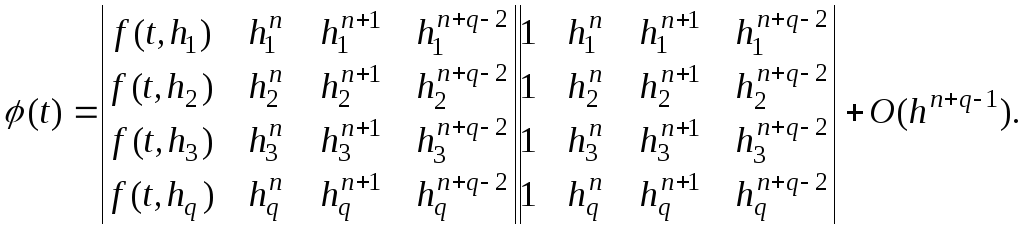
Таким образом, порядок точности возрастает на q-1. Для успешного применения уточнения исходная функция должна иметь непрерывные производные достаточно высокого порядка.

Разностными методами можно решать уравнения более высоких степеней, заменив уравнения высокого порядка несколькими уравнениями первого порядка. Например, в случае движения электрона в электрическом поле уравнение движения можно представить в виде системы двух уравнений

.

При решении задач математической физики часто используется метод Рунге-Кутта. Он является неконсервативным с точки зрения физических законов сохранения, но имеет высокий порядок точности. Трудно оценить шаг, при котором он устойчив. Однако он сходится при большем шаге, чем в схеме Эйлера. Сущность метода состоит в последовательном вычислении коэффициентов, посредством которых находится значение функции на следующем шаге. Наиболее часто на практике применяют метод Рунге-Кутта четвертого порядка:

,

(10)

А система двух дифференциальных уравнений : , интегрируется по схеме (11)

где

(12)

Метод Рунге-Кутта распространяется также и на уравнения более высокого порядка. Но для уравнения используется не традиционная схема, так как она требует большего объема памяти, а несколько преобразованная:

(13)

Схемы Рунге-Кутта имеют множество достоинств по сравнению с другими методами. Они обладают хорошей точностью и являются явными. Все схемы допускают расчет с переменным шагом.

Погрешности различных схем Рунге-Кутта, связанные с максимумами модулей соответствующих производных, определяются довольно сложными формулами, отчего на практике они никогда не используются.