3.Формулы включений и исключений.Характеристические функции мнежества.
Характеристическая функция подмножества — функция с областью значений {0, 1}, вычисляемая для любого элемента содержащего его множества, результатом которой является число, обозначающее принадлежность элемента подмножеству.
Если элемент множества принадлежит подмножеству, значение характеристической функции равно единице, если же нет — нулю.
Свойства:
1.
*
=
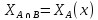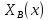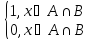
2.
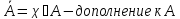
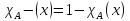
3.
.
+
-
*
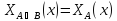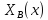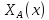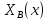
4.
5.
,
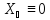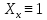
Комбинируя выписанные три формулы получим фориулу включений и исключений для m+1 свойств a1,a2,….,am,am+1.Что и требовалось доказать. □
4.Разбиения.Числа Стерлинга 1 и 2 рода. Свойства чисел Стерлинга. Числа Белла.
Под разбиением n-элементного множества A на k блоков будем понимать произвольное семейство π = {B1 ,…,Bk}, такое, что B1 U … U Bk = A, Bi ∩ Bj = Ø для 1≤i≤k. Подмножества B1,…,Bk будем называть блоками семейства π. Множество всех разбиений множества А на k блоков будем обозначать Пk(A), а множество всех разбиений через П(А).
Число Стирлинга второго рода S (n, k) есть число разбиений n-элементного множества на k блоков: S (n, k) = |Пk (A)|, где |А| = n.
Теорема 1
S (n, k) = S (n-1, k-1) + kS (n-1, k) для 0≤k≤n,
Доказательство. Пусть А={x1,х2,…,хn}. Количество разбиений, в которых есть блок из 1 элемента {xn} равно
S(n-1,k-1).Рассматриваем разбиения, в которых хn водит элементом в некоторый большой блок. Эти разбиения получаются из разбиений {x1,….,xn} на k блоков( их количество S(n-1,k) и добавлением элемента хn по очереди в каждый из k блоков. Общее количество равно kS(n-1,k).
Теорема 2
S
(n,
k)
=
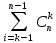S
(I,
k-1),
k≥2.
Доказательство:
Рассмотрим
множество всех разбиений множества А
= {1, …, n}.
Это множество распадается на различные
классы, соответствующие разным
подмножествам множества А, которые
являются блоками, содержащими элемент
n.
Для каждого b-элементного
подмножества B
A,
содержащего элемент n,
существует в точности S
(n-b,
k-1)
разбиений множества A
на k
блоков, содержащих B
в качестве блока. Действительно, каждое
такое разбиение однозначно соответствует
разбиению множества A\B
на k-1
блоков, b-элементное множество B
A,
содержащее элемент n,
можно выбрать
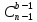способами. Следовательно,
S
(n,
k)
=
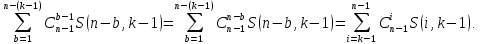
Числа
Стирлинга первого рода
s
(n,
k)
есть коэффициенты при последовательных
степенях переменной х в многочлене
[x]k:
[x]n
=
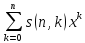Видно, чтоs(n,
k)
= 0 для k>n
Теорема 3
s (n, k) = s (n-1, k-1) – (n-1) s (n-1, k), для 0<k<n
s (n, n) = 1, для n≥0
s (n, 0) = 0, для n>0
Док-во:. Формулу получим, сравнивая коэффициенты при xk в обеих частях равенства.
[x]n = [x]n-1 (x-n+1)
Имеем
=
=
=
+
+
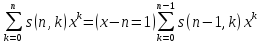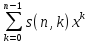s
(n-1
,n-1)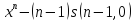
Св-ва чисел Стирлинга 1го рода:
1) s (0,0) = 1
2) s (n,k) = 0 k>n
3) s (n,k) = 1 n≥0
4) s (n,0) = 0, n>0
5) s (n,1) = (-1)n-1(n-1)!, n≥0
Числа
Белла Вn
= |П (A)|,
где |A|
= n. Другими словами,
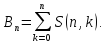
Теорема.
=
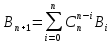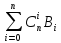
Доказательство.
Блок, содержащий элемент Xn+1
состоит из (n-i+1)
элементов. Кол-во разбиений оставшихся
I
элементов равно Bi.Блок
из n-iэлементов
можно выбрать из {x1,…,xn}
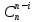способами.