- •1.Размещения, перестановки, сочетания
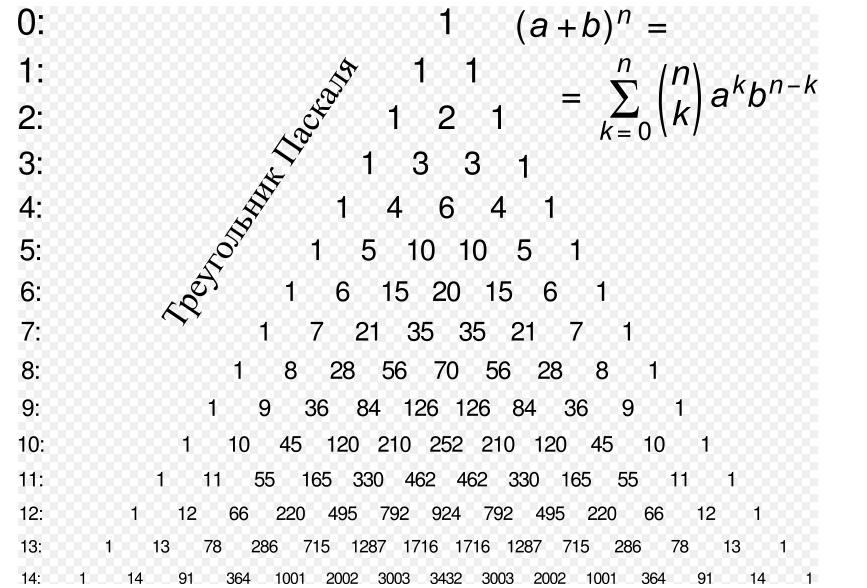
- •2.Бином Ньютона. Полиномиальная теорема.Свойства биномиальных коэффициентов. Треугольник Паскаля.
- •3.Формулы включений и исключений.Характеристические функции мнежества.
- •4.Разбиения.Числа Стерлинга 1 и 2 рода. Свойства чисел Стерлинга. Числа Белла.
- •5,6 Производящие функции, свойства
- •7. Линейные рекуррентные соотношения с постоянными коэффициентами. Теорема о решении линейных рекуррентных соотношений. Числа Фибоначчи.
- •8. Булев куб. Его элементы. Функции алгебры логики. Задание функций таблицами. Элементарные функции и их свойства. Фиктивные и существенные переменные.
- •9. Формулы. Представление функций формулами. Операция суперпозиции. Эквивалентность формул.
1.Размещения, перестановки, сочетания
Пусть Х = {х1 , х2 , …, хn } – множество из n элементов. Набор элементов xi1, xi2, … , xik € X называется выборкой объёма k из n элементов, или (n,k) – выборкой.
#Размещением
из n элементов по k называется упорядоченное
подмножество, состоящее из k элементов,
выбранных из множества Х. Подмножества,
отличающиеся порядком, считаются
различными. Количество таких размещений
обозначается
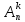 и называется коротко количеством
размещений изn
по k.
и называется коротко количеством
размещений изn
по k.
Упорядоченная выборка без повторений называется размещением из n элементов по r.
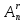 =
=
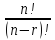 – число различных размещений.
Доказательство индукцией по k (для
произвольного п, k<=n).
k = 1. Очевидно,
– число различных размещений.
Доказательство индукцией по k (для
произвольного п, k<=n).
k = 1. Очевидно,
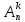 =n
, так как размещениями из п по 1 являются
подмножества в Х, состоящие из одного
элемента, а количество таких подмножеств
равно количеству элементов в Х, то есть
п. Пусть утверждение верно для k -
1. То есть для любого m>=k-1
=n
, так как размещениями из п по 1 являются
подмножества в Х, состоящие из одного
элемента, а количество таких подмножеств
равно количеству элементов в Х, то есть
п. Пусть утверждение верно для k -
1. То есть для любого m>=k-1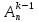 = m(m -1)(m – 2)…(m – k + 2). Докажем его для
k. Рассмотрим k мест: |1 |2|…|k-1|k|.
Произвольное размещение из n
по k получается размещением на 1-е место
любого из п элементов множества Х (таких
возможностей имеется n),
а на оставшиеся k - 1 мест - произвольного
размещения из оставшихся m = n – 1 элементов
множества Х (таких размещений имеется
= m(m -1)(m – 2)…(m – k + 2). Докажем его для
k. Рассмотрим k мест: |1 |2|…|k-1|k|.
Произвольное размещение из n
по k получается размещением на 1-е место
любого из п элементов множества Х (таких
возможностей имеется n),
а на оставшиеся k - 1 мест - произвольного
размещения из оставшихся m = n – 1 элементов
множества Х (таких размещений имеется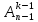 ). Отсюда
). Отсюда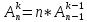 и по
предположению индукции
и по
предположению индукции
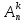 =
=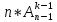 = n(n -1)(n –2)…(n – k + 1)= n! /(n – k)! .
= n(n -1)(n –2)…(n – k + 1)= n! /(n – k)! .
Упорядоченная выборка с повторениями называется размещением с повторениями из n элементов по r.
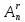 =
=
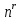 – число различных перестановок с
повторением.
– число различных перестановок с
повторением.
#Сочетанием
из n элементов
по k называется (неупорядоченное)
подмножество, состоящее из k элементов,
выбранных из множества Х. Подмножества,
отличающиеся порядком, считаются
одинаковыми. Количество таких
сочетаний обозначается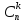 называется коротко количеством сочетаний
из п по k.
называется коротко количеством сочетаний
из п по k.
Неупорядоченная (n,r) – выборка без повторений называется сочетанием из n элементов по r.
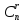 =
=
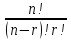 – число различных сочетаний.
– число различных сочетаний.
Доказательство.
Так как все размещения из п по k получаются
выборками из множества Х различных
сочетаний из k элементов, а затем их
всевозможными перестановками, то
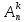 =
=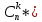 Pk
Pk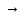 =
=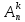 / Pk = n(n -1)(n – 2)…(n – k + 1) / k! = = n! /((n – k)!
k!) .
/ Pk = n(n -1)(n – 2)…(n – k + 1) / k! = = n! /((n – k)!
k!) .
Неупорядоченная (n,r) – выборка с повторениями называется сочетанием с повторениями из n элементов по r.
 =
=
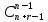 – число различных сочетаний с повторениями
– число различных сочетаний с повторениями
#Перестановкой из n элементов называется размещение из n элементов по п. Количество таких перестановок обозначается Pn.
Упорядоченная (n, n) – выборка без повторений называется перестановкой из n элементов (по n).
P
(n)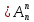 =n!
– число различных перестановок.
=n!
– число различных перестановок.
2.Бином Ньютона. Полиномиальная теорема.Свойства биномиальных коэффициентов. Треугольник Паскаля.


Полиномиальная теорема
Теорема.
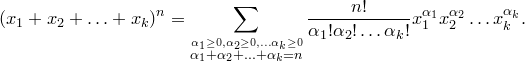
Доказательство.
![]()
![]()
Чтобы
после раскрытия скобок получился
одночлен ![]() ,
нужно выбрать те
,
нужно выбрать те ![]() скобок,
из которых берется
скобок,
из которых берется ![]() ,
те
,
те ![]() скобок,
из которых берется
скобок,
из которых берется ![]() и
т.д. и те
и
т.д. и те ![]() скобок,
из которых берется
скобок,
из которых берется ![]() .
Коэффициент при этом одночлене после
приведения подобных членов равен числу
способов, которыми можно осуществить
такой выбор.
.
Коэффициент при этом одночлене после
приведения подобных членов равен числу
способов, которыми можно осуществить
такой выбор.
Первый
шаг последовательности выборов можно
осуществить ![]() способами,
второй шаг —
способами,
второй шаг — ![]() ,
третий —
,
третий — ![]() и
т.д.,
и
т.д., ![]() -й
шаг —
-й
шаг — ![]() способами.
Искомый коэффициент равен произведению
способами.
Искомый коэффициент равен произведению