pdm_04

Множество

Кантор* определял множество как

«объединение в одно целое объектов, хорошо различимых нашей интуицией или мыслью».

A={a1, a2, a3, a4, …, an}

где: a1, a2, a3, a4, …, an – элементы множества, A – множество.

Элементы множества обычно обозначают строчными буквами, а сами множества прописными (заглавными) буквами.

*Георг Кантор - (3 марта 1845, Санкт-Петербург – 6 января 1918, Залле)

– германский математик, наиболее известен как создатель теории множеств.

2

Способы задания множеств

Перечислением

например: A ={a, b, c, d , e, f } Аналитическим выражением

например: ( x)(x ) (x(mod 2) =1) x X

Графически например:

3

Некоторые специальные множества

Ø – пустое множество, множество не содержащее ни одного элемента; U – универсум, множество всех множеств содержащее все элементы; N = {0,1,2,…} – множество натуральных чисел;

N+ = {1,2,… } – множество положительных натуральных чисел; Z = {…,-2,-1,0,1,2,…} – множество целых чисел;

Zk = Ek = {0,1,2,…,k-1} – подмножество натуральных чисел от 0 до k-1; Q = {m/n, m,n Z, n ≠ 0} – множество рациональных чисел;

R = (-∞, ∞) – множество вещественных чисел;

C= {x+j∙y, x,y R, j2=-1} – множество комплексных чисел.

Вразличных научно-практических направлениях существует значительное разнообразие специальных множеств.

4

Операции над множествами

¬ A = {x: x A } – отрицание множества A;

A B = {x: x A x B} – объединение множества A и B; A ∩ B = {x: x A x B} – пересечение множеств A и B;

A – B = A \ B = {x: x A x B} – разность множеств A и B;

A B = (A – B) (B – A) – семетрическая разность множеств A и B;

A x B = {(a,b): a A b B} – декартово произведение множеств A и B.

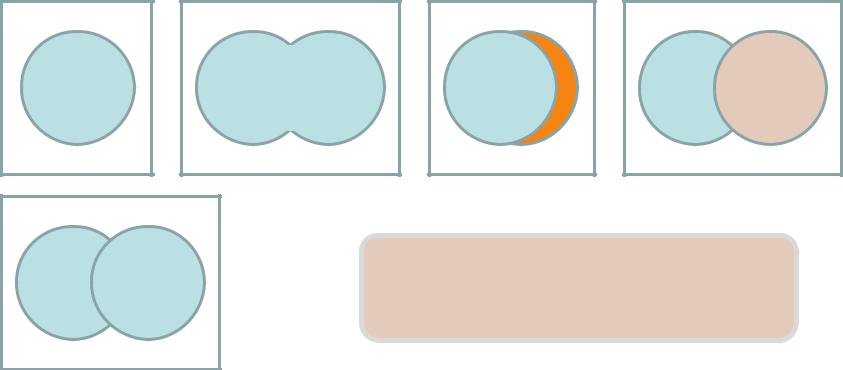
Визуализация операций на диаграммах Эйлера-Венна

¬A

Свойства операций над множествами

1.Коммутативность A B = B A, A ∩ B = B ∩ A

2.Ассоциативность A (B С) = (A B) С, A ∩ (B ∩ С) = (A ∩ B) ∩ С

3. Идемпотентность A A = A, A ∩ A = A

4.Правило поглощения A ∩ (A B) = A, A (A ∩ B) = A

5.Дистрибутивность

A ∩ (B C) = (A ∩ B) (A ∩ C) , A (B ∩ C) = (A B) ∩ (A B)

6.Инволюция (двойное отрицание) ¬(¬ A) = A

7.Свойства констант A ∩ U = A, A U = U, A ∩ Ø = Ø, A Ø = A

8. Закон исключения третьего, закон противоречия A (¬A) = U, A ∩ (¬A) = Ø

9. Закон де Моргана ¬ (A B) = (¬A) ∩ (¬B), ¬(A ∩ B) = (¬A) (¬B)

Операции над множествами ассоциированы с логическими операциями. Можно сказать, что логические операции являются частным случаем операций над множествами.

6

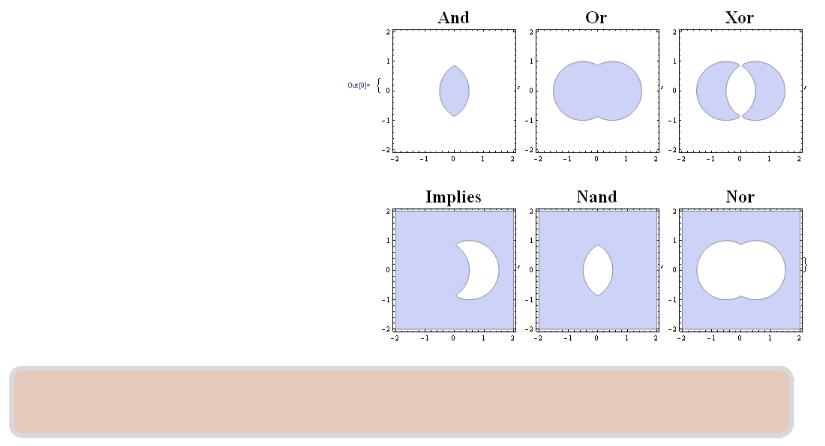
Иллюстрация связи операций над множествами с логическими операциями при помощи пакета

Mathematica

a=(-(1/2)+x)^2+y^2<1; b=((1/2)+x)^2+y^2<1; Table[RegionPlot[f[a,b],{x,-2,2},{y,-

2,2},PlotLabel→f],{f,{And,Or,Xor,Implies,Nand,Nor}}]

Результат выполнения программы

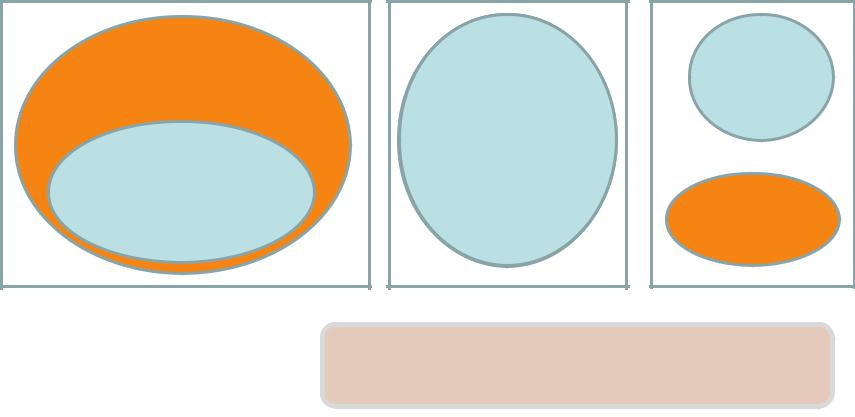
Соотношения множеств

A B = B A ↔ a (a A → a B)

A = B ↔ (A B) (B A)

A B = B A ↔ (A B) (A ≠ B)

На диаграммах Эйлера-Венна

Возможны обозначения:

A B, A B, A B, A B.

9