
pdm_06
.pdfРазностные функциональные операторы
Определение. Оператор – есть функция, которая отображает функции в функции.
Введѐм операторы
– разностный оператор |
∆ : ∆f(x) = f(x+1) – f(x) |
– оператор смещения |
E : Ef(x) = f(x+1) |
– тождественный оператор |
I : I = E – ∆ |
Ef(x) - ∆f(x) = f(x+1) – f(x+1) + f(x) = f(x).
Сучѐтом введѐнных операторов можно записать:
∆f(x) = f(x+1) – f(x) = E(f(x)) – f(x) = (E – I)(f(x)), где запись (E – I)(f(x)) означает E(f(x)) – I(f(x)).
Для операторов ∆, E, I возможно записать следующие соотношения:
∆ = E – I (E = ∆ + I) & (I = E – ∆).
В общем случае для конечных разностей справедлива операторная форма записи:
∆n(f(x)) = (E – I)n(f(x)).
21
Свойства конечных разностей
Теорема. Для действительного числа a и функций f и g, операторы ∆ и E обладают следующими свойствами:
1)∆(f + g) = ∆(f) + ∆(g) E(f + g) = E(f) + E(g)
2)∆(af) = a∆(f) E(af) = aE(f)
3)E∆ = ∆E
4)∆(a) = 0
E(a) = a
Доказательство.
1) ∆(f + g)(x) = (f(x+1) + g(x+1)) – (f(x) + g(x)) = (f(x+1) – f(x)) + (g(x+1) – g(x)) = = ∆f(x) + ∆g(x)
E(f + g)(x) = f(x+1) + g(x+1) = Ef(x) + Eg(x)
2)∆(af )(x) = (af(x+1) – af(x)) = a∆f(x) E(af )(x) = aEf(x)
3)E∆f(x) = E(f(x+1) – f(x)) = ∆Ef(x)
4)т.к. a = const. т.е. a не зависит от x E(a) = a и ∆(a) = a – a = 0
22
Конечные разности и дифференциал
Известно, что производная функции f (x) |
|
|||||||
определена как : |
|
|
|
|
|
|||
f x (x) |
df (x) |
lim |
f (x |
x) |
f (x) |
lim |
|
f (x) |
dx |
|
x |
|
|
x |
|||
|
x 0 |
|
x 0 |
|||||
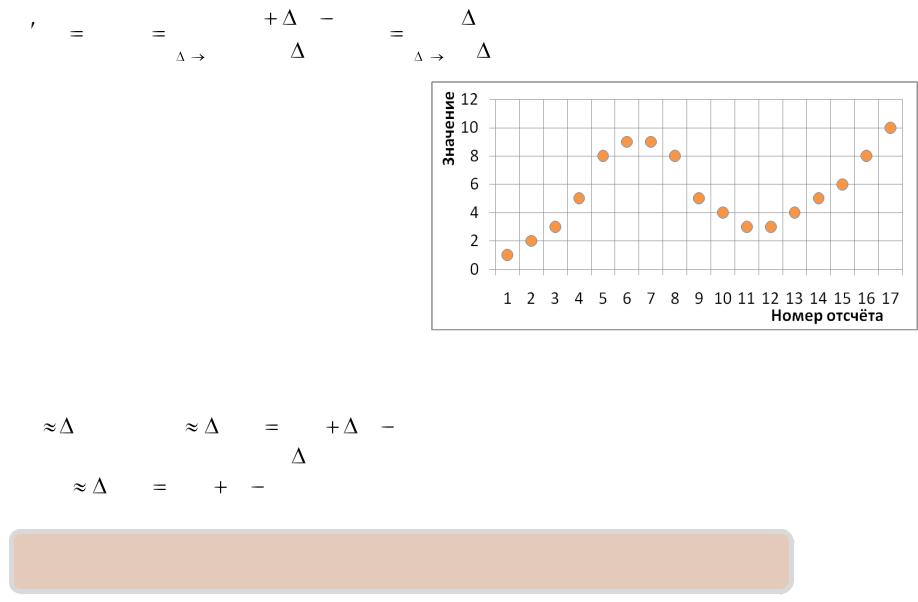
В вычислительных машинах функции задаются отсчѐтами с дискретным шагом или функциональным выражением позволяющим вычислить значение функции с некоторой точностью, дискретной точностью определяемой форматом данных.
В вычислительных машинах дифференциал вычисляют |
|||
при помощи конечных |
разностей, полагая: |
||
dx |
x и df (x) f (x) |
f (x |
x) f (x), |
переходя от приращения x |
к отсчѐтам, получим: |
||
df (x) |
f (x) f (x 1) |
f (x). |
|
Точность вычисления дифференциала при помощи конечных
разностей определяется частотой отсчѐтов. |
23 |
|
Вычисление дифференциала с помощью конечных
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разностей |
|
|
|
Например, |
для |
уравнения |
Лапласа в |
|
|
|
|||||||||||||
двумерном |
пространст ве |
x0 y : |
|
|
|
|
|
|
|||||||||||
2 f(x,y) |
|
|
|
2 f(x,y) |
0 |
|
|
|
|
|
|
|
|
|
|||||
|
x2 |
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При переходе |
к |
|
|
конечным |
разностям получим |
|
|
||||||||||||
2 f(x,y) |
|
|
|
2 f(x,y) |
|
|
|
|
|
|
|
|
|
|
|||||
|
x2 |
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x Δx,y) |
2 f (x,y) |
f (x |
Δx,y) |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
f (x,y |
Δy) |
2 f (x,y) |
f (x,y |
Δy) |
|
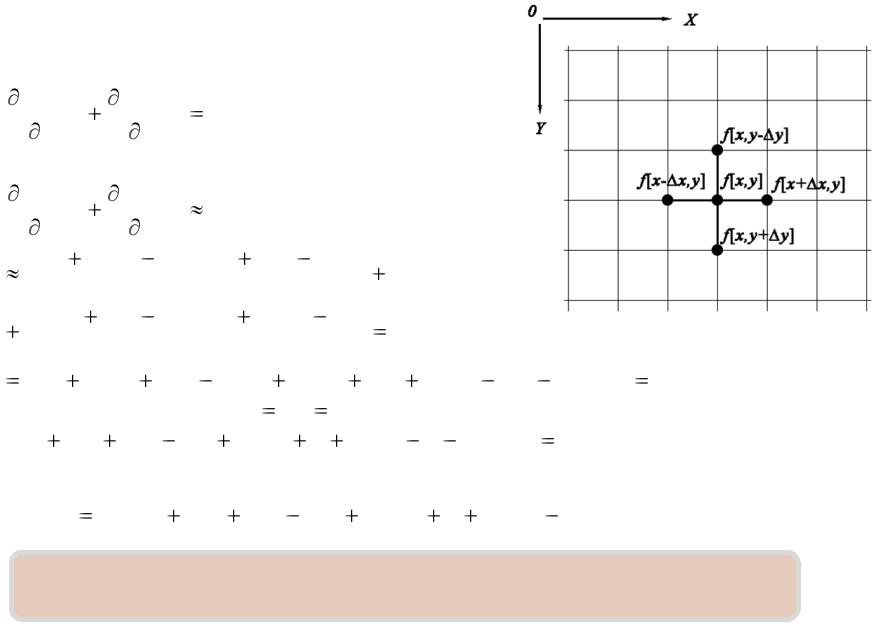
Шаблон дифференцирования |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 y |
|
|
|
|
|
|
|
||
|
f (x Δx,y) f (x Δx,y) |
|
f (x,y |
|
Δy) f (x,y Δy) |
4 f (x,y) |
0 |
||||||||||||
полагая |
шаг |
сетки : Δx |
Δy |
1, |
запишем : |
|
|
||||||||||||
f (x 1,y) |
|
|
|
f (x 1,y) |
f (x,y |
1) |
|
f (x,y 1) |
4 f (x,y) |
0 |
|
||||||||
Из полученног о разностног о |
уравнения |
возможно |
выразить f (x, y) : |
||||||||||||||||
f (x, y) |
1 |
|
( f (x |
1, y) |
f (x |
1, y) |
|
f (x, y |
1) f (x, y |
1)) |
|
||||||||
4 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При других шаблонах дифференцирования разностная схема может |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
отличаться от приведенной. |
24 |
|||||||
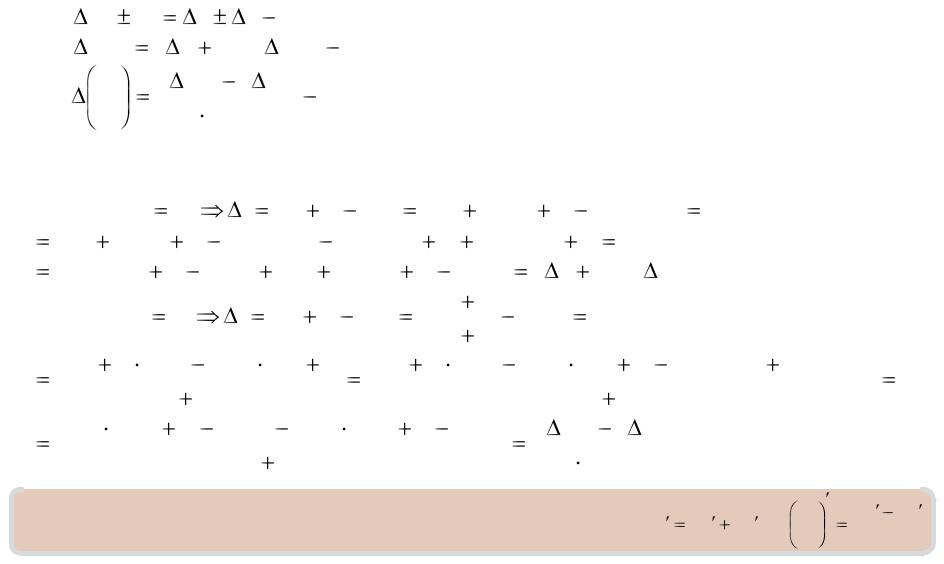
Сумма, произведение и частное
Теорема. |
Для функций |
f |
и g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
справедлив ы следующие выражения : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1) |
|
( f |
g) |
|
f |
|
g |
|
правило суммы |
и разности; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2) |
( fg) |
|
f |
g |
E(g) ( f ) |
|
правило произведен ия; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3) |
|
|
f |
|
g |
( f ) |
f |
(g) |
правило |
|
частного. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
g |
|
|
g (E(g)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1) См. слайд "Свойства к.р." |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2) |
Пусть t |
|
fg |
|
t |
|
t(x |
1) |
t(x) |
|
f (x |
1)g(x |
1) |
f (x)g(x) |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
f (x 1)g(x 1) |
|
f (x)g(x) |
|
f (x)g(x 1) |
f (x)g(x 1) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
f (x)(g(x |
1) |
|
g(x)) |
|
g(x |
1)( f (x |
1) |
f (x)) |
|
f |
g |
E(g) ( f ) |
|
|
|
|
|
|
|
||||||||||||||||
3) |
|
Пусть t |
|
f |
|
t |
t(x |
1) |
t(x) |
|
f (x |
1) |
|
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
g |
|
|
g(x |
1) |
|
|
|
g(x) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
f (x 1) g(x) |
f (x) g(x 1) |
|
f (x 1) g(x) |
f (x) g(x 1) |
f (x)g(x) |
|
f (x)g(x) |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
g(x 1)g(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x 1)g(x) |
|
|
|
|
|
|
|
|||||||||
|
|
|
g(x) ( f (x 1) |
|
f (x)) |
f (x) (g(x 1) g(x)) |
|
g ( f ) |
f (g) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
g(x 1)g(x) |
|
|
|
|
|
|
|
|
|
|
g (E(g)) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Напомним выражения |
для произведен ия и частного производно й : |
( fg) |
fg gf |
и |
|
f |
|
gf |
fg |
|||||||||||||||||||||||||||||
|
g |
|
|
g 2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
25
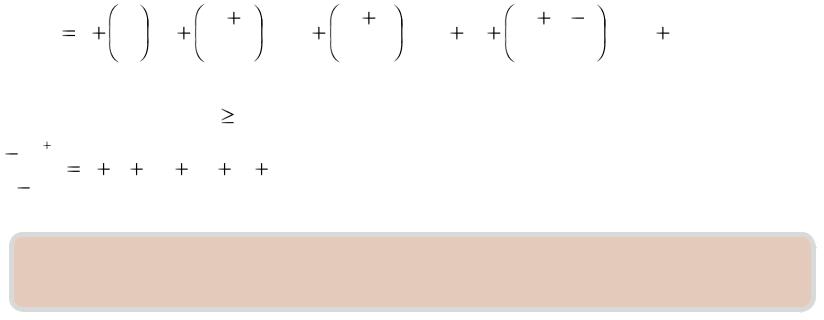
Производящие функции
|
Определение. Назовѐм выражение a |
0 |
+ a x + a x2 |
+ a x3 + . . . + a xn + . . . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
n |
|
|
производящей функцией последовательности a0, a1, a2, …, an, … |
||||||||||||||||||||||
|
Пусть f(x) и g(x) многочлены, определим отношение |
|
|||||||||||||||||||||
|
f(x)/g(x) = a |
0 |
+ a x + a x2 |
+ a x3 |
+ . . . + a xn + . . . |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
|
|
n |
|
|
|
|
|
|
тогда и только тогда когда: |
|
|
|
|
|
|
|
|
||||||||||||||
|
f(x) = g(x)(a |
+ a x + a x2 |
+ a x3 |
+ . . . + a xn |
+ . . . ). |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
2 |
|
3 |
|
|
|
n |
|
|
|
|
|
Определение. Если f(x)/g(x) = a + a x + a x2 + a x3 |
+ . . . + a xn + . . ., то |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
2 |
|
3 |
|
n |
|
a |
0 |
+ a x + a x2 + a x3 + . . . + a xn + . . . называется разложением f(x)/g(x). |
||||||||||||||||||||
|
|
|
|
1 |
|
|
|
2 |
|
|
3 |
|
n |
|
|
|
|
|
|
|
|
||
Теорема. Для любого m имеет место |
|
разложение |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
m |
ax |
m |
1 |
a2 x2 |
m |
2 |
a3 x3 |
... |
m |
n 1 |
an xn ... |
||
|
(1-ax)m |
|
1 |
2 |
|
3 |
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Теорема. При всех n |
0 |
имеем : |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
xn |
1 |
|
1 |
x |
x2 |
x3 ... |
xn . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подробнее о производящей функции возможно посмотреть у Дж. Андерсона (см. список литературы).
26

Применение производящей функции для решения
рекуррентных отношений
Пример.
Найти функцию, заданную рекуррентным отношением:
a0 = 5;
ak = ak-1 + 3.
Запишем ak - ak-1 – 3 = 0.
Полагая, что: f(x) = a0 + a1x + a2x2 + a3x3 + . . . + anxn + . . . и учитывая,
что при ak-1 |
коэффициент |
равен 1, требуется найти: |
|||
xf(x) = a x+ a x2 |
+ a x3 |
+ a |
x4 + . . . + a xn+1 |
+ . . . |
|
0 |
1 |
2 |
3 |
n |
|
Кроме, того запишем производящую функцию, с коэффициентом 3 при каждом
члене:
3/(1–x)= 3 + 3x + 3x2 + 3x3 + . . . + 3xn + . . .
Далее f(x) – xf(x) – 3/(1–x) = a0 – 3 + (a1 – a0 – 3)x + (a2 – a1 – 3)x2 + . . . + (an
– 3)xn + … , т.к. ak - ak-1 – 3 = 0 при всех , k ≥ 1 запишем: f(x) – xf(x) – 3/(1-x) = a0 – 3 = 2. (*)
Решим полученное (*) уравнение относительно f(x):
f(x) = 3/(1-x)2 + 2/(1 – x) = 3(1 + 2x + 3x2 + . . . + (n+1)xn + . . .) +
+ 2(1 + x + x2 + . . . + xn + . . .) = 5 + 8x + 11x2 + 14x3 + . . . + (3n + 5)xn + . . ..
Искомое выражение будет иметь вид: an = 3n + 5.
Подробнее по теме возможно посмотреть у Дж. Андерсона (см. список литературы).
– an-1
27

Рекурсия в программировании
Зачастую при рекурсии удаѐтся получить решение некоторой задачи которое возможно выразить лаконичным формальным выражением. Если рекуррентная функция вызывается множество раз, то вычислительное устройство при каждом вызове функции копирует параметры функции, ! создаѐт для каждой вызванной функции новый набор локальных переменных и констант, сохраняет адрес возврата и параметры (набор переменных и констант) для каждой вызвающей функции. Таким образом происходит быстрое расходование оперативной памяти. Практика показывает, что если рекурсивный вызов происходит более 5-8 раз то применение рекурсии неэффективно с точки зрения расхода вычислительных ресурсов.
В каждом конкретном случае следует принимать решение о применении или исключении рекурсии на основе анализа алгоритмов и программ и методов оптимизации программного обеспечения.
28

Алгоритм Эвклида (рекурсивная реализация)
//Рекурсивное вычисление НОД(k,n) C++ #include <iostream> //------------------------------
//int64
typedef unsigned long long int uint; // функция отыскания НОД(k,n)
uint gcd(uint k, uint n) { return((!n)?k:gcd(n,k%n));
}
Пример. Выполнения программы
Enter number: k = 512
n = 34 GCD = 2
using namespace std;
// главная функция int main() {
uint k, n;
cout<<"Enter number:"<<endl; cout<<"k = ";
cin>>k; cout<<"n = "; cin>>n;
cout<<"GCD = "<<gcd(k,n)<<endl; // ожидаем нажатия клавиши ввод system("pause");
return 0;
}
//-----------------------------
В лекции 8 возможно найти нерекурсивную
реализацию алгоритма Эвклида. |
29 |
|

Вычисление факториала
// Рекурсивное вычисление факториала C++ |
|
|
#include <iostream> |
Пример. Выполнения программы (int32) |
|
//--------------------------------------------------- |
Enter number: |
|
// определяем тип long long int (int64) |
n = 14 |
|
typedef unsigned long long int uint; |
factorial(0) = 1 |
|
// функция вычисления факториала |
||
factorial(1) = 1 |
||
// переполнение при int 32b после n>12 |
||
factorial(2) = 2 |
||
// при при int 64b после n>20 |
||
|
||
uint f(uint n) {return((!n)?1:n*f(n-1));} |
factorial(3) = 6 |
|
|
factorial(4) = 24 |
|
using namespace std; |
factorial(5) = 120 |
|
// главная функция |
factorial(6) = 720 |
|
int main() { |
||
factorial(7) = 5040 |
||
uint n; |
||
factorial(8) = 40320 |
||
cout<<"Enter number:"<<endl; |
||
|
||
cout<<"n = "; |
factorial(9) = 362880 |
|
cin>>n; |
factorial(10) = 3628800 |
|
for(uint i = 0; i <= n; i++ ) { |
factorial(11) = 39916800 |
|
cout<<"factorial("<<i<<") = "<<f(i)<<endl; |
factorial(12) = 479001600 |
|
} |
||
factorial(13) = 1932053504 |
||
// ожидаем нажатия клавиши ввод |
||
factorial(14) = 1278945280 |
||
system("pause"); |
||
|
||
return 0; |
|
}
Следует помнить о быстром переполнении разрядной сетки (регистров, ячеек памяти) при вычислении факториала!
Нерекурсивное вычисление факториала на C++
for( uint k=1, uint i=1; i<=N; i++) k *= i; |
30 |
|
