
pdm_06
.pdf
Множество Мандельброта
Определение. Множество Мандельброта определено следующим рекурентным выражением: zn+1=zn2+c которое является ограниченным при z0=0, т.е. это такое множество для которого существует такое действительное R, что неравенство |zn+1|<R выполняется при всех натуральных n.
На комплексной плоскости множество Мандельброта возможно построить при помощи выражения:
x |
x 2 |
y |
2 |
p |
, где |
n 1 |
n |
n |
|
|
|
|
|
|
|||
yn 1 |
2xn yn |
q |
|
|
|
zn xn |
j yn ; c p j q |
||||
Фрактальная геометрия нашла широкое применение в самых разных областях знаний человека.
11
Цепные дроби
Определение. Для конечной последовательности t0, t1, t2, . . . , tn действительных чисел, где n ≥ 0 и ti > 0 для i ≥ 1, определим конечную цепную
дробь [t0; t1, t2, . . . , tn] следующим образом:
[t0;] = t0;
[t0; t1] = t0 + 1/ t1;
[t0; t1, t2, . . . , tk]; = [t0; [ t1; t2, . . . , tn]] для 1 < k ≤ n.
Числа t0, t1, t2, . . . , tn называются неполными частными, или элементами цепной дроби. Цепная дробь [t0; t1, t2, . . . , tn] называется простой, если – целое число для каждого i, т.е. каждый элемент цепной дроби есть целое
число. Если x – действительное число и x= [t0; t1, t2, . . . , tn], то [t0; t1, t2, . . . , tn] есть представление числа x цепной дробью.
Цепную дробь x [t0 ;t1, t2 ,..., tk 1, xk ] возможно записать в виде выражения :
x t0 |
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
1 |
|
|
||
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
1 |
|
|
||
|
|
|
|
|
||
|
|
2 |
|
|
|
|
1 |
|
|
||||
t3 ... |
|
|
|
tk 1 |
1 |
|
|
|
|
||
|
|
|
|
|
xk |
|
|
|
|
|
Теорема. Цепная дробь периодична (т.е. последовательность еѐ элементов повторяется, начиная с некоторого элемента), тогда и только тогда, когда число, представленное этой дробью – квадратическая иррациональность, т.е. число вида: a + b(c1/2), где a,b,c – рациональные числа.
Пример. Золотое сечение
(51/2+1)/2 = [1;1,1,1,…]=[1;(1)]
12
Для иррационального числа процесс разложения в цепную дробь можно продолжать бесконечно.

Разложение обыкновенных дробей в цепную дробь
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
47 |
|
2 |
13 |
|
|
2 |
1 |
|
|
|
2 |
|
|
1 |
|
2 |
|
1 |
|
|
|
... |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
17 |
|
17 |
|
|
17 |
|
|
|
|
|
4 |
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
13 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
[2;1,3,4] [2;1,3,3,1] |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
3 |
|
1 |
|
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
|
|
|
Пример. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
120 |
|
|
|
25 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
5 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
|
|
29 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5 |
|
|
1 |
|
|
[ |
|
|
|
|
|
||
1 |
|
1 |
|
|||
|
|
|
|
|||
|
|
|
|
|
||
6 |
|
1 |
|
|
|
|
|
|
|
||
3 |
1 |
||||
|
|||||
|
|
|
|
||
|
1 |
||||
|
|
||||
|
1 |
|
|
5 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
|
|
1 |
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
25 |
|
|
|
6 |
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
4 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
5;1, 6, 4] |
[ 5;1, 6, 3,1] |
|||||||||||
π ≈ [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, . . .]. |
13 |

Разложение рациональных функций в цепные дроби
Для рациональн ой функции
f (x) |
c10 |
c11x c12 x2 ... |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
c00 |
c01x c02 x2 ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
произведя |
элементарные преобразов ания получим |
|
|||||||||||||||||||||||||
f (x) |
|
c10 |
|
|
, где f1 (x) |
|
c20 |
c21x |
|
c22 x2 ... |
, |
|
|||||||||||||||
c00 |
|
|
|
|
|
c10 |
c11x |
|
c12 x2 ... |
|
|
||||||||||||||||
|
|
xf1 (x) |
|
|
|
|
|
||||||||||||||||||||
в общем случае коэффициен ты вычисляют |
по формуле : c jk |
c j 2,0 |
|||||||||||||||||||||||||
c j 1,0 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в результате разложения |
получим конечную цепную дробь вида : |
||||||||||||||||||||||||||
f (x) |
|
|
|
c10 |
|
|
|
|
|
|
0; |
c10 |
, |
c20 x |
, |
c30 x |
,..., |
cn0 x |
|
|
|||||||
|
|
|
c20 x |
|
|
|
|
|
|
|
|
||||||||||||||||
|
c00 |
|
|
|
c |
c |
|
c |
|
|
|
c |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
00 |
|
|
10 |
|
|
20 |
|
|
|
n 1,0 |
|
|
||||
|
|
|
с10 |
|
с30 x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
c20 ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
c j |
2,k |
1 |
, j 2 |
c j |
|
|
|
1,k |
1 |
|
Пример. Разложить в цепную дробь |
|
|
|
|
|
Вычислим коэффициенты |
|
||||||||||||||||||
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cjk |
k=0 |
k=1 |
k=2 |
|
|
|
1 5x |
6x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
j=0 |
1 |
-5 |
6 |
|
|
|||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4x |
|
|
2x |
12 x |
|
|
|
|
|
|
|
|
|
j=1 |
1 |
-1 |
0 |
|
|
||||||
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j=2 |
-4 |
6 |
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f (x) 0;1 , |
1 |
, |
|
4 , |
2 |
|
|
|
|
4x |
|
|
|
|
|||||||||||
|
1 |
|
|
|
|
|
|
j=3 |
-2 |
0 |
0 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
j=4 |
-12 |
0 |
0 |
|
14 |
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
6x |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Подходящие дроби
Определение. Числа [t0;], [t0; t1], … , [t0; t1, t2, . . . , tk], … , [t0; t1, t2, . . . , tn]
называют подходящими дробями цепной дроби [t0; t1, t2, . . . , tn]. Где [t0; t1, t2, . . . , tk] есть k-ая подходящая дробь при 0 ≤ k ≤ n.
Определение. Будем говорить, что две цепные дроби [t0; t1, t2, . . . , tn] и [b0; b1, b2, . . . , bm] равны почленно, если n=m и ti=bi при 0 ≤ i ≤ n.
Теорема. Пусть n – есть неотрицательное целое число и [t0; t1, t2, . . . , tn] – конечная цепная дробь, которая рекурсивно определяет конечные последовательности p0, p1, . . . , pn и q0, q1, . . . , qn следующим образом:
1)p0 = t0 q0 = 1
2)p1 = t0t1 + 1 q1 = t1
3)pk = pk-1tk + pk-2
qk = qk-1tk + qk-2 при 2 ≤ k ≤ n
Тогда qk > 0 и [t0; t1, t2, . . . , tk] = pk/qk при 0 ≤ k ≤ n.
15
Исчисления цепных и подходящих дробей
Пример.
Вычислить цепную дробь
105 |
3 |
|
|
1 |
|
|
|
|
|
|
|
29 |
1 |
1 |
|
||
|
|
||||
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
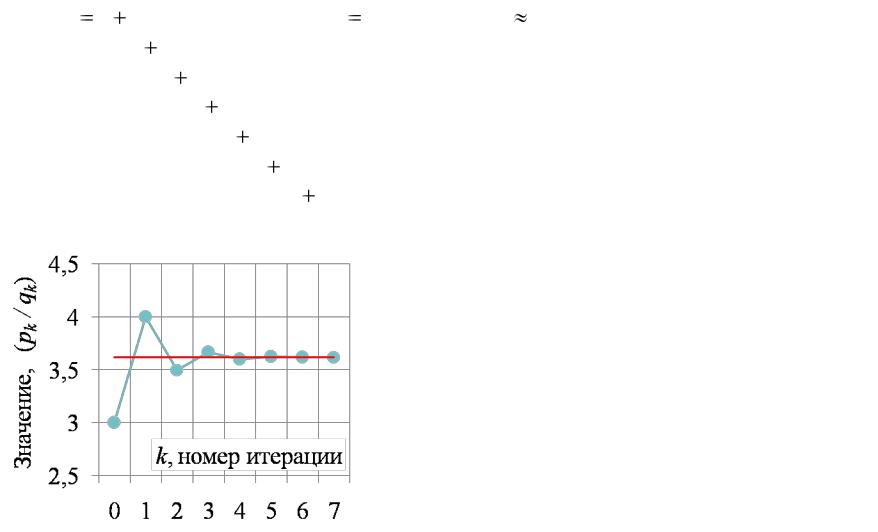
[3;1,1,1,1,1, 2,1] |
3,62068965 |
Пример. Для дроби [3; 1, 1, 1, 1, 1, 2, 1]
вычислить подходящие дроби.
В соответствии с рекуррентными выражениями
1)p0 = t0 q0 = 1
2)p1 = t0t1 + 1 q1 = t1
3)pk = pk-1tk + pk-2
|
|
qk = qk-1tk + qk-2 |
при 2 ≤ k ≤ n |
|
|
|
|||||
производим вычисления (в таблице) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
– 1 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
tk |
|
|
3 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
|
pk |
|
1 |
3 |
4 |
7 |
11 |
18 |
29 |
76 |
105 |
|
qk |
|
0 |
1 |
1 |
2 |
3 |
5 |
8 |
21 |
29 |
16

Разложение функции ex в цепную дробь
Для |
|
функции ex Эйлер получил разложение |
||||||||||||||||||||
ex |
0; |
1 |
, |
|
|
2x |
, |
x2 |
, |
x2 |
,..., |
x2 |
|
,... |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 |
|
2 |
x |
6 |
10 |
|
|
4n |
2 |
|
||||||||
Подходящие |
дроби будут иметь вид |
|||||||||||||||||||||
p1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
p2 |
|
|
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
q2 |
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||
p |
12 |
|
|
6x |
x2 |
|
|
|
|
|
|
|
||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
12 |
|
|
6x |
x2 |
|
|
|
|
|
|
|
||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p4 |
|
120 |
|
|
|
60 x 12 x2 |
x3 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
q4 |
|
120 |
|
|
|
60 x |
|
12 x2 |
x3 |
|
|
|
||||||||||
...
В частном случае,
полагая |
x 1.0, получим |
|||
e |
193 |
|
2,7183 ... |
|
|
|
|
||
71 |
|
|||
|
|
|
||
17
Конечные разности
Определение. Конечная разность – есть разность между соседними членами какой-нибудь последовательности или между значениями функции в точках, расположенных с постоянным интервалом в некотором пространстве.
Определение. Первая разность, или разность первого порядка функции f,
обозначаемая ∆f определена следующим образом:
∆f(x) = f(x+1) – f(x),
где f(x) и f(x+1) есть значения функции f в соседних точках x и x+1, соответственно. Собственно тоже можно сказать для любых значений функции f(x+n) и f(x+n+1) в точках x+n и x+n+1, где x,n Z, а 1 – шаг разности.
Вторая разность, или разность второго порядка функции f, обозначаемая ∆f
определена следующим образом:
∆2f(x) = ∆(∆f(x)), т.е.:
∆2f(x) = ∆f(x+1) – ∆f(x) = (f(x+2) – f(x+1)) – (f(x+1) – f(x)) = f(x+2) – 2f(x+1) + f(x).
В общем случае n-ая разность, или разность n-го порядка, обозначается ∆nf(x) и определяется индуктивно выражением:
∆nf(x) = ∆(∆n-1f(x)).
18

|
Разностные формулы прядка n |
|
|
|
|
порядок |
формула |
|
1 |
∆f(x) = |
|
= f(x+1) – f(x) |
||
|
||
2 |
∆∆f(x) = ∆2f(x) = (f(x+2) – f(x+1)) – (f(x+1) – f(x)) = |
|
= f(x+2) – 2f(x+1) + f(x) |
||
|
||
3 |
∆3f(x) = (f(x+3) – 2f(x+2) + f(x+1)) – (f(x+2) – 2f(x+1) + f(x)) = |
|
= f(x+3) – 3f(x+2) + 3f(x+1) - f(x) |
||
|
||
|
∆4f(x) = |
|
4 |
=(f(x+4) – 3f(x+3) + 3f(x+2) - f(x+1)) – (f(x+3) – 3f(x+2) + 3f(x+1) - f(x)) = |
|
|
= f(x+4) – 4f(x+3) + 6f(x+2) – 4f(x+1) + f(x) |
В общем случае
|
|
n |
|
n |
|
n |
f (x) |
( 1) |
k |
f (x n k), где |
|
|
|
k |
|||
|
k |
0 |
|
|
|
|
|
|
|
формула расчѐта биномиальных коэффициентов
n |
|
n! |
|
|
|
k |
|
|
, n, k целые неотрицательные |
||
|
k!(n k)! |
||||
В разностных формулах знаки чередуются |
|
1 |
|||
(начинаются с плюса), функциональные |
|
||||
|
|
||||
элементы умножаются на биномиальные |
|
1 |
|||
|
коэффициенты, которые возможно |
... |
... |
||
|
вычислить с помощью треугольника |
||||
|
|
|
|||
Паскаля.
Треугольник Паскаля |
|
|
|||
|
|
1 |
|
|
|
|
1 |
1 |
|
|
|
|
1 |
2 |
1 |
|
|
1 |
3 |
3 |
1 |
|
|
|
4 |
6 |
4 |
1 |
|
5 |
10 |
10 |
5 |
|
1 |
|
... |
... |
... |
... |
... |
|
|
|
|
|
19 |
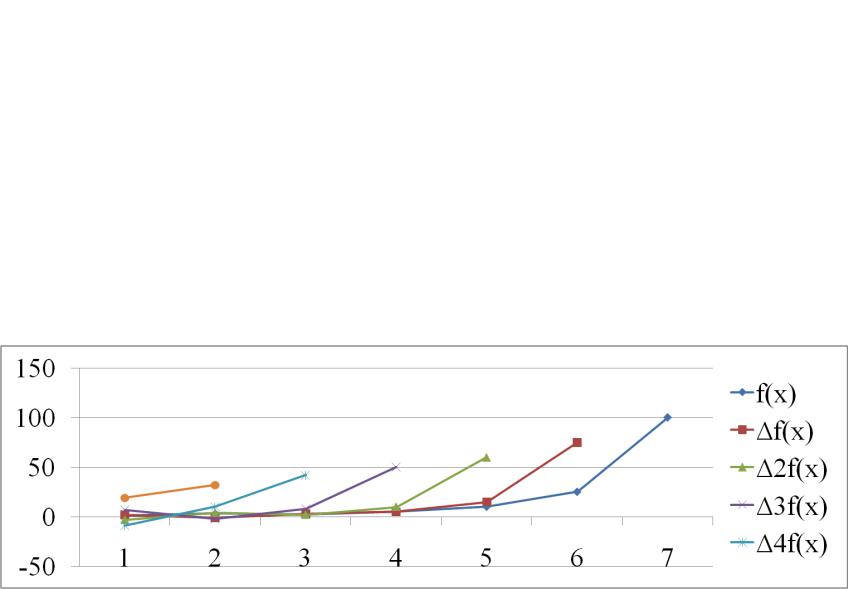
Вычисление конечных разностей
x |
f(x) |
∆f(x) |
∆2f(x) |
∆3f(x) |
∆4f(x) |
∆5f(x) |
1 |
1 |
2 |
-3 |
7 |
-9 |
19 |
2 |
3 |
-1 |
4 |
-2 |
10 |
32 |
3 |
2 |
3 |
2 |
8 |
42 |
|
4 |
5 |
5 |
10 |
50 |
|
|
5 |
10 |
15 |
60 |
|
|
|
6 |
25 |
75 |
|
|
|
|
7 |
100 |
|
|
|
|
|
прим. |
& |
& |
& |
& |
|
|
|
|
|
|
|
|
|
20
