
ДС Радиооптика_1 / Литература ч.1 / Романов, Стальмакова
.pdf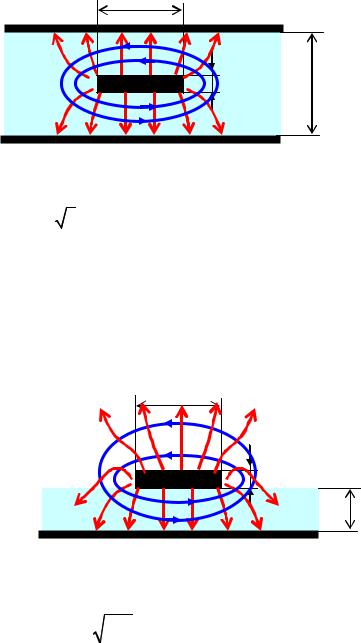
10)Полосковые линии передачи. Структура поля основных типов волн в симметричной и несимметричной линиях. Эффективная диэлектрическая проницаемость, волновое сопротивление, частотный диапазон полосковых линий.Область применения полосковых линий передачи.
Большое распространение при конструировании высокочастотной техники нашли полосковые линии передачи. Они хорошо интегрируются с активными и пассивными элементами трактов. В симметричной полосковой линии основной волной является волна типа T
W
t
b
ε
- симметричная
Постоянная распространения в симметричной полосковой линии передачи
β = |
2π |
|
|
. |
|
|
ε |
||||
λ |
|||||
|
|
|
|
Преимущество несимметричной линии обусловлено хорошей интеграцией с активными и пассивными элементами, устанавливаемыми на СВЧ платы, выполненные по полосковой технологии. В микрополосковой линии распространяется квази-T волна. С увеличением частоты наблюдается дисперсия постоянной распространения, обусловленная тем, что волна распространяется в двух средах: диэлектрической подложке и воздухе (рис. 4.7). На относительно невысоких частотах этой дисперсией пренебрегают.
|
W |
ε=1 |
t |
|
|
ε |
d |
|
-несимметричная
Постоянная распространения рассчитывается по формуле
β = |
2π |
|
|
|
|
|
|
ε |
|
. |
|||
λ |
эф |
|||||
|
|
|
|
|||
|
|
|
|
|
где эффективная диэлектрическая постоянная
εэф = |
ε + 1 |
+ |
ε −1 |
|
+ |
10d −1/ 2 |
||
2 |
2 |
1 |
|
|
|
|||
|
|
|||||||
|
|
|
|
|
W |
|||

Важным достоинством полосковых линий является возможность получения волновых сопротивлений в широком диапазоне значений. Со стороны больших сопротивлений ограничение состоит в технологических возможностях изготовления тонких линий. Со стороны малых волновых сопротивлений ограничение состоит в том,
чтобы ширина линии была меньше четверти волны в линии на рабочей частоте.
|
|
|
|
|
|
|
4(b − t ) |
|
|
|
|
|
|
|
|
|
|
|
120 |
|
8(b − t ) |
|
8 |
(b − t ) 2 |
|
||||||||||
|
|
|
|
|
|
||||||||||||
ρ = |
|
|
|
|
ln 1 |
+ |
|
|
|
+ |
|
|
|
|
+ 6, 27 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
ε |
|
|
πW ′ |
πW ′ |
|
|
πW ′ |
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где эффективная ширина линии, обусловленная краевым эффектом
W ′ =W + W ,

11)Симметричная двухпроводная линия передачи. Основная волна Т: волновое сопротивление, затухание, мощность.Область применения двухпроводных
линий.
Двухпроводная симметричная линия состоит из двух параллельных проводников, как правило, круглого поперечного сечения. Основным типом колебаний такой линии является волна типа T. Структура электромагнитного поля и геометрические размеры приведены на рис 4.3. Двухпроводная линия является линией открытого типа (неэкранированной). Электромагнитное поле почти полностью сосредоточено внутри
окружности с радиусом r = (5 ÷ 6) D .
E


 H d
H d 


D
Излучение линии практически отсутствует, если выполняется условие D < 0,1λ .
Этим соотношением определяется диапазон рабочих частот двухпроводной линии.
Фазовая скорость волны T вдоль двухпроводной линии равна скорости света c =
3·108 м/с.
Волновое сопротивление линии определяется формулой
|
2D |
|
2D |
||
r =120ln |
|
|
= 276lg |
|
. |
|
|
||||
|
d |
|
d |
||
Практические значения волнового сопротивления линии лежат в диапазоне 400 – 600
Ом.
Затухание двухпроводной линии определяется конечной проводимостью материала
проводников. Например, для меди
|
дБ |
|
0,104 |
|
|
2D |
|||
a |
|
|
= |
|
|
|
ln |
|
|
|
|
|
|
|
|||||
|
d |
l0 |
|||||||
|
м |
|
|
|
d |
||||
Часто двухпроводная линия выполняется в диэлектрической оболочке. Влияние диэлектрика приводит к уменьшению длины волны в линии.
Двухпроводная линия используется в диапазоне от коротких до дециметровых волн.
Для снижения уровня помехового излучения и приема, двухпроводную линию
закручивают, получая линию «витая пара».
P = |
U 2 |
× |
|
е |
|
|
× |
1 |
-мощность |
120 |
|
м |
ln(D d ) |
||||||
12) Объёмные резонаторы, образованные на основе линий передачи.Классификация типов колебаний в объёмных резонаторах, их резонансные частоты.Основной тип колебаний, вырожденные колебания.
Поле в отсеченной области, в дополнение к свойственным данной линии передачи граничным условиям, должно удовлетворять также условию Et =0 на введенных перегородках, где Et – тангенциальная компонента.
Объемные прямоугольные резонаторы выполняют на основе прямоугольных волноводов замыканием проводящими плоскостями стенок волновода. Тип колебания в резонаторе обозначают с помощью буквы и трех индексов, например, Hmnp . Буква
говорит о том, какая из компонент электрического или магнитного поля имеет составляющую, параллельную оси z . Индексы показывают число вариаций компонентов поля соответственно вдоль оси x y и z .
Дальнейшее увеличение рабочей частоты резонатора обеспечивается деформацией резонатора и преобразованием его, например, в сферу (рис.6.5). В таком резонаторе электрическое и магнитное поле существует в одной области, чередуясь во времени. Данный резонатор называется объемным резонатором. Объемные резонаторы имеют очень высокую добротность. Примерно оценить добротность резонатора можно по формуле
Q ≈ |
V |
, |
(6.2) |
|
|||
|
ДS |
|
|
где Д глубина скин-эффекта. Добротность резонатора зависит от типа колебания. Объемные резонаторы строятся на основе линий передачи диапазона СВЧ.
Способ возбуждения колебаний в объемных резонаторах тот же, что и в линиях передачи. Элементами связи могут быть штыри, петли и щели.
Критерии объемного резонатора: размер его соизмерим или больше длины волны; Эл-е и магнитное поля существуют в одном и том же объеме, но чередуются во времени. Скин эффект – амплитуда поля убывает в е раз. Объемные резонаторы всегда выполняются на отрезках линий передач.
По аналогии с волноводами типы колебаний в О. р. классифицируются по группам в зависимости от того, имеет ли пространственное распределение электромагнитного поля осевые или радиальные (поперечные) компоненты. Колебания типа Н (или ТЕ) имеют осевую компоненту лишь магнитного поля; колебания типа Е (или ТМ) обладают осевой компонентой только электрического цоля. Наконец, у колебаний типа ТЕМ ни электрическое, ни магнитное поля не имеют осевых компонентов. Примером О. р., в котором могут возбуждаться колебания ТЕМ-типа, может служить полость между двумя коаксиальными проводящими цилиндрами, ограниченная с торцов плоскими проводящими стенками, перпендикулярными оси цилиндров.
О. р. широко применяются в технике в качестве колебательных систем генераторов (клистронов, магнетронов и др.), фильтров, эталонов частоты, измерительных контуров, а также различных устройств для исследования твердых, жидких и газообразных веществ. О. р. применимы для частот 109—1011 гц.
Может оказаться, что два различных типа колебаний имеют одинаковые частоты. Такие колебания называются вырожденными. Их появление в резонаторе крайне нежелательно, т.к. малейшая неоднородность снимает вырождение, и в итоге появляются два колебания с близкими частотами.
Колебание с минимальной собственной частотой называется основным типом колебаний, остальные – высшими типами колебаний.
Переменное поле в резонаторе без потерь называют собственным колебанием резонатора (по аналогии с собственными волнами направляющей структуры). Из (8.2) следует, что число р определяет количество полуволн стоячей волны вдоль резонатора.

Таким образом разным значениям р будут соответствовать разные собственные колебания. Частоты этих колебаний называют собственными частотами резонатора.
Набор всех собственных частот составляет спектр колебаний резонатора. Для прямоуг-го:
как следует из (8.9), при n, m, p > 1 собственные частоты Enmp и Hnmp колебаний одинаковы, т.е. эти колебания являются вырожденными. Е-колебаний с индексами n=0 или m=0 не существует, т.к. нет соответствующих собственных волн. Поэтому при нулевых значениях n или m возможны только Н-колебания и вырождение отсутствует.

13) Типы объёмных резонаторов: прямоугольный, цилиндрический, коаксиальный и полосковый. Основные типы колебаний в этих резонаторах, резонансные частоты и структура поля колебаний
Прямоугольный объемный резонатор
Объемные прямоугольные резонаторы выполняют на основе прямоугольных волноводов замыканием проводящими плоскостями стенок волновода.
|
Резонансная частота колебаний Hmnp или Emnp прямоугольного резонатора (рис. |
||||||||||||||||
6.5) рассчитывается по формуле |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
m 2 |
n |
2 |
p |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
ε μ , ω0 = 2πf0 , |
||||||||||||
f0 |
= |
2 |
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
||
|
|
|
|||||||||||||||
|
|
|
|
a |
b |
|
l |
|
|
|
|
||||||
Y
b
Z λ |
a |
X |
- Н 101 |
В зависимости от ориентации системы координат основной тип колебаний может обозначаться как Н101 или Е110.
|
mπ 2 |
nπ 2 |
||||
k = |
|
|
|
+ |
|
|
|
b |
|||||
|
|
a |
|
|
||
Цилиндрический объемный резонатор
В цилиндрическом резонаторе могут возбуждаться колебания как электрического, так и магнитного типа.
Резонансная частота рассчитывается по формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
c |
|
ξ |
2 |
|
p 2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f0 |
mnp = |
|
|
|
|
mn |
+ |
|
|
εμ , |
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
πa |
|
l |
|
|
|||
|
Резонансная частота колебания типа H mnp |
рассчитывается по формуле |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
c |
|
|
η |
|
2 |
|
p 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f0 |
mnp = |
|
|
|
|
mn |
+ |
|
|
|
εμ . |
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
πa |
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

Е010
Коаксиальный резонатор
Коаксиальный резонатор работающий на колебаниях типа Tp , имеет компоненты
поля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pπ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Er = − jH0Zc |
r |
sin |
|
l |
|
z , |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
1 |
|
|
pπ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hϕ = H0 |
|
cos |
|
z , |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
l |
|
|
|||||
где H = |
|
Im |
|
, I |
|
– комплексная амплитуда тока внутреннего проводника в пучности. |
|||||||||||||||||||
2π |
m |
||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f |
|
= |
c |
|
p |
|
1 |
|
|
|
- резонансная частота |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
p |
2 l |
|
|
εμ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Кроме колебаний типа Tp , в коаксиальном резонаторе возможны колебания типа
Hmnp и Emnp .
Прямоугольный полосковый объемный резонатор представляет собой полосковый проводник, ограниченный со всех сторон прямоугольным экраном. По сравнению с обычными полосковыми резонаторами он имеет более высокую добротность. Анализ такой структуры можно проводить, рассматривая ее как волновод, частично заполненный диэлектриком. Резонатор имеет большие габариты, что затрудняет его использование. К образованию объемного полоскового резонатора может привести неудачный выбор размеров корпуса интегральной схемы, что является крайне нежелательным. Тщательная отработка конструкции позволяет предотвратить это.

14)Добротность объёмных резонаторов. Вычисление собственной и нагруженной добротности.
Добротность объемного резонатора
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q = 2πf0 |
W Э,М , |
|
|
|
|
(6.4) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pср.пот. |
|
|
|
|
|
|||||
|
|
|
|
ε a |
|
|
& |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
где |
W Э = ∫∫∫ |
|
|
E |
|
|
|
|
dv |
|
– |
|
среднее за период значение |
|
энергии электрического |
поля, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
запасенной в резонаторе, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
мa |
|
|
& |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
W М = |
∫∫∫ |
|
|
H |
|
|
|
dv |
– |
среднее за период значение энергии магнитного поля, запасенной в |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
резонаторе, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
= P |
Д |
+ |
М |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
(6.5) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ср.пот. |
|
|
ср.пот. |
ср.пот. , |
||||||||||
|
|
|
|
|
|
σ |
|
|
|
& |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
Pпотд . = ∫∫∫ |
|
|
E |
|
|
|
dv |
– |
мощность потерь, обусловленная проводимостью заполняющего |
||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
резонатор диэлектрика. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
м |
= |
|
Rs |
|
∫ |
|
|
|
|
2 |
|
– |
мощность потерь, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Pпот. |
|
|
|
|
|
|
|
& |
ds |
обусловленная неидеальной проводимостью |
|||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
H τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
стенок резонатора. Интегрирование ведется по поверхности стенок резонатора. |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
RS = |
|
ωμa |
|
|
|
– |
активное поверхностное сопротивление металла с проводимостью σ . |
||||||||||||||||||||||||||||||||||
|
|
|
2σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Потери в резонаторе приводят к уменьшению запасенной энергии по закону |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
ω0 |
t |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W (t ) = W e Q |
, |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
где W0 – энергия резонатора в начальный момент времени t0 . |
|
|
||||||||||||||||||||||||||||||||||||||||
|
Для пустого прямоугольного резонатора, работающего на колебании Н101, |
|
||||||||||||||||||||||||||||||||||||||||
добротность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0 μa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q = |
|
|
abl(a2 + l2) |
|
|
|
. |
(6.7) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2RS a3(l + 2b) + l3(a + |
2b) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Если резонатор заполнен диэлектриком с потерями, то результирующая |
|||||||||||||||||||||||||||||||||||||||||
добротность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q = |
|
|
|
1 |
|
|
|
|
, |
|
|
|
|
(6.8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 QM + tgδ |
|
|
|
|
|
||||||||
где QM – добротность резонатора, обладающего лишь потерями в металлических стенках |
||||||||||||||||||||||||||||||||||||||||||
Для цилиндрического: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Для колебаний типа H11P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
QH11 p = |
1 |
|
|
al |
|
|
|
|
|
|
|
|
|
. |
(6.11) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pλ |
0 |
2 |
|
|
|
η2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2a − l) |
|
|
+ l |
|
|
11 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2l |
|
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η11 −1 |
|
|
||||||||

Для колебаний типа H01P
|
|
QH01 p = |
1 |
|
|
|
|
|
|
|
|
al |
|
|
|
|
|
|
|
|
. |
|
(6.12) |
|||||||
|
|
|
|
|
(2a −l) |
Pλ0 |
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ l |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2l |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Для колебаний типа Е01P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
QE010 = |
1 |
|
|
|
lq |
, QE011 = |
1 |
|
|
la |
. |
(6.13) |
||||||||||||||||
|
|
l + a |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
l + a |
|
||||||||
|
Если резонатор заполнен диэлектриком с потерями, то результирующая добротность |
|||||||||||||||||||||||||||||
Q = |
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 QM + tg δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для коаксиального: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Добротность колебания типа Tp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2l ln |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Q = |
1 |
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
. |
|
|
|
|
|
(6.16) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
D |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
4ln |
|
|
|
+ l |
|
|
+ |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
d |
|
D |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
||||||||||
|
Если резонатор заполнен диэлектриком с потерями, то результирующая добротность |
|||||||||||||||||||||||||||||
Q = |
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 QM + tg δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

15)Затухание электромагнитных волн в линиях передачи.
Вреальной линии распространение волны сопровождается затуханием,
уменьшением передаваемой мощности. Это связано с потерями мощности в металлических проводниках линии, с затуханием волны в заполняющем диэлектрике, с излучением части мощности в окружающее пространство в линиях передачи открытого типа.
При наличии затухания вводится комплексное волновое число
γ& = β − jα ,
где β – коэффициент фазы; α – коэффициент затухания.
При этом зависимость векторов поля от координаты z принимает вид
e− jγz = e−αze− jβz |
|
|
|
|||||||
|
Мощность пропорциональна квадрату амплитуды поля и зависимость от координаты |
|||||||||
z определяется множителем e−2αz |
|
|
(z) = P (0)e−2αz . |
|||||||
Р |
|
|
=Р |
(z) − P (z + z) |
P |
|||||
пот.ср |
|
ср |
|
ср |
|
ср |
ср |
|||
P |
|
= |
lim |
|
Pср(z)−Pср(z+Δz) |
= − |
∂Pср |
откуда следует |
||
|
|
|
|
|||||||
пот.ср |
|
|
z→0 |
z |
∂z |
|
||||
|
|
|
|
|
|
|
|
|
||
α = Pпот.ср 2Рср
Если затухание распространяющейся волны невелико, то коэффициент ослабления
можно представить в виде суммы независимых коэффициентов
α = αm + αД + αΣ ,
(1.51)
где αm – коэффициент ослабления, обусловленный потерями в металлических
элементах линии; α – коэффициент ослабления, обусловленный потерями в
Д
диэлектрике, заполняющем линию; αΣ – коэффициент ослабления, обусловленный потерями энергии волны за счет излучения из линии.
В линиях закрытого типа αΣ = 0 .
Наличие отличных от нуля тангенциальных составляющих векторов E и H у поверхности металлических элементов означает, что вектор Пойнтинга имеет составляющую, направленную внутрь металла, то есть появляется поток мощности, направленный в металлические части линии, и в них происходят потери. Мощность потерь в проводниках вычисляется через граничные условия Леонтовича и на единицу длины линии она равна
|
|
|
1 |
|
|
R |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
& |
|
|
|
|
|
P |
|
= |
|
Rs ∫ |
∫ |
H τ |
|
de , |
|
|
|
2 |
|
|
|||||||
пот.ср |
|
L |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где L – |
контур поперечного сечения металлических элементов линии; R = |
ωμa |
– |
|||||||
|
|
|
|
|
|
|
|
s |
2σ |
|
активная часть поверхностного сопротивления проводника.
