П 1.4 Вычисление погрешностей арифметических операций

Рассмотрим правило вычисления погрешностей арифметических операций и функций по погрешности аргументов (без учета ошибок округления). При вычислении абсолютных погрешностей обычно используются формулы дифференцирования, в которых дифференциалы независимых переменных заменяются абсолютными погрешностями: .

Пусть X₁>0, X₂>0 – точные значения величин, и заданы предельные абсолютные погрешности и, т.е.,. Необходимо найти погрешность суммы.

Так как дифференциал , то. Отсюда следует, что.

Теперь предположим, что X₁>X₂, и найдем погрешность разности . Тогдаи. Поэтому.

Абсолютная погрешность суммы и разности двух приближенных чисел равна сумме абсолютных погрешностей слагаемых.

Это правило справедливо для произвольного числа слагаемых. Так если x₁, x₂, …, x_n имеют одну и ту же погрешность , то погрешность суммы этих слагаемых будет равна . Но реально погрешности могут иметь разные знаки и поэтому взаимно компенсировать друг друга. По правилу Чеботарева при погрешность суммы можно принять равной[20].

Для относительной погрешности суммы и разности двух чиселполучаем

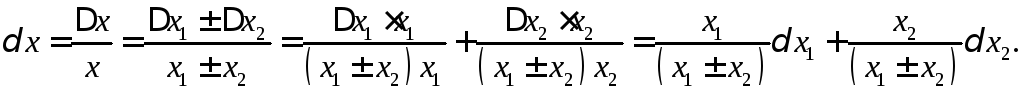
Для произвольного числа слагаемых

где , .

Пусть

Тогда

Поэтому

Аналогично при выполнении умножения и деления получаем погрешности (при тех же предположениях).

Найдем погрешность произведения :

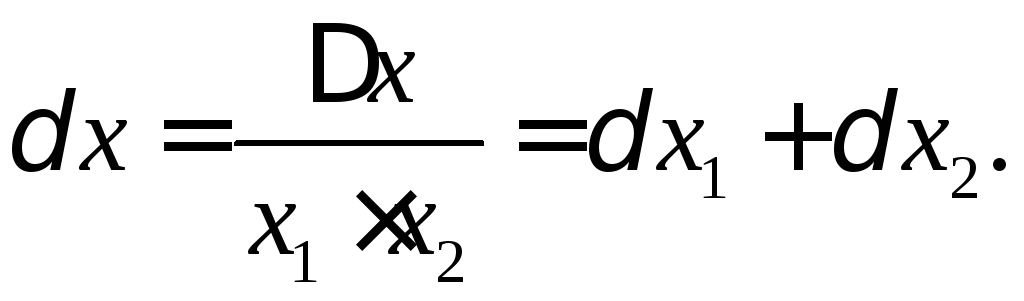
Найдем погрешность частного :

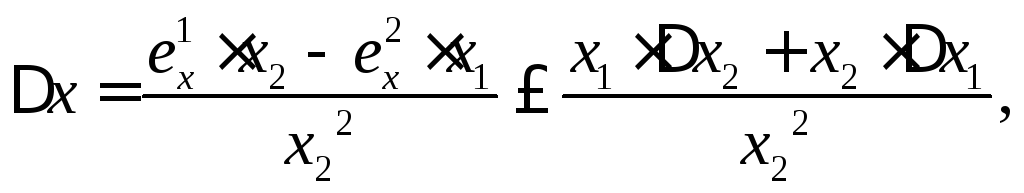
Следовательно, относительная погрешность произведения двух чисел равна сумме относительных погрешностей его сомножителей.

Аналогичное правило выполняется и для частного от деления двух чисел.

Также получаются формулы для погрешностей арифметических действий при вычислении функций многих переменных. Так, для имеем следующие формулы для погрешностей [20]:

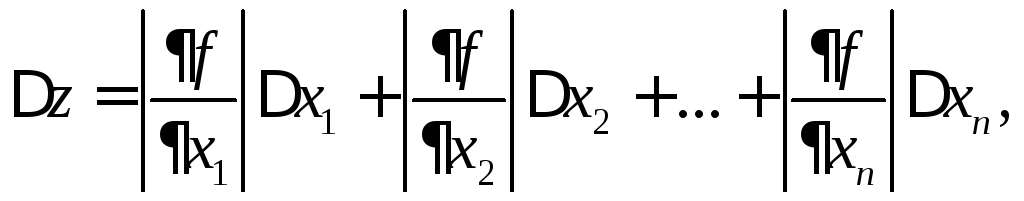
П 1.5 Оценка погрешности по способу границ

Способ границ применяется для оценки погрешности результата расчета по формуле, содержащей приближенные величины.

Пусть а – приближенное исходное данное, так что заданы его границы: . Нужно найти результату, зависящий от а и поэтому также приближенный: .

Найдем границы у, т.е. два таких числа и , что . Если результату увеличится с ростом а (например, площадь квадрата в зависимости от длины стороны), то, по определению границ, для любогои можно принять . Аналогично . Если у убывает с ростом а (например, давление воздуха с высотой), то и .

Для нахождения границ результата нужны два расчета по одному и тому же алгоритму с исходными данными и . Границы результата округляют так: – с недостатком, – с избытком. При этом в их записи сохранить все цифры до первой слева, отличие в которой и уже существенно.

Тогда значение у можем найти следующим образом:

.

А границы погрешности оцениваются:

.

Случай функции нескольких переменных.

Пусть a, b – исходные данные, известные приближенно:

, .

Если результат монотонно зависит от своих аргументов, то крайние его значения достигаются при некоторых комбинациях граничных значений исходных данных.

В общем случае следует провести 2 * 2 = 4 вычислений и выбрать из них пару: наибольший (ВГ(у)) и наименьший (НГ(у)) результаты. В случае трех исходных данных рассматривается 2³ = 8 расчетов и т.д. задача упрощается, если из ее постановки ясен характер зависимости: рост или убывание хотя бы по одному аргументу.

Пример 1. Произвести расчет по заданной формуле для приведенных исходных данных. Рассчитать границы, погрешность и значение результата.

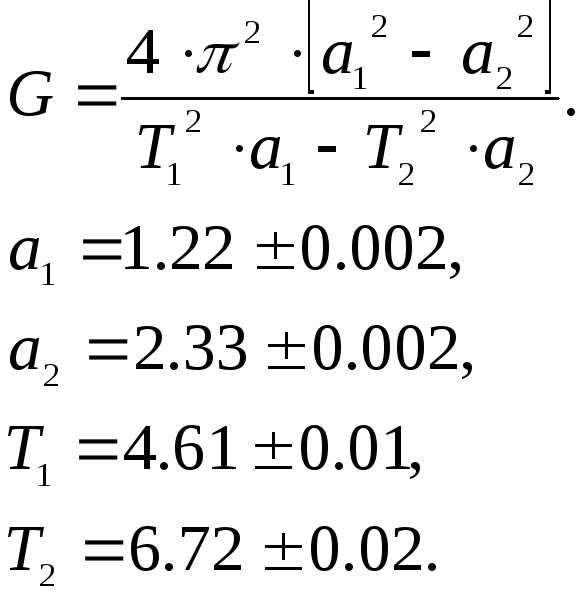
Проведем некоторые предварительные расчеты по длинной формуле. Выясним, как зависит функция G от а₁, а₂, Т₁, Т₂.

Зафиксируем а₁, а₂, Т₁ и вычислим

G(1.22, 2.33, 4.61, 6.74) =1.946536,

G(1.22, 2.33, 4.61, 6.70) = 1.977531.

Видно, что с возрастанием T₂ убывает функция G.

Зафиксируем ,,и вычислим

G(1.22, 2.33, 4.62, 6.72) = 1.964724,

G(1.22, 2.33, 4.60, 6.72) = 1.959158.

Видно, что G возрастает с ростом T₁.

Зафиксируем ,,и вычислим

G(1.22, 2.332, 4.61, 6.72) = 1.964339,

G(1.22, 2.328, 4.61, 6.72) = 1.959528.

Видно, что G возрастает с ростом a₂.

Зафиксируем ,,и вычислим

G(1.222, 2.33, 4.61, 6.72) = 1.960553,

G(1.218, 2.33, 4.61, 6.72) = 1.963309.

Видно, что с возрастанием a₁ убывает функция G.

Найдем границы G:

ВГ(G) = G(НГ(а₁), ВГ(а₂), ВГ(Т₁), НГ(Т₂)) = 1.984156,

НГ(G) = G(ВГ(а₁), НГ(а₂), НГ(Т₁), ВГ(Т₂)) =1.940027.

Видно, что различие в третьей цифре уже существенно.

Округляем НГ – с недостатком, ВГ – с избытком.

ВГ(G) = 1.99,

НГ(G) =1.94.

Тогда ,.