Лабораторная работа № 14

Цель: изучить итерационный степенной метод нахождения наибольшего по модулю собственного значения и соответствующего собственного вектора.

Задание

1. Разработайте класс «Частичная проблема нахождения собственных значений» («PartialProblem»), который наследуется от класса «Итерационные методы нахождения собственных значений» («IterationMethodsE»). В данном классе реализуйте итерационный метод («iterationMethod») нахождения наибольшего по модулю собственного значения и соответствующего собственного вектора.

Для реализации метода используйте объекты матричных классов «SquareMatrix» и «Vector». Доступ к элементам осуществляйте с помощью методов getElement и setElement, реализованных в данных классах. Для операции умножения матрицы на вектор используйте метод, реализованный в классе «SquareMatrix».

2. Методом итераций определите наибольшее по модулю собственное значение и соответствующий ему собственный вектор матрицы () в соответствии с вариантом.

3. Решите ту же задачу, используя пакет для математических вычислений.

4. Сравните результат выполнения п. 2 с решением, полученным в п. 3.

Варианты заданий

№ 1	№ 2
№ 3	№ 4
№ 5	№ 6
№ 7	№ 8
№ 9	№ 10
№ 11	№ 12
№ 13	№ 14
№ 15	№ 16

П 4.3 qr-алгоритм для нахождения собственных значений матрицы

При решении полной проблемы собственных значений для несимметричных матриц эффективным является подход, основанный на приведении матриц к подобным, имеющим треугольный или квазитреугольный вид. Одним из наиболее распространенных методов этого класса является QR-алгоритм, позволяющий находить как вещественные, так и комплексные собственные значения.

Основная идея QR-алгоритма состоит в разложении матрицы А в произведение ортогональной и верхней треугольной матрицы. Предполагаем, что все собственные значения матрицы А различны по абсолютной величине и .

Процедура QR-разложения, рассмотренная в П 2.2, многократно используется в R-алгоритме вычисления собственных значений.

Осуществляя поочередно факторизацию и перестановку сомножителей, получаем последовательность матриц [20]

, , , (1)

где  ортогональная матрица,  верхняя треугольная матрица, .

Таким образом, каждая итерация реализуется в два этапа. На первом этапе осуществляется разложение матрицы в произведение ортогональнойи верхней треугольнойматриц, а на втором – полученные матрицы перемножаются в обратном порядке.

Из равенства (1) получаем, отсюда . Получаем, что все матрицы подобны между собой и подобны исходной матрице А.

При отсутствии у матрицы кратных собственных значений последовательность сходится к верхней треугольной матрице (в случае, когда все собственные значения вещественны) или к верхней квазитреугольной матрице (если имеются комплексно-сопряженные пары собственных значений).

Таким образом, каждому вещественному собственному значению будет соответствовать столбец со стремящимися к нулю поддиагональными элементами и в качестве критерия сходимости итерационного процесса для таких собственных значений можно использовать следующее равенство:

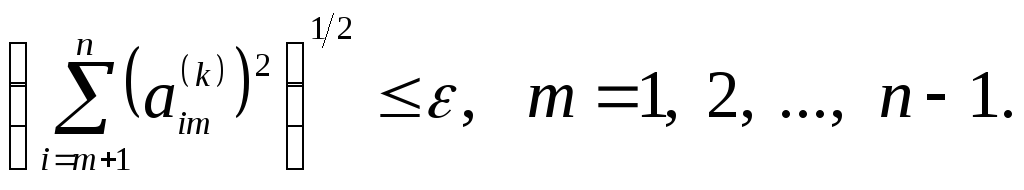
При этом соответствующее собственное значение принимается равным диагональному элементу данного столбца.

Каждой комплексно-сопряженной паре соответствует диагональный блок размерностью 2х2. Принципиально то, что элементы этих блоков изменяются от итерации к итерации без видимой закономерности, в то время как комплексно-сопряженные собственные значения, определяемые каждым блоком, имеют тенденцию к сходимости. Это обстоятельство необходимо учитывать при формировании критерия выхода из итерационного процесса. Если в ходе итераций прослеживается комплексно-сопряженная пара собственных значений, соответствующая блоку, образуемому элементами j-го и j+1-го столбцов, то, несмотря на значительное изменение в ходе итераций самих этих элементов, собственные значения, соответствующие данному блоку и определяемые из решения квадратного уравнения

,

начиная с некоторого k отличаются незначительно.

Для практического QR-алгоритма нет завершенной теории сходимости. На практике алгоритм работает всегда или почти всегда [5].

Пример 1. Используя QR-алгоритм, найти собственные значения матрицы 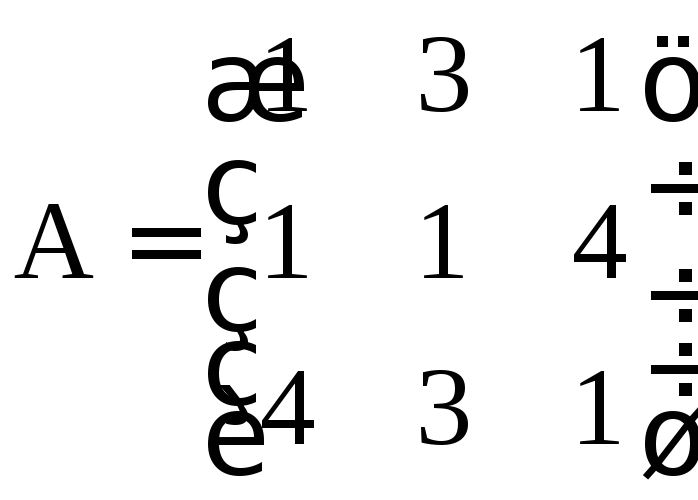с точностью .

Решение:

Выберем вектор согласно формуле (5), рассмотренной в П 2.2:

,

где, .

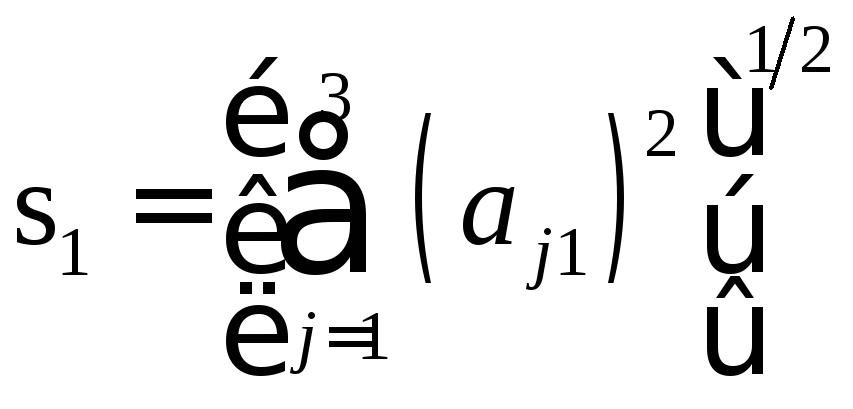Тогда .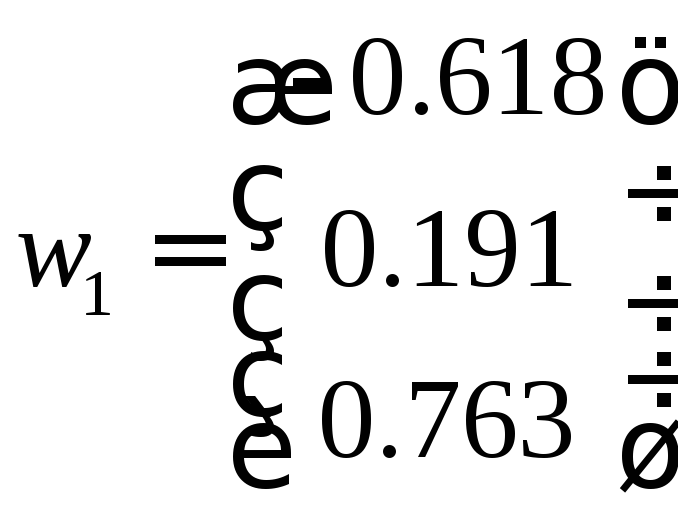

Построим матрицу согласно формуле (6), рассмотренной в П 2.2:

,

.

Выберем вектор :

,

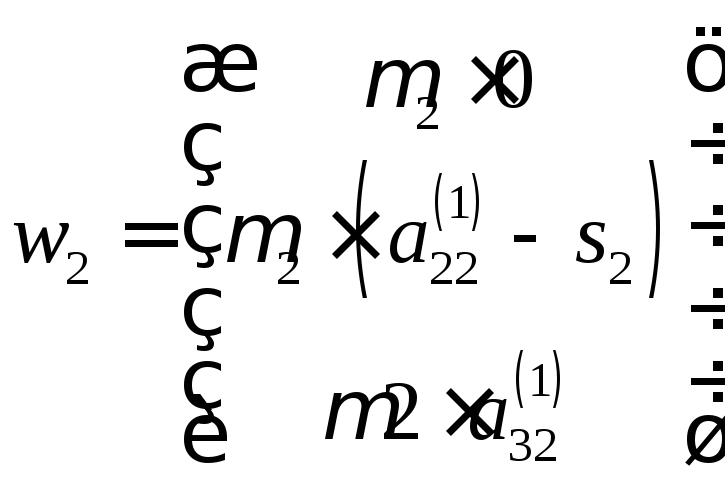где ,.

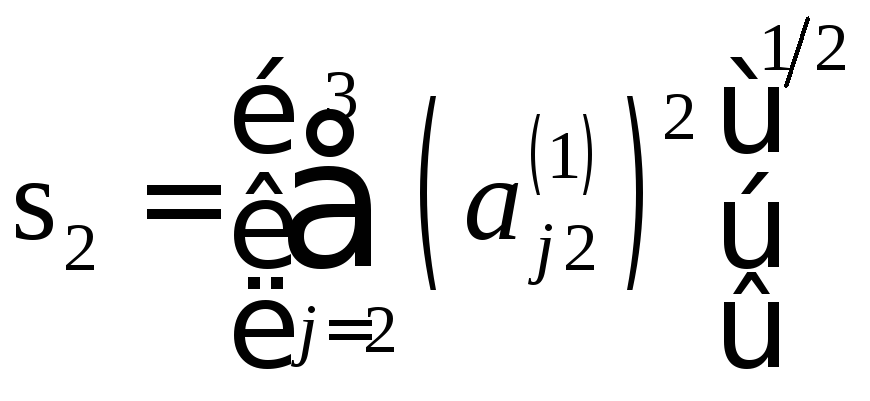Тогда .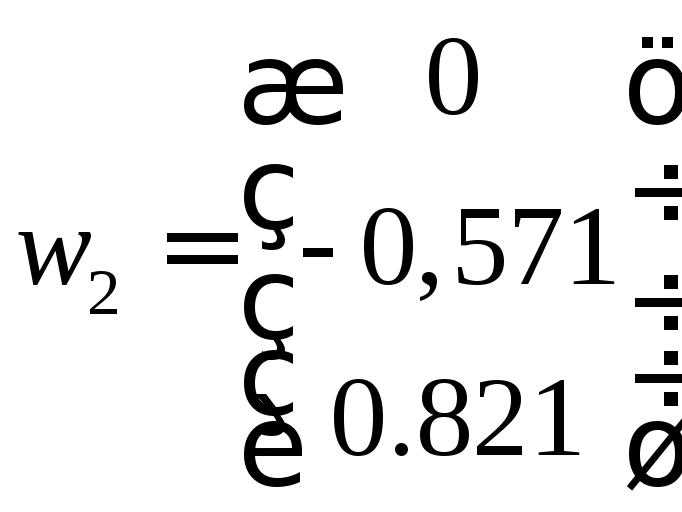

Построим матрицу по формуле (6) из П 2.2:

,

.

Построим матрицу Q согласно формуле (8), описанной в П 2.2:

,

.

Убедимся, что матрица Q – ортогональна.

.

Построим верхнюю треугольную матрицу R по формуле (7) из П 2.2:

,

.

После первой итерации матрица А вычисляется по формуле и имеет вид:

.

Первая итерация завершена. Поддиагональные элементы матрицы достаточно велики, поэтому итерационный процесс необходимо продолжать.

Продолжая итерационный процесс, получим соответственно на 6-й и 7-й итерациях следующие матрицы:

,

.

Видно, что поддиагональные элементы первого столбца становятся достаточно малыми, и, следовательно, диагональный элемент может быть принят в качестве собственного значения. В то же время отчетливо прослеживается комплексно-сопряженная пара собственных значений, соответствующая блоку, образуемому элементами второго и третьего столбцов. Собственные значения, соответствующие данному блоку, определяются из решения квадратного уравнения

.

Таким образом, окончательное решение задачи можно записать в виде: ,,.