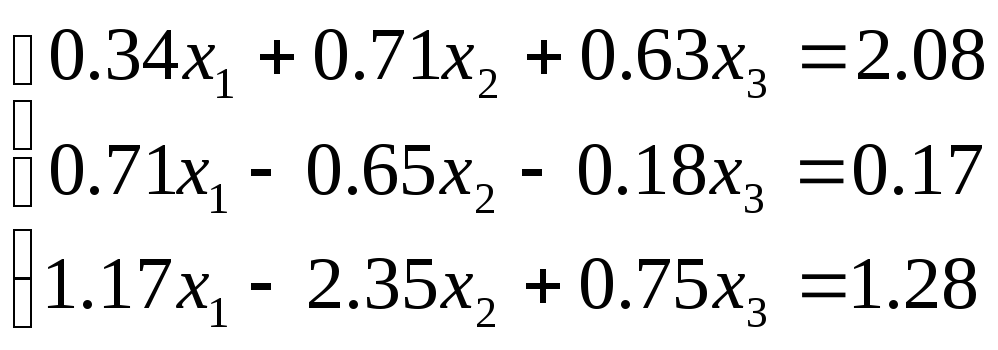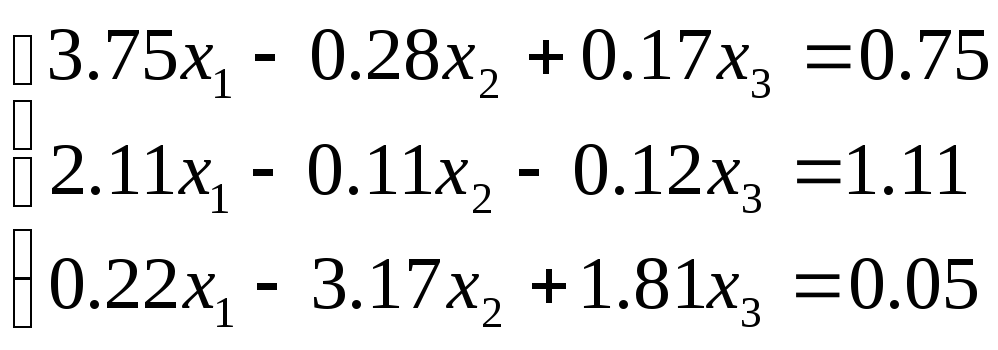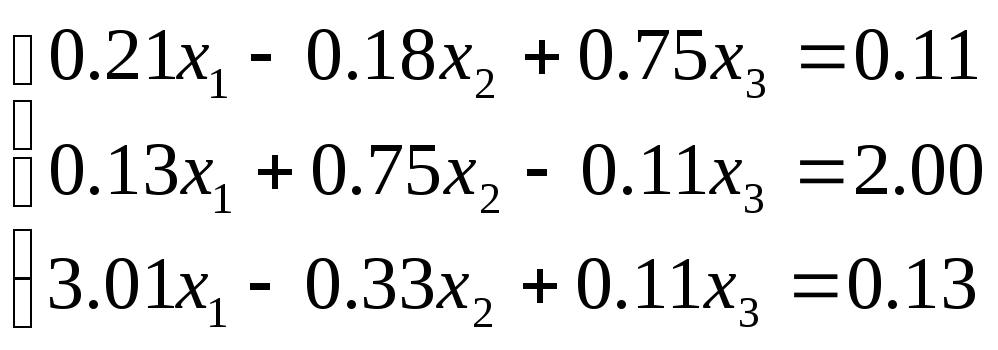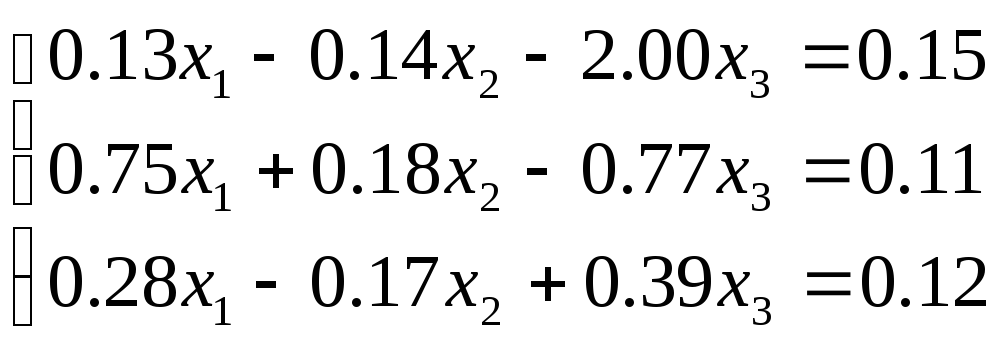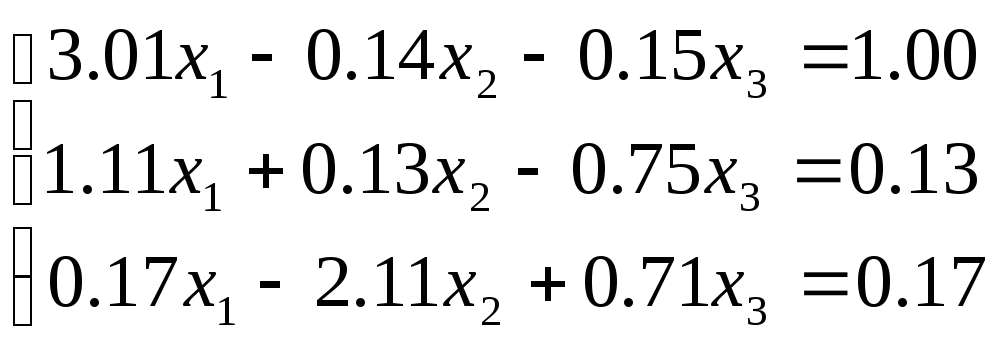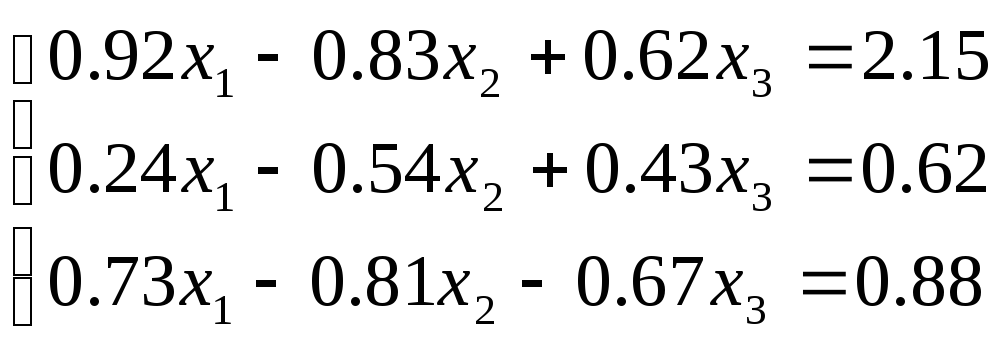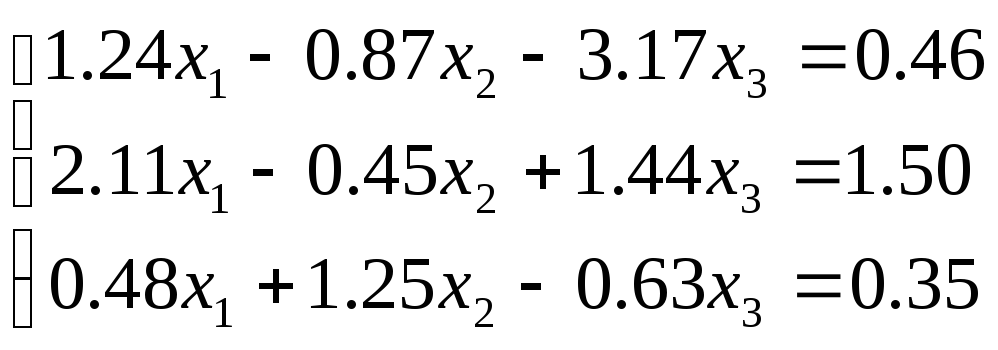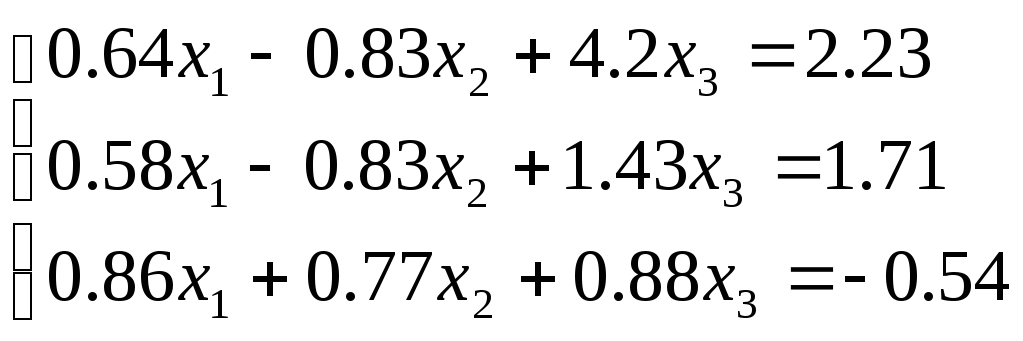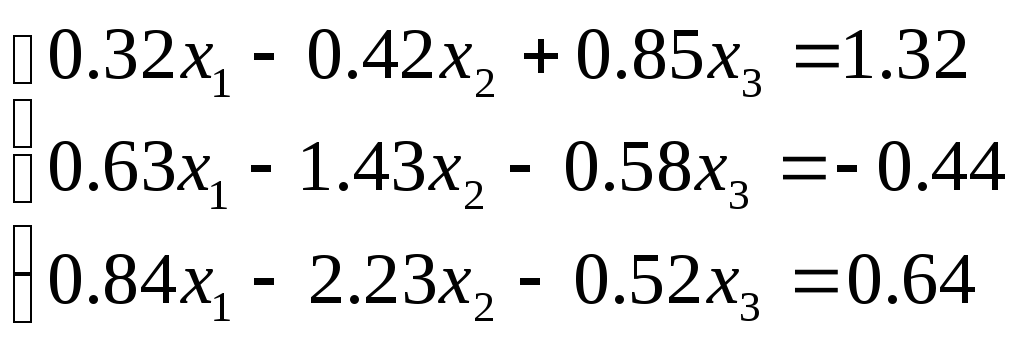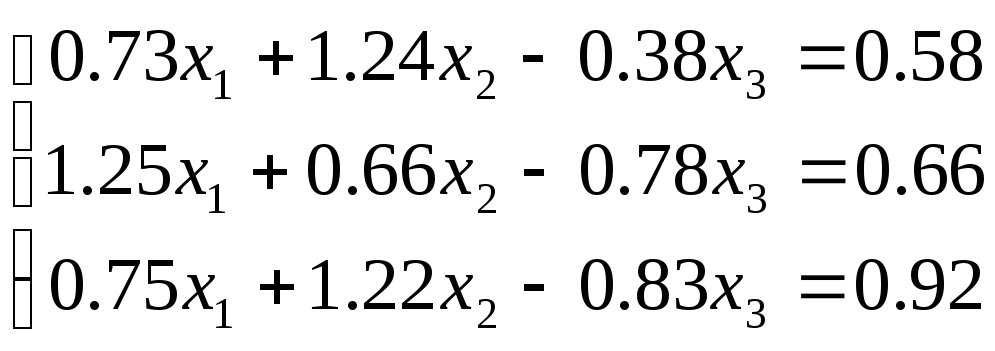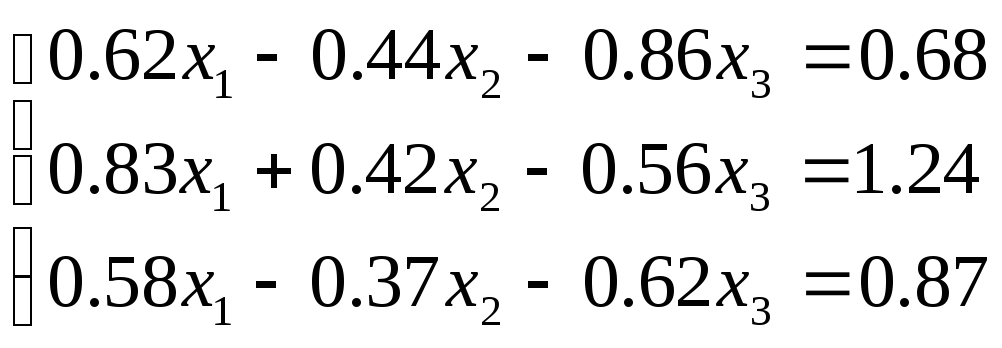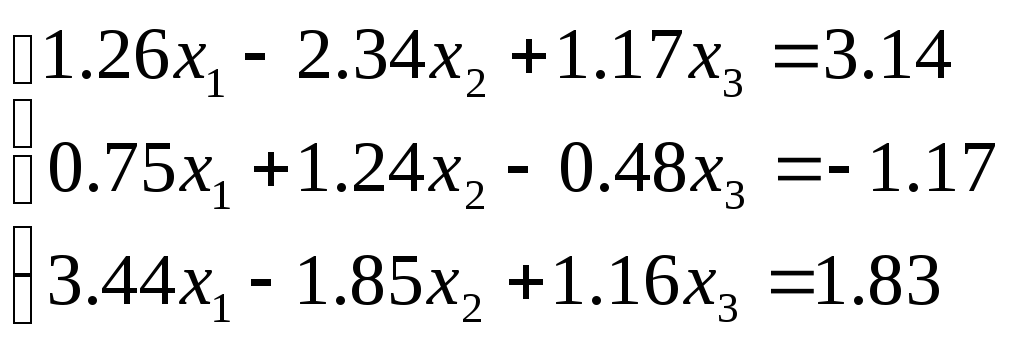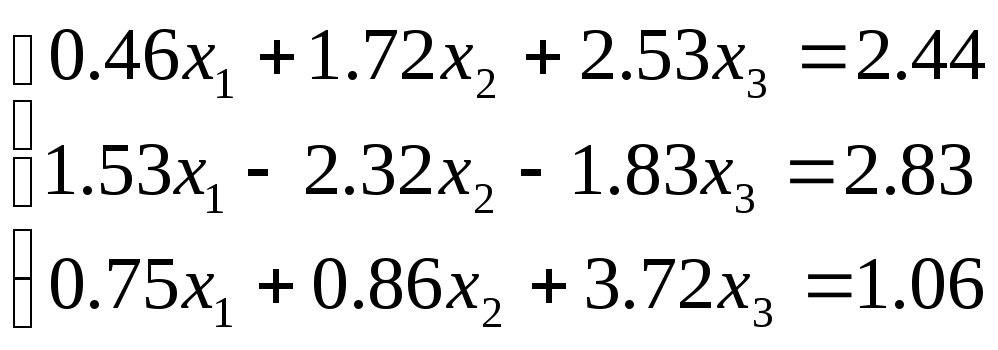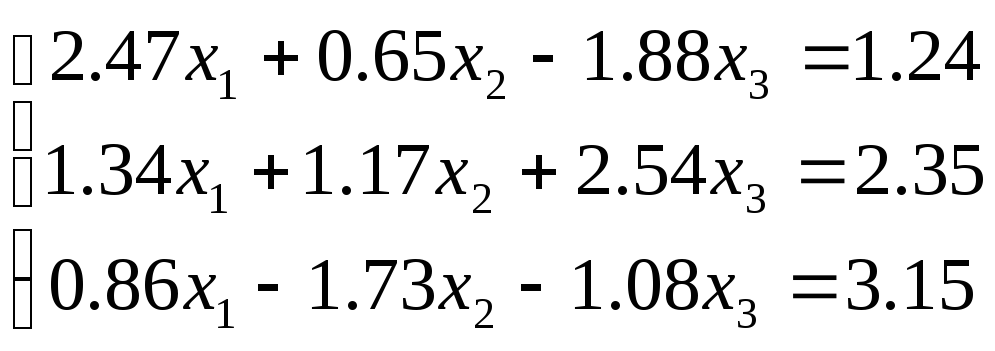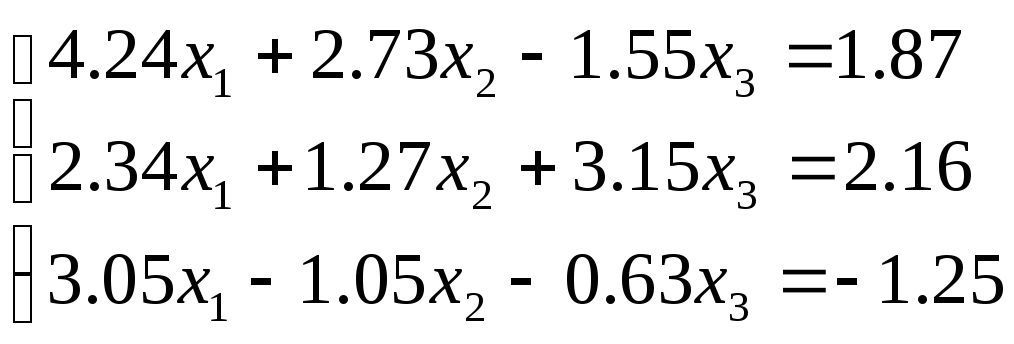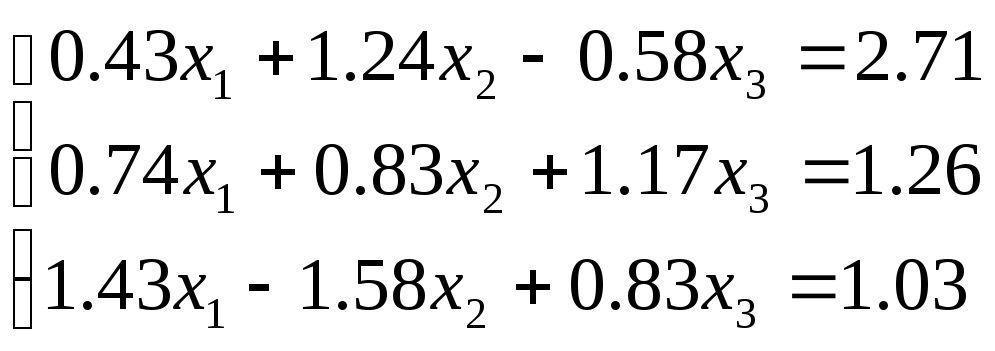- •Л.В. Маркова, е.А. Корчевская,
- •С о д е р ж а н и е
- •П р е д и с л о в и е
- •Глава 1 Элементы теории погрешностей п 1.1 Источники погрешностей
- •П 1.2 Вычисление абсолютной и относительной погрешностей
- •П 1.3 Округление чисел
- •П 1.4 Вычисление погрешностей арифметических операций
- •П 1.5 Оценка погрешности по способу границ
- •Лабораторная работа № 1
- •Задание
- •Глава 2 объектно-ориентированный подход к программированию методов линейной алгебры
- •П 2.1 Создание матричной иерархии классов
- •Лабораторная работа № 2
- •Задание
- •П 2.2 Создание иерархии классов вычислительных методов алгебры
- •Лабораторная работа № 3
- •Задание
- •Глава 3 решение систем линейных алгебраических уравнений
- •П 3.1 Метод Гаусса решения систем линейных алгебраических уравнений
- •Лабораторная работа № 4
- •Задание
- •П 3.2 Метод Гаусса с выбором главного элемента для решения систем линейных алгебраических уравнений
- •Лабораторная работа № 5
- •Задание
- •П 3.3 Решение системы линейных алгебраических уравнений методом Жордана-Гаусса
- •Лабораторная работа № 6
- •Задание
- •П 3.4 Метод квадратного корня для решения систем линейных алгебраических уравнений
- •Лабораторная работа № 7
- •Задание
- •П 3.5 Вычисления определителя и нахождения обратной матрицы
- •Лабораторная работа № 8
- •Задание
- •П 3.6 Решение системы линейных алгебраических уравнений методом прогонки
- •Лабораторная работа № 9
- •Задание
- •П 3.7 Метод простых итераций решения систем линейных алгебраических уравнений
- •Лабораторная работа № 10
- •Задание
- •П 3.8 Метод Зейделя решения систем линейных алгебраических уравнений
- •Лабораторная работа № 11
- •Задание
- •П 3.9 Итерационные методы вариационного типа решения систем линейных алгебраических уравнений
- •Лабораторная работа № 12
- •Задание
- •Глава 4 вычисление собственных значений и собственных векторов матриц
- •П 4.1 Метод Данилевского для нахождения собственных значений и собственных векторов
- •Лабораторная работа № 13
- •Задание
- •П 4.2 Итерационный степенной метод нахождения наибольшего по модулю собственного значения и соответствующего собственного вектора
- •Лабораторная работа № 14
- •Задание
- •П 4.3 qr-алгоритм для нахождения собственных значений матрицы
- •Лабораторная работа № 15
- •Задание
- •П 4.4 Метод Якоби для нахождения собственных значений и собственных векторов
- •Лабораторная работа № 16
- •Задание
- •П р и л о ж е н и я Приложение 1 Основные сведения о матрицах
- •Функции MathCad
- •Л и т е р а т у р а
- •Красоткина вычислительные методы алгебры. Практикум
- •2 10038, Г. Витебск, Московский проспект, 33.
Лабораторная работа № 5
Цель: изучить метод Гаусса с выбором главного элемента для решения систем линейных алгебраических уравнений.
Задание
1. Реализуйте в классе «DirectMethodsFactorization» метод Гаусса с выбором главного элемента («gaussChooseElement»). Для реализации метода используйте объекты и методы матричных классов «SquareMatrix», «Vector», «AugmentMatrix» и «SwapMatrix». Продумайте и реализуйте методы работы с матрицей класса «SwapMatrix». Возможная структура класса «SwapMatrix» приведена в примере 2. Для эффективной реализации метода все необходимые матричные операции производите над объектом класса «AugmentMatrix», описанным в примере 2.
2. Решите систему
линейных алгебраических уравнений
методом Гаусса с выбором главного
элемента (![]() )
в соответствии с вариантом.
)
в соответствии с вариантом.
3. Решите ту же задачу, используя пакет для математических вычислений.
4. Сравните результат выполнения п. 2 с решением, полученным в п. 3
Варианты заданий
|
№ 1
|
№ 2
|
|
№ 3
|
№ 4
|
|
№ 5
|
№ 6
|
|
№ 7
|
№ 8
|
|
№ 9
|
№ 10
|
|
№ 11
|
№ 12
|
|
№ 13
|
№ 14
|
|
№ 15
|
№ 16
|
П 3.3 Решение системы линейных алгебраических уравнений методом Жордана-Гаусса
Рассмотрим метод Жордана-Гаусса.
Имеем систему линейных алгебраических уравнений:
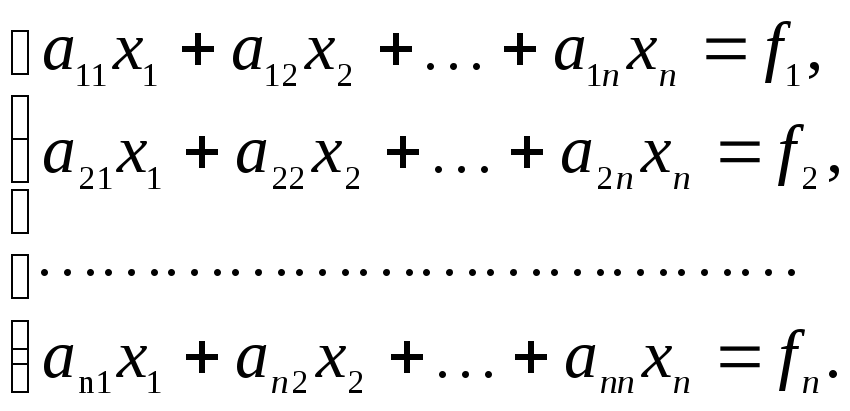 (1)
(1)
или в матричном виде AX = f. (2)
Суть метода Жордана-Гаусса состоит в том, чтобы привести матрицу А к единичному виду, тогда вектор решения будет совпадать со столбцом свободных членов. Алгоритмически метод Жордана-Гаусса объединяет прямой и обратный ход метода Гаусса [3].
Первый шаг метода
Жордана-Гаусса аналогичен первому шагу
метода Гаусса, т.е. первое уравнение
необходимо разделить на
![]() –коэффициент
при неизвестном
–коэффициент
при неизвестном
![]() и исключить это неизвестное –
и исключить это неизвестное –![]() из остальных уравнений системы. На
втором шаге необходимо исключить
неизвестное
из остальных уравнений системы. На
втором шаге необходимо исключить
неизвестное![]() из всех
уравнений системы (в том числе из первого)
кроме второго. На третьем шаге оставляем
неизвестное
из всех
уравнений системы (в том числе из первого)
кроме второго. На третьем шаге оставляем
неизвестное
![]() только в
третьем уравнении и т.д. Окончательно
получаем систему вида
только в
третьем уравнении и т.д. Окончательно
получаем систему вида
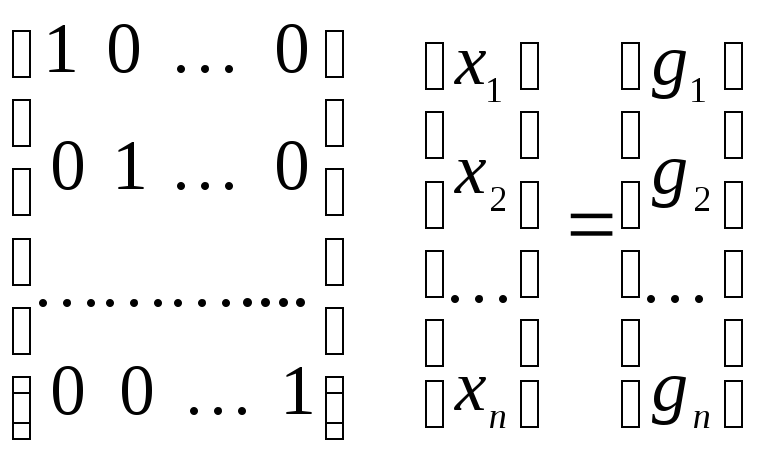 .
.
Столбец свободных членов в последней расширенной матрице и есть решение системы (1).
Пример 1. Решить с помощью метода Жордана-Гаусса систему уравнений:
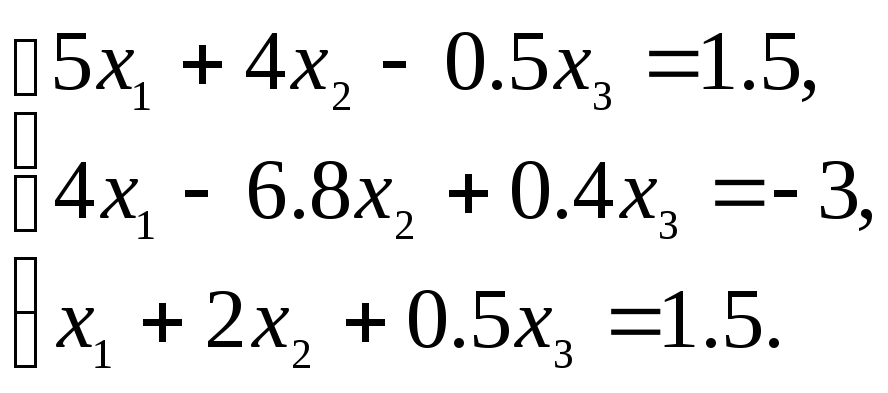
Решение:
Разделим первое уравнение на 3, получим следующую систему:
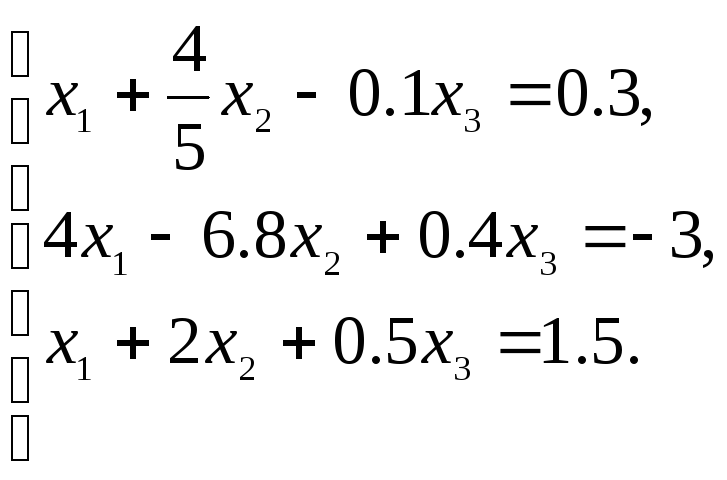
Сложим первое уравнение со вторым и третьим, умножив соответственно на –4 и –1, получим систему:
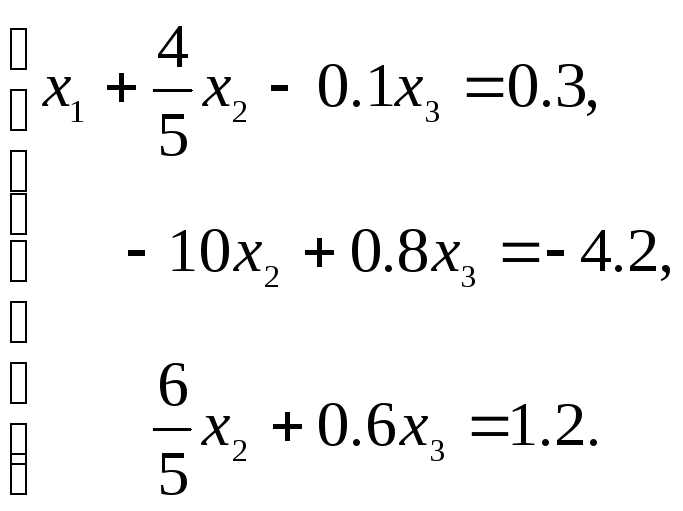
Разделим второе уравнение на –10, получим следующую систему:
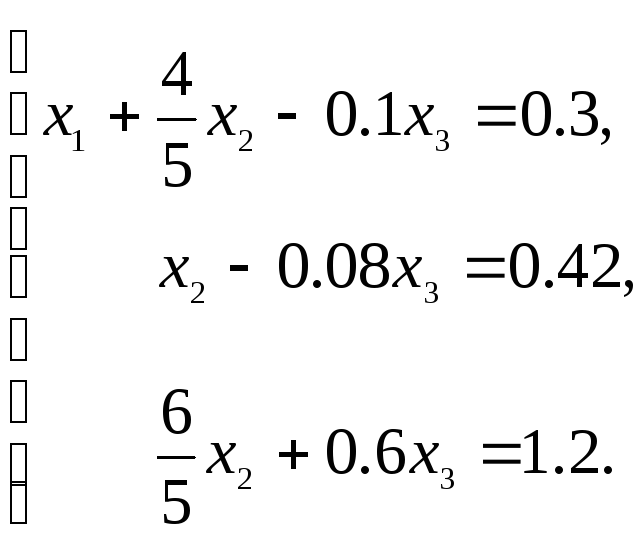
Сложим второе уравнение с первым и третьим, умножив соответственно на –4/5 и –6/5, получим:
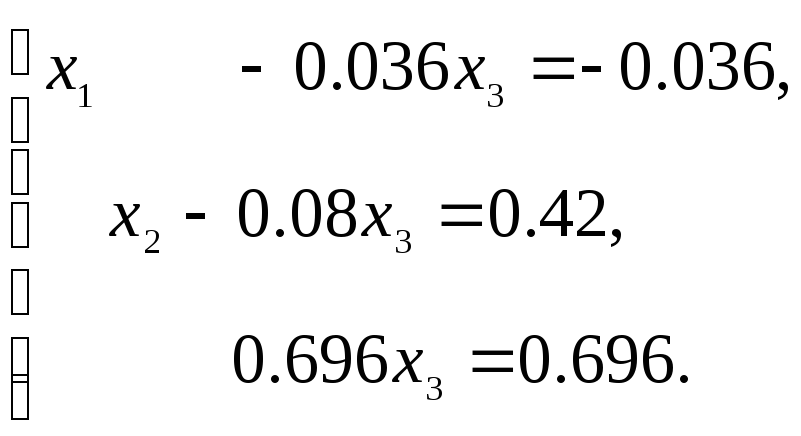
Разделим третье уравнение на 0.696, получим следующую систему:
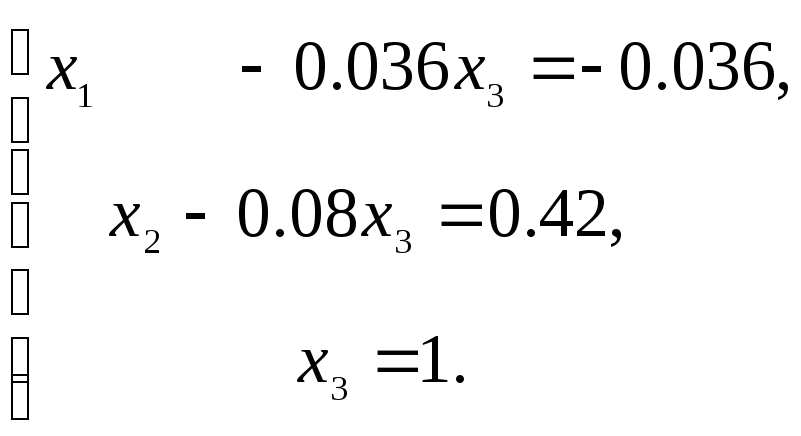
Сложим третье уравнение с первым и вторым, умножив его на 0.036 и 0.08, получим:
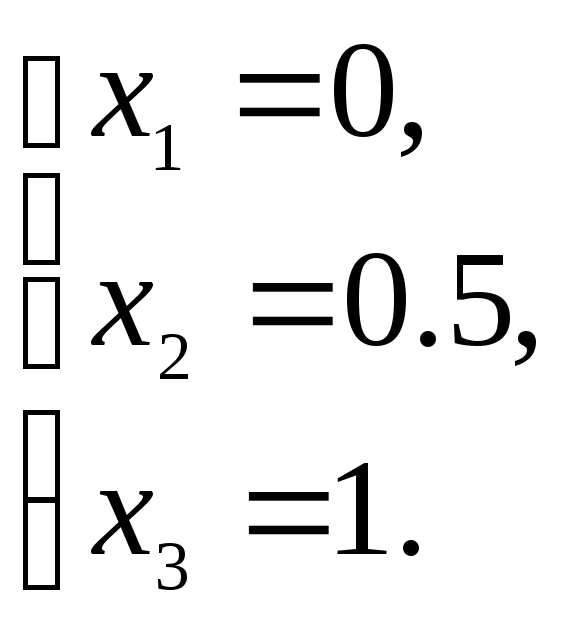
Рассмотрим метод Жордана-Гаусса на основе факторизации.
На первом шаге
исключения матрица системы (2) приводится
к виду
 .
.
Этот шаг эквивалентен
умножению матрицы системы (2) слева на
элементарную нижнюю треугольную
матрицу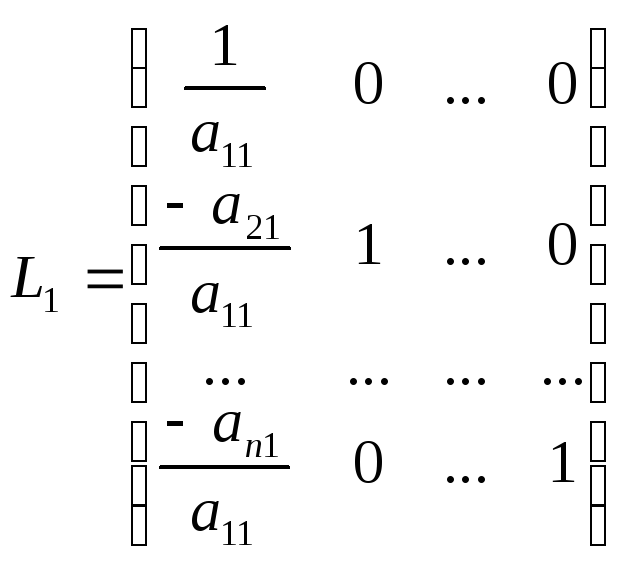 .
.
В результате имеем
систему
![]() .
(3)
.
(3)
На втором шаге
исключения матрица системы (3) приводится
к виду
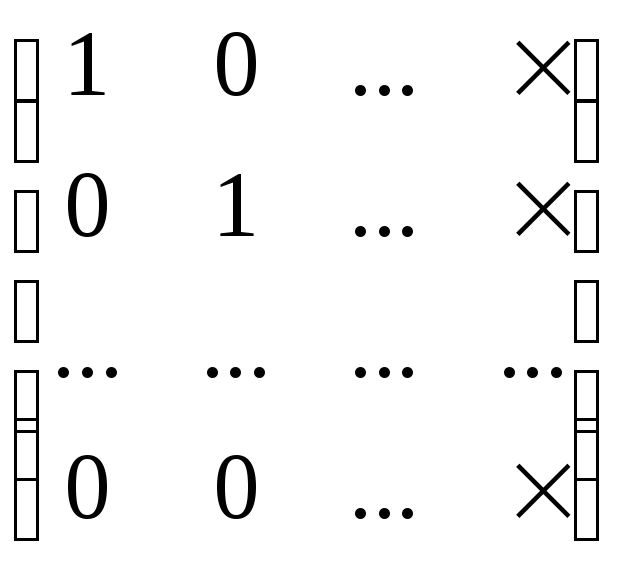 .
.
Для этого необходимо
умножить матрицу системы (3) слева на
элементарную нижнюю треугольную матрицу
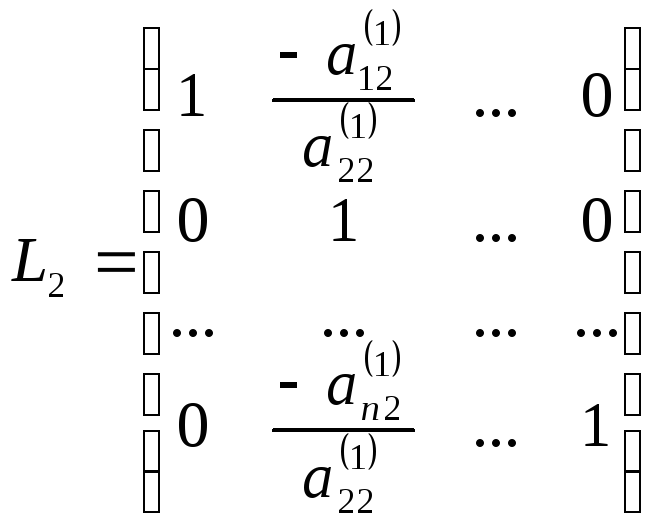 .
.
В результате
получим систему
![]() . (4)
. (4)
Продолжая этот процесс, в итоге приходим к системе
![]() , (5)
, (5)
где на к-ом
шаге исключения элементарная нижняя
треугольная матрица
![]() имеет вид
имеет вид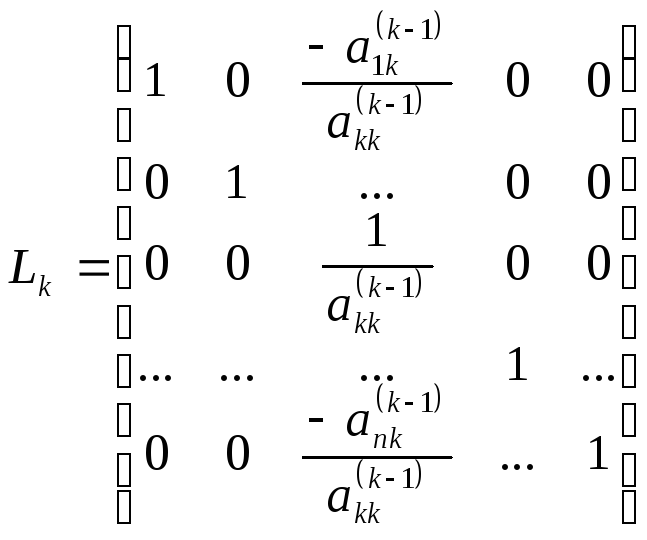 .
.
Исходя из того,
что ![]() ,перепишем систему
(5) в виде
,перепишем систему
(5) в виде
![]() .
(6)
.
(6)
Таким образом, правая часть системы (6) представляет собой искомый вектор решения.
Пример 2. Решить с помощью метода Жордана-Гаусса на основе факторизации систему уравнений:
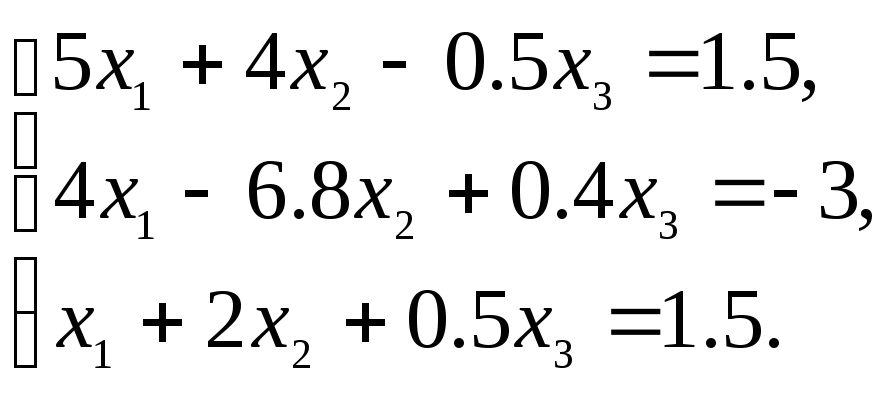
Решение:
Перепишем систему в матричном виде
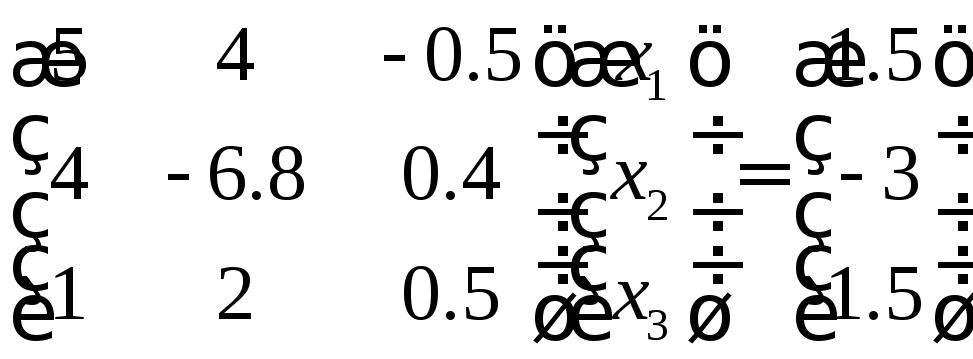 .
.
Применим первый
шаг исключения, для этого умножим матрицу
системы слева на матрицу
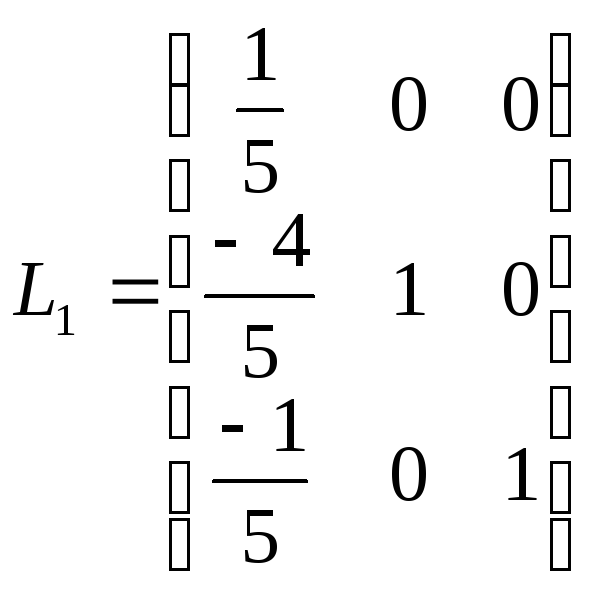 .
.
Получим систему
![]() или в развернутом виде
или в развернутом виде
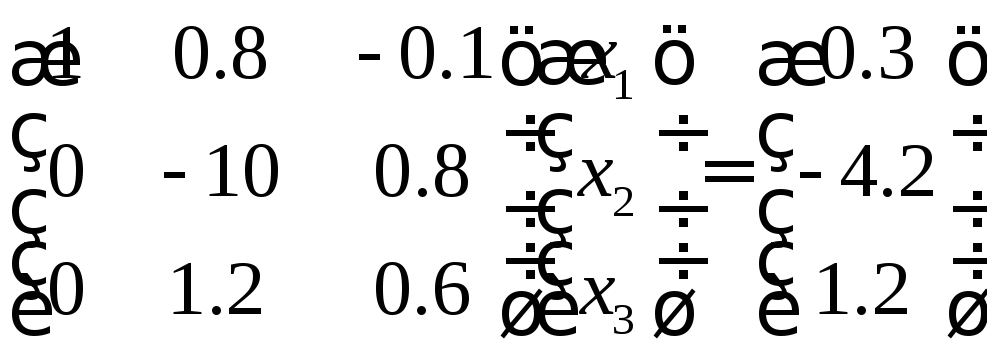 .
.
Далее применим
второй шаг исключения, для этого матрицу
системы, полученной на предыдущем шаге,
умножим слева на матрицу
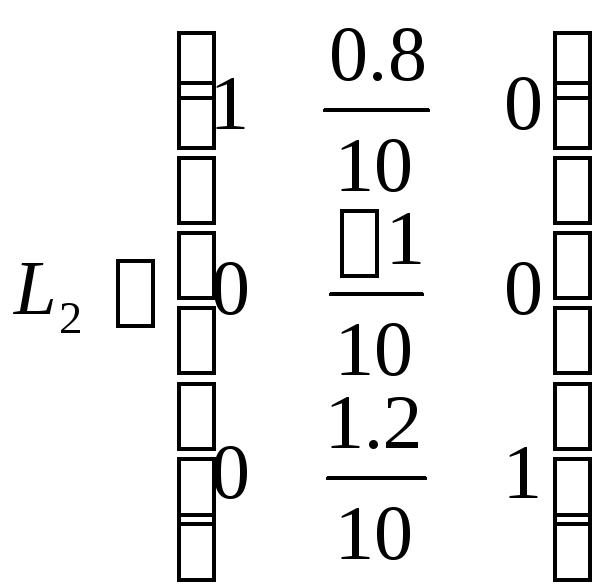 .
.
Имеем систему
![]() или
или
 .
.
На заключительном
этапе имеем систему
![]() ,
где матрица
,
где матрица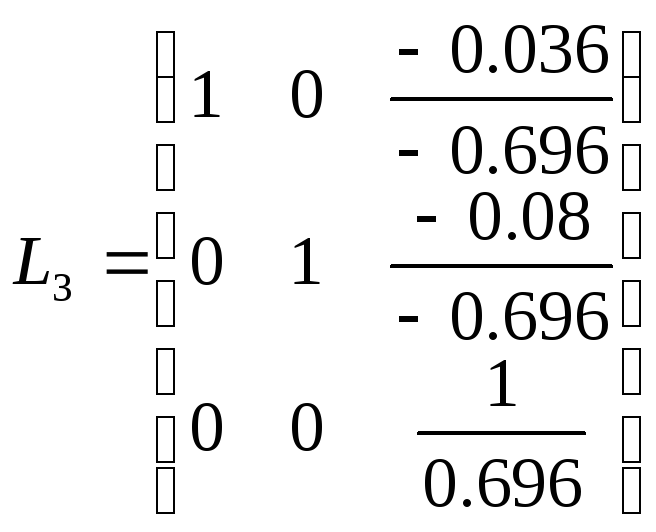 .
.
В результате
получим систему
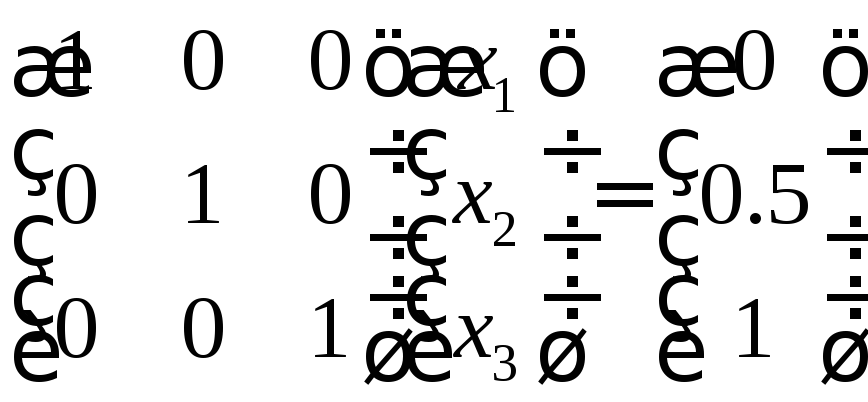 .
.
Отсюда следует,
что искомый вектор найден
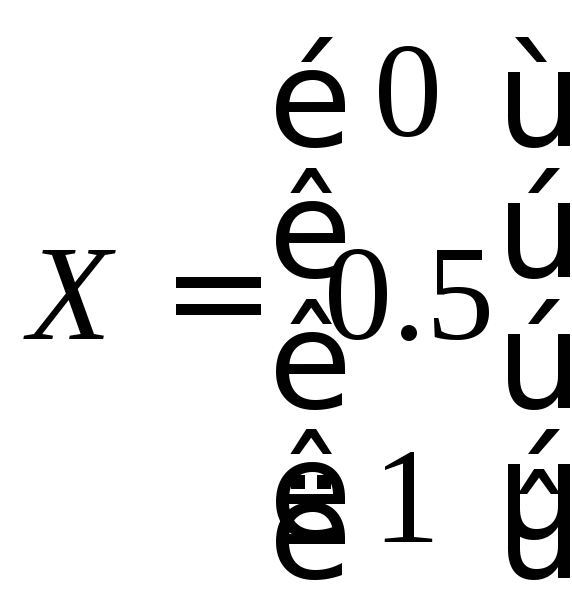 .
.