Избыточность кода Хаффмена

Из теоремы 8.1 следует, что для построенных по алгоритму Хаффмана кодов средняя длина кодовых слов удовлетворяет неравенству

, (8.16)

где — энтропия ансамбля.

Разность называется избыточностью неравномерного кода. При кодировании с избыточностью на каждое сообщение затрачивается на бит больше, чем в принципе можно было бы потратить, если использовать теоретичес­ки наилучший (возможно, нереализуемый) способ кодирования.

Итак, из (8.16) следует, что для кода Хаффмана избыточность г < 1. Хоте­лось бы получить более точную оценку средней длины кодовых слов. Гораздо бо­лее точную оценку избыточности получил Р. Галлагер, наложив ограничение на максимальную из вероятностей сообщений.

Теорема 8.3. Пусть — наибольшая из вероятностей сообщений конечно­го дискретного ансамбля. Тогда избыточность кода Хаффмана для этого ансамбля удовлетворяет неравенствам:

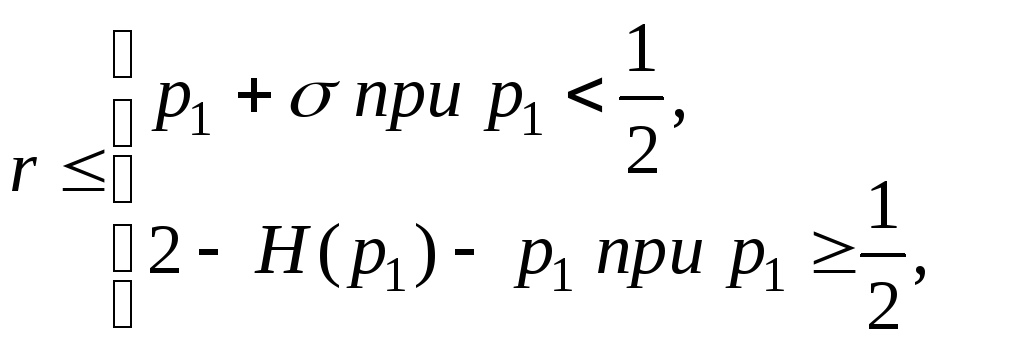
где — энтропия двоичного ансамбля; .

8.3.4. Код Шеннона-Фано

Алгоритм Шеннона-Фано заключается в следующем.

1. Символы алфавита источника записываются в порядке не возрас­тающих вероятностей.

2. Затем они разделяются на две части так, чтобы суммы вероятностей символов, входящих в каждую из таких частей, были примерно одинаковыми. Всем символам первой части приписывается в качестве первого символа комбинации неравномерного кода ноль, а символам второй части — единица.

3. Затем каждая из этих частей (если она содержит более одного символа) делится в свою очередь на две, по возможности равновероятные части и к ним применяется то же самое правило кодирования.

4. Этот процесс повторя­ется до тех пор, пока в каждой из полученных частей не останется по одному сообщению.

Пример. Пусть алфавит А источника состоит из 8 символов А, Б, В, Г, Д, Е, Ж, З с ве­роятностями р(А) = 0,6; р(Б) = 0,2; р(В) = 0,1; р(Г) = 0,04; р(Д)=0,025; р(Е) = 0,015, р(Ж)=0,01; р(З) = 0,01. Про­цедура построения неравномерного кода Шеннона-Фано задается в таблице 8.9.

Таблица 8.9. Про­цедура построения неравномерного кода Шеннона-Фано

Буква	рi	I	II	III	IV	V	VI	Kод	mi	mi  pi
А	0.6	1						1	1	0.6
Б	0.2	0	1	1				011	3	0.6
В	0.1			0				010	3	0.3
Г	0.04		0	1				001	3	0.12
Д	0.025			0	1			0001	4	0.1
Е	0.015				0	1		00001	5	0.075
Ж	0.01					0	1	000001	6	0.06
З	0.01						0	000000	6	0.06

На первом этапе производится деление на два множества А, и Б, В, Г, Д, Е, Ж, З, так как вероятность р(А)=0,6 и сумма вероятностей

примерно одинаковы. При этом символу А присваивается «1», а всем остальным Б, В, Г, Д, Е, Ж, З присваивается «0».

На втором этапе производится деление второго множества на два множества Б, В, и Г, Д, Е, Ж, З. Множеству Б, В присваивается «1», а множеству Г, Д, Е, Ж, З присваивается «0».

Hа третьем этапе производится деление множества Б, В, на два множества (уже символа) Б и В. Символу Б присваивается «1», а символу В присваивается «0». Множество Г, Д, Е, Ж, З делится на множества Г и Д, Е, Ж, З. Символу Г присваивается «1», а множеству Д, Е, Ж, З присваивается «0».

На четвёртом этапе производится деление множества Д, Е, Ж, З на два множества Д и Е, Ж, З. Символу Д присваивается «1», а множеству Е, Ж, З присваивается «0».

На пятом этапе производится деление множества Е, Ж, З на два множества Е и Ж, З. Символу Е присваивается «1», а множеству Ж, З присваивается «0».

На шестом этапе производится деление множества Ж, З на два множества Ж и З. Символу Ж присваивается «1», а символу З присваивается «0».

Легко проверить, что данный код оказывается префиксным и средняя длина кодовой комбинации 1,915, что менее чем на 7 % превышает энтропию данного источника, равную 1,7813. A избыточность кода составит

.

Отметим, что хотя, деление на части с "примерно равными вероятностями" не является однозначной процедурой, но при увеличении длин блоков m укрупнённого источника сообщений эти погрешности бу­дут сглаживаться, а средняя длина при­ближаться к предельному значению.