8.7.4. Основные характеристики систем с решающей обратной связью
При приеме кодовой комбинации возможны три случая: комбинация принята без ошибок (Пр) (правильный прием) с обнаруженными (ОО) и необнаруженными ошибками (НО). Очевидно, что
,
(8.82)
где
– вероятности
указанных случаев соответственно (рис.
8.43).
Вероятность
правильного приема можно определить
из выражения (8.37) при условии, что в блоке
не произойдет ни одной ошибки
,
тогда
.
Вероятность обнаружения ошибки определится выражением
,
где
- вероятность того, что в блоке произошла,
хотя бы одна ошибка
,
- коэффициент
обнаруживаемых ошибок
,
где
-число возможных
кодовых комбинаций,
- число запрещенных кодовых комбинаций
(
- количество символов в блоке,
- количество проверочных символов).
Тогда
Тогда вероятность обнаружения ошибки будет равна
.
Вероятность необнаружения ошибки определится из выражения
,
где
- коэффициент необнаруживаемых ошибок
,
- число
разрешенных кодовых комбинаций.
,
при
.
Тогда вероятность необнаружения ошибки будет равна
.
При обнаружении
ошибок в принятой комбинации по обратному
каналу передается сигнал переспроса,
искажение или ложное формирование
которого приводит к ошибкам типа вставок
и выпадений. При отсутствии искажений
в сигнале переспроса (вероятность
)
процесс повторяется (на рис. 8.43 показан
переход в вершину Н с вероятностью 1).
Таким образом,
принятая комбинация выдается потребителю
информации с ошибкой с вероятностью
в следующих случаях:
- ошибки в принятой
комбинации не обнаруживаются с
вероятностью
;
- ошибки в принятой
комбинации обнаруживаются, но искажается
сигнал переспроса. Вероятность этого
события в соответствии с вероятностным
графом равна
.
Тогда
.
Вероятность возникновения переспроса кодовой комбинации в соответствии с вероятностным графом равна
.
В соответствии с вероятностным графом вероятность ошибки в системе с РОС можно определить по формуле
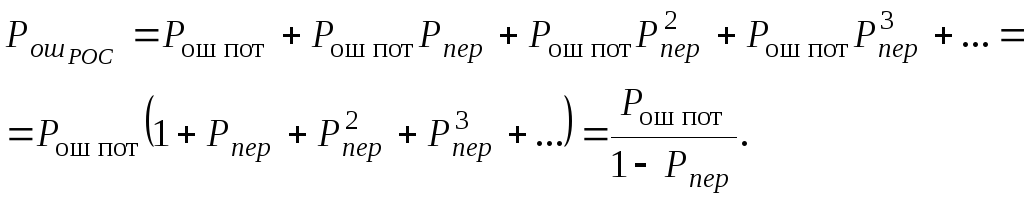
С учетом вероятности
того, что информация будет выдана
потребителю о ошибкой
и вероятности возникновения переспроса
вероятность ошибки в системе с РОС будет
равна
.
Как правило, в
системе приняты меры для ослабления
влияния искажений и ложного формирования
сигнала переспроса, следовательно,
вероятностью
можно пренебречь и соотношение принимает
вид
.
В полученном соотношении вероятность необнаружения ошибок зависит главным образом от свойств используемого метода обнаружения ошибок и от качества канала.
При обнаружении ошибки декодирующим устройством в системах с РОС производится переспрос группы кодовых комбинаций. Во время переспроса полезная информация не передается, поэтому скорость передачи информации уменьшается.
В этом случае
,
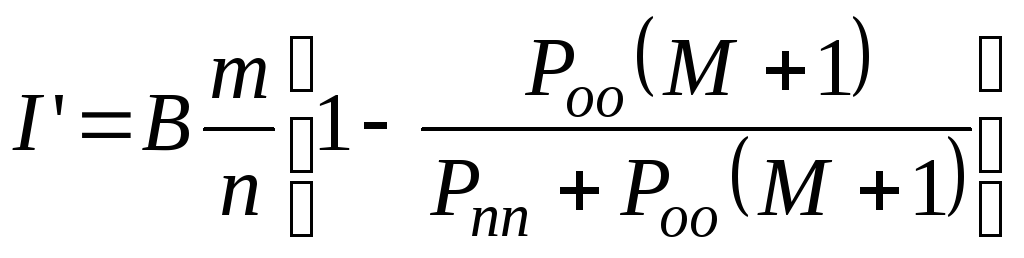где
- емкость накопителя,
- вероятность
обнаружения ошибки,
- вероятность
правильного приема,
В - скорость модуляции, Бод.
Емкость накопителя передатчика в числе кодовых комбинаций
,
где
- время распространения сигнала по
каналу,
- время передачи
кодовой комбинации,
- расстояние между
передатчиком и приемником,
- скорость
распространения сигнала по каналу связи
км/с (
),