1. Способы декодирования с обнаружением ошибок

Процедура декодирования циклического кода с обнаружением ошибок, по аналогии с процессом кодирования основана на использовании свойства делимости без остатка кодового многочлена Р(x) циклического (n,m)-кода на порождающий многочлен g(x). Поэтому алгоритм декодирования включает в себя деление принятого кодового слова, описываемого многочленом F(x) на g(x), вычисление и анализ остатка R(x). Если R(x)=0, то принятое кодовое слово считается неискаженным. Если R(x)0, то принятое кодовое слово стирается и формируется сигнал "ошибка".

2 Способы декодирования с исправлением ошибок

Декодирование заключается в определении номера искаженного разряда и его автоматического исправления. А также отделения информационных разрядов от контрольных.

Рассмотрим три методики декодирования

Определение искаженного разряда с помощью матрицы ошибок.

Матрица одиночных ошибок имеет вид

, где - единичная матрица;- прямоугольная проверочная матрица.

Строки матрицы определяются из выражений

- остаток от деления на образующий полином,

где - значениеi-той строки матрицы ;

i - номер строки матрицы .

Пример. Матрица для (7,4)-кода на основе порождающего многочленаимеет вид

.

Единичная матрица размерности 7х7

.

Рассчитаем проверочную матрицу .

При .

Определим остаток от деления на образующий полином.

.

При .

Определим остаток от деления на образующий полином.

.

При .

Определим остаток от деления на образующий полином.

111.

При .

101.

При .

100.

При .

010.

При .

001.

Тогда матрица ошибок

Для определения искаженного разряда необходимо определить остаток от деления принятой кодовой комбинации на порождающий многочлен.

Пример

Внесем искажения в четвертый разряд

Находим остаток

1 0 1 0 1 0 0
 1 1 0 1
1 1 1 1
 1 1 0 1
0 0 1 0 0 0
 1 1 0 1
1 0 1	- остаток

Находим строку в матрице ошибок с полученным остатком (синдромом) 1 0 1

Искаженный разряд – это разряд в данной строке, в которой стоит «1».

Искаженный разряд исправляем посредством сложения строки в матрице ошибок с полученной комбинацией

.

Сообщение исправлено.

Метод дополнительного деления первоначального остатка на образующий многочлен

Метод дополнительного деления основывается на предыдущем методе т.к. каждый такт дополнительного деления (приписывания нуля справа) соответствует переходу от данной строки матрицы ошибок (строка с первоначальным остатком) к строке следующей вверх матрицы.

Дополнительное деление продолжается до получения остатка с «1» в первом разряде и нулями в остальных разрядах, потому что этот остаток равен остатку последней строки матрицы ошибок. Отсчет искаженного разряда производится от старшего разряда сообщения, по количеству тактов дополнительного деления. Такой отсчет соответствует возвратному движению в матрице ошибок.

Пример.

Внесем искажения в четвертый разряд

Находим остаток

1 0 1 0 1 0 0
 1 1 0 1
1 1 1 1
 1 1 0 1
0 0 1 0 0 0
 1 1 0 1
1 0 1	- остаток

Д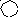ополниетльное деление

1 0 1 0	Дополнительное деление 1
 1 1 0 1
1 1 1 0	Дополнительное деление 2
 1 1 0 1
0 0 1 1 0 0	Дополнительное деление 3, 4
 1 1 0 1
0 0 1	- остаток

Понадобилось 4 такта дополнителоного деления. Тогда

.

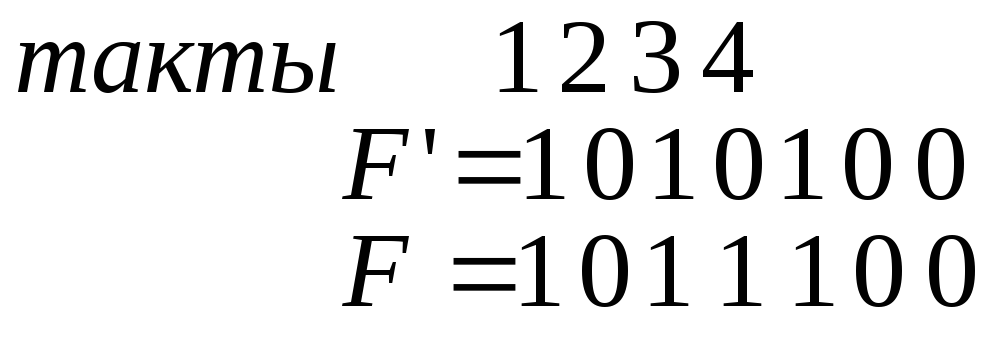Четвертый такт указывает номер искаженного разряда, который исправляем.

Метод циклических сдвигов

Метод циклических сдвигов заключается в следующем:

1. Находится остаток от деления на. Если остаток равен нулю, то ошибок нет.

2. Если остаток отличен от нуля, определяется вес остатка и выполнения условия, где- количество исправляемых ошибок.

Если условие выполняется, то производится суммирование по модулю 2 полученного остатка с комбинацией, из которой он получен. Затем производятся сдвиги вправо столько раз сколько было сделано сдвигов влево В результате получаем исправленной сообщение.

3. Если вес остатка больше кратности исправляемых разрядов, то производится сдвиг влево полученной комбинации, т.е. умножение кодовой комбинации на . И снова находится остаток от деления и переход к п.2.

Пример.

,

.

Внесем искажения в четвертый разряд

.

Находим остаток 1 0 1.

Вес остатка

.

1-й циклический сдвиг

Находим остаток

0 1 0 1 0 0 1
 1 1 0 1
0 1 1 1 0
 1 1 0 1
1 1 1	- остаток

Вес остатка .

2-й циклический сдвиг

Находим остаток

1 0 1 0 0 1 0
 1 1 0 1
1 1 1 0
 1 1 0 1
1 1 1 0
 1 1 0 1
0 0 1 1	- остаток

Вес остатка .

3-й циклический сдвиг

Находим остаток

0 1 0 0 1 0 1
 1 1 0 1
0 1 0 0 0
 1 1 0 1
0 1 0 1 1
 1 1 0 1
0 1 1 0	- остаток

Вес остатка .

4-й циклический сдвиг

Находим остаток

1 0 0 1 0 1 0
 1 1 0 1
0 1 0 0 0
 1 1 0 1
0 1 0 1 1
 1 1 0 1
0 1 1 0 0
 1 1 0 1
0 0 0 01	- остаток

Вес остатка .

Вес равен «1» поэтому циклические сдвиги закончились. Теперь необходимо остаток сложить с той комбинацией, с которой мы его получили

1 0 0 1 0 1 0

 0 0 0 1

1 0 0 1 0 1 1

Затем производятся сдвиги вправо столько раз, сколько было сделано сдвигов влево

1 0 0 1 0 1 1

1-й сдвиг

1 1 0 0 1 0 1

2-й сдвиг

1 1 1 0 0 1 0

3-й сдвиг

0 1 1 1 0 0 1

4-й сдвиг

1 0 1 1 1 0 0

Сообщение исправлено

.

Свойства циклических кодов по обнаружению ошибок

Свойства циклических кодов полностью определяются выбранным порождающим (образующим) многочленом .

I. Если порождающий многочлен содержит более одного члена, то циклический код обнаруживает все одиночные ошибки. При представлении циклического кода многочленами одиночная ошибка описывается одночленом, где- указывает номер искаженного разряда. Поскольку одночлен не делится на многочлен без остатка, то ошибка будет обнаружена.

2. Циклический код с порождающим многочленом обнаруживает все нечетные ошибки. Используя правила построения проверочной матрицы для, получим. При такой проверочной матрице остаток определяется суммой по модулю 2 всех элементов принятой кодовой комбинации (проверка на четность). Поэтому все искажения на нечетном количестве позиций будут обнаружены.

3. Циклический код обнаруживает все одиночные и двукратные ошибки, если разрядность кода не больше длины циклаиспользуемого порождающего многочлена, т.е.. Под длиной цикла многочлена понимают минимальный показатель степени двучлена, при котором этот двучлен делится без остатка на образующий многочлен.

4. Циклический код с многочленом степениобнаруживает все групповые ошибки длительностью вразрядов и менее. Любая групповая ошибка вразрядов описывается многочленом степени, т.е.. Многочлен же степенина многочлен степенине делится и, таким образом, ошибка обнаруживается.

5. Циклический код с порождающим многочленом степенине обнаруживаетчасть ошибок-й кратности.

6. Циклический код с порождающим многочленом степенине обнаруживаетчасть ошибок более-й кратности.

Анализируя перечисленные свойства циклического кода, можно увидеть, что способности кода по обнаружению и исправлению ошибок полностью определяются выбранным образующим многочленом .

При обнаружении ошибок стандартные многочлены имеют вид: ,при длине кодовой комбинации,

или ,при длине кодовой комбинации;

, при длине кодовой комбинации.

Разработан ряд методик по выбору порождающего многочлена . В литературе коды называют по фамилиям ученых, предложивших ту или иную методику. Так получили свое название коды Боуза-Чоудхури-Хоквингема (БЧХ), коды Рида-Соломона, коды Файра и др.

Укороченные циклические коды

Циклические коды предполагают равенство разрядности формируемой кодовой комбинации длине цикла порождающего многочлена, т.е. . Однако, это требование на практике трудно выполнимо, поскольку разрядность комбинаций, выдаваемых источником информации, зачастую отличается от целесообразной, в результате чего. В этих случаях циклический код преобразуют и используют так называемый укороченный циклический код, который получается из циклического путем исключения в нем определенного числа разрядов.

При этом число столбцов проверочной матрицы уменьшается на величину, равную числу исключаемых информационных разрядов, причем исключаются столбцы с наивысшими номерами. Свойства кода по обнаружению ошибок при этом не изменяются.

Принципы построения кодирующих и декодирующих устройств циклических кодов

Кодирующие и декодирующие устройства циклических кодов строятся на основе регистров с обратными связями. Такие регистры иногда называют многотактными линейными переключающими схемами. При кодировании и декодировании циклических кодов получаемый остаток содержит число разрядов, равное показателю степени порождающего многочлена . Поэтому регистр с обратными связями (ОС) должен содержатьячеек памяти. Как ранее указывалось, столбцы проверочной матрицыявляются остатками от деления одночленана. Разделить жепри помощи регистра с ОС это значит осуществить сдвиг записанной в этот регистр „1" натактов после ввода ее в первую ячейку. Таким образом, при каждом сдвиге записанной в регистр „1” должен получаться остаток, соответствующий делениюна. Следовательно, содержание регистра при каждом тактовом сдвиге должно соответствовать содержанию столбца проверочной матрицы.

В качестве примера на рис. 8.15 показаны схема регистра с ОС для порождающего многочлена и состояние ячеек этого регистра при сдвиге «1» записанных в первую ячейку (табл. 8.19). На конкретном примере покажем, что данный регистр производит операцию деления.

Пусть требуется закодировать кодовую комбинацию вида 1 1 0 1, многочлен которой имеет вид .

Разделим многочлен и отметим остатки, полученные перед каждым следующим тактом деления:

	х 6+ х 5+ х 3				х 3+ х+1
	х 6+ х 4+ х 3
		x5+ х 4
		x5+ х3+ х2
			x4 +х3+х2
			x4 +х2+ x
			х3+ x
			х 3+ х+1
			1				- остаток

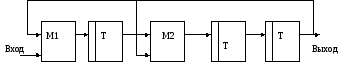
Рис. 8.15. Схема регистра с ОС для порождающего многочлена .

Табл. 8.19. К пояснению процесса кодирования

Деление сводится к последовательному сложению по модулю 2 делителя со старшими разрядами делимого или полученного остатка. Регистр с обратными связями производит аналогичные операции. Определим содержание регистра перед каждым тактом деления и сравним их с остатками, полученными путем обычного деяния.

Процесс деления в регистре производится только при поступлении "1" в цепь обратной связи. Поэтому содержание регистра, при котором "1" находится в последней ячейке, будет являться остатком перед следующим тактом деления. В табл. 8.19 показано содержание ячеек регистра по тактам. Сравнение остатков, полученных как при обычном делении, так и при делении с помощью регистра, показывает, что они полностью совпадают.

Регистры с обратными связями в соответствии с выбранным порождающим многочленом строятся по следующим правилам:

1. Число ячеек регистра выбирают равным степени порождающего многочлена .

2. Количество сумматоров по модулю 2 берется на единицу меньше числа ненулевых членов порождающего многочлена.

3. Входы всех ячеек регистра обозначают . Выход последней ячейки обозначается, а вход первой -.

Рис 8.16. Схема регистра с ОС для порождающего многочлена с обозначением.

4. Сумматоры по модулю 2 устанавливаются на входе тех ячеек, для которых в формуле порождающего многочлена имеет ненулевое значение. Например, для(рис. 8.16) сумматоры устанавливаются на входах ячеек 1 и 2 триггеров.

5. Выход последней ячейки соединяется со входами сумматоров.

6. Выходы предыдущих ячеек соединяются со входами последующих через сумматоры или без них, в зависимости от того, установлены они между ячейками или нет.

Рис.26.2 Кодирующее устройство

Структурная схема кодирующего устройства при порождающем многочлене показана на рис.8.17. В регистре с обратными связями передаваемая кодовая комбинация делится на исходный многочлен. При помощи линии задержки передаваемая комбинация смещается наразрядов (в данном случае=4), что равносильно умножению многочлена, отображающего передаваемую кодовую комбинацию, на.

Устройство функционирует следующим образом. Передаваемая кодовая комбинация последовательно подается на вход регистра и линии задержки. Ключ находится в положений «1» ключ- в положении «Включено» (рис.8.18).

После того как последний импульс с выхода линии задержки передан в линию связи, ключ . переключается в положение ,, 2"- в положение „Выключено" и содержимое регистра (остаток от деления) передается в линию связи (рис.8.19).

Приведенная схема кодирующего устройства обладает одним существенным недостатком. Кодированное сообщение задерживается на число тактов, равное числу ячеек регистра. Устранить такой недостаток можно при использовании кодирующего.устройства без линии задержки. В качестве примера на рис.8.20 изображена структурная схема такого устройства с .

Регистры с обратными связями для таких кодирующих устройств строятся по правилам, указанным ранее. Однако один из сумматоров устанавливается не на входе первой ячейки памяти, а на выходе последней ячейки.

Декодирующие устройства также строятся на основе использования регистров с обратными связями. На рис.8.21 приведена структурная схема декодирующего устройства, предназначенного для обнаружения ошибок. После приема кодовой комбинации в регистре с обратными связями образуется остаток . Если этот остаток равен 0, то сигнал запрета на выдачу принятой кодовой комбинации потребителю не выдается.

При использовании циклических кодов в качестве кодов с исправлением ошибок схема декодирующего устройства усложняется.

Кратко рассмотрим методику построения таких декодирующих устройств для наиболее простого метода исправления ошибок -последовательного.

Этот метод основан на следующем свойстве. Если возникшая в кодовой комбинации ошибка исправляема, то после введения принятой кодовой комбинации в регистр с ОС можно восстановить вектор ошибок. После поразрядного сложения этого вектора с вектором, отображающим принятую кодовую комбинацию, ошибка исправляется. Структурная схема такого декодирующего устройства приведена на рис.8.22.

Принятая кодовая комбинация поразрядно поступает в регистр со сдвигом и в регистр с ОС. Затем принятая комбинация последовательным кодом через сумматор по модулю 2 (М2) выдается потребителю. В то время, когда искаженный разряд будет на выходе регистра со сдвигом, при исправляемых кодом ошибках содержание регистра с ОС будет вполне определенным. Селектор выделяет эту известную кодовую комбинацию и выдает на сумматор по модулю 2 импульс для исправления искаженного разряда. Одновременно в регистр с ОС записывается кодовая комбинация, при помощи которой устраняется влияние исправленного разряда на содержание этого регистра.

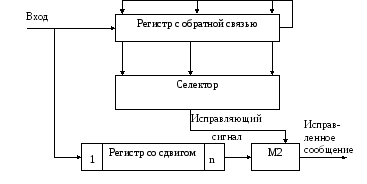
Рис 8.22. Декодирующее устройство с исправлением ошибок

Вероятности ошибочного декодирования циклических кодов

Вектором ошибки называется двоичная последовательность длины , в которой единицы стоят на позициях символов принятых с ошибкой. Отсюда вероятность не обнаружения ошибки заданным кодом равна вероятности появления в заданном дискретном канале векторов ошибок, совпадающих с кодовыми словами

Относительно просто эти вероятности могут быть рассчитаны для двоичного симметричного канала без памяти. В таком канале каждый двоичный символ с некоторой фиксированной вероятностью принимается правильно и с вероятностьюизменяется помехой на обратный. Передача/прием каждого символа полагается событием независимым (канал без памяти).

Если по такому каналу передается кодовое слово длины , то вероятность того, что не произойдет ни одной ошибки, равна.

Вероятность того, что будет одна ошибка в заданном символе, равна .

Вероятность того, что слово на выходе канала будет отличаться от передан­ного слова в заданных разрядах, т.е. вектор ошибок содержитединиц, равна

.

Вероятность того, что слово на выходе канала будет отличаться от передан­ного слова в любых разрядах, равна

,

где — число сочетаний из по .

Предположим, что некоторый линейный код (5,3) содержит одно нулевое слово (как всякий линейный код), два слова, вес которых равен 2, четыре слова — весом 3, одно слово — весом 4 (всего слов).

Вероятность необнаруживаемой этим кодом ошибки равна вероятности по­явления в ДСК векторов ошибок, совпадающих с кодовыми словами, т.е.:

В режиме исправления ошибок декодер вычисляет остаток от деления принятой последовательности на . Этот остаток называют синдромом. Принятый полином представляет собой сумму по модулю 2 переданного слова и вектора ошибок :

.

Тогда синдром , так как по определению циклического кода . Некоторому синдрому может быть поставлен в соот­ветствие определенный вектор ошибок . Тогда переданное слово находят, складывая.

Однако один и тот же синдром может соответствовать различным векто­рам ошибок. Предположим, синдром соответствует вектору ошибок. Но и все векторы ошибок, равные сумме, где- любое кодовое слово, будут давать тот же синдром. Поэтому, поставив в соответствие синдромувектор ошибок, мы будем осуществлять правильное декодирование в случае, когда действительно вектор ошибок равен , во всех остальныхслучаях декодирование будет ошибочным.

Для уменьшения вероятности ошибки декодирования из всех возможных векторов ошибок, дающих один и тот же синдром, следует выбирать в качестве исправляемого наиболее вероятный в заданном канале.

Например, для двоичного симметричного канала, в котором вероятность ошибочного приема двоичного символа существенно меньше вероятности правильного приема, вероятность появления векторов ошибок уменьшается с увеличением их веса . В этом случае следует исправлять в первую очередь вектор ошибок меньшего веса.

Если кодом могут быть исправлены только все векторы ошибок веса и меньше, то любой вектор ошибки веса отдоп будет приводить к ошибоч­ному декодированию.

Вероятность ошибочного декодирования будет равна вероятности появления векторов ошибок веса и больше в заданном канале. Для ДСК эта вероятность будет равна

Общее число различных векторов ошибок, которые может исправлять цик­лический код, равно числу ненулевых синдромов .