Глава 6. Оптимальные правила приема дискретных сообщений

6.1. Алгоритмы оптимального приема

З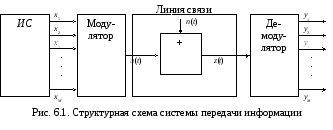адача помехоустойчивого оптимального приема дискретных сообщений является одной из важнейших задач теории электрической связи. При передаче сигналов по каналу с помехами полностью безошибочное восстановление переданного символа, невозможно, так как в силу случайной природы помех соответствие между переданным сигналом и принятым не однозначно.

На выходе модулятора в системах передачи происходит преобразование символа , в последователь­ность элементарных сигналов (рис.6.1). На вход демодулятора при передаче сигнала поступает колебание (сигнал + шум)

,

где - ад­дитивный шум в канале.

Если бы кодовые символы всегда совпадали с передаваемыми символами, то связь была бы безошибочной. Но, как известно, помехи приводят к невозможности с абсолютной достоверностью восстановить по принятому сигналу переданный кодовый символ.

Возникает вопрос: как принять решение о том, что в данный момент времени передано именно это сообщение?

Каждый демодулятор описывается законом, по которому поступивший на его вход непрерывный сигнал превращается в кодовый символ. Этот закон на­зывается правилом решения, а реализующая его схема — решающей. Демодулято­ры с различными правилами решения будут выдавать, вообще говоря, различ­ные решения, из которых одни верные, а другие — ошибочные.

В любом демодуляторе дискретных сообщений перед непосредственным принятием ре­шения приходящий сигнал подвергается той или иной обработке, целью которой является наилучшее использование различия между реализациями сигналов, соответствующих разным символам, а также отличия сигналов от помех.

Современная статистическая теория связи позволяет отыскать наилучшую операцию обработки входного сигнала z(t), обеспечивающую максимальное ка­чество оценки . При решении данной задачи полагают, что свойства источника сообщения и кодера известны. Кроме того, известен модулятор, т.е. задано, какая реализация эле­мента сигнала соответствует тому или иному кодовому символу, а также задана математическая модель непрерывного канала. Требуется определить, каков должен быть оптимальный демодулятор (правило решения), чтобы обеспечить наилучшее качество приёма.

Такая задача была впервые поставлена и решена (для гауссовского неискажающего канала с БГШ) В.А. Котельниковым. В этой постановке качество оценивалось вероятностью правильного приёма символа. Максимум этой веро­ятности при заданном виде модуляции В.А. Котельников назвал потенциаль­ной помехоустойчивостью, а демодулятор, обеспечивающий этот максимум, - идеальным приемником. Из этого определения следует, что ни в одном реаль­ном демодуляторе средняя вероятность правильного приёма символа не может быть больше, чем в идеальном приёмнике.

Изучим статистический подход к задаче приёма дис­кретных сообщений на фоне шумов. Пусть при передаче дискретных сообще­ний в месте приёма ожидаются сигна­лы , соответствующие кодовым символам . В течение отрезка времени [0, Т_с]¹⁾ на вход приёмного устройства по­ступает колебание z(t), которое вследствие искажений и помех в канале не сов­падает в точности ни с одним из элементов сигнала на передаче . Следова­тельно, в этом случае приёмное устройство должно выбрать одну из возмож­ных взаимоисключающих (альтернативных) гипотез: передавался кодовый сим­вол , т.е. ожидается сигнал ; передавался кодовый символ , т.е. ожида­ется сигнал ; передавался кодовый символ , т.е. ожидается сигнал . Для двоичной системы приёмное устройство выбирает одну из двух альтернативных гипотез о передаче символа 1 или 0.

Совокупность всех возможных реализаций z(t) можно интерпретировать точками в пространстве Z принимаемых сигналов. Графически изобразим реализации принимаемых сигналов и помех n(t) точками на плоскости (рис. 6.2) или соответствующими векторами на плоскости, откладываемыми от начала координат 0.

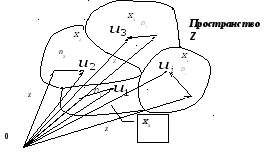
Рис.6.2. Разбиения пространства принимаемых колебаний

на непересекающиеся области

Если правило решения выбрано, то это означает, что каждой точ­ке пространства принимаемых колебаний (концу вектора ) приписывается одна из гипотез, т.е. определенный переда­ваемый кодовый символ . Пространство прини­маемых сигналов окажется при этом разбитым на непересекающихся областей пространства , каждая из которых соответствует принятию определённой гипотезы. В такой трактовке различные приёмные устройства отличаются друг от друга способом разбиения про­странства сигналов на области , т.е. правилом принятия решения²⁾. Возможное разбиение схема­тически показано на рис. 6.2. В двоичной системе пространство Z разбивают на две непересекающиеся области Х₀ и Х₁.

Если помехи отсутствуют, возможные значения z(t) изображаются точками . При наличии помехи и передаче сигнала с номером точка принимаемого колебания z отклоняется от точки . На рис. 6.2 это по­казано для сигналов , , и . Область содержит точку . В тех случаях, когда помеха не выводит точку за пределы области , решение оказывается верным при сигнале . В противном случае возникает ошибка. Из­меняя границы между областями, можно влиять на вероятность ошибочного приёма отдельных передаваемых символов.

Очевидно, всегда существует такое расположение областей, кото­рое в определённом смысле лучше всякого другого. Здесь, в зависимости от выполняемой задачи выбирается критерий определения границ областей пространства .

Статистические критерии оптимального приема дискретных сообщений

В теории электрической связи применяются следующие критерии оптимального приема дискретных сообщений:

1. критерий идеального наблюдателя (критерий Котельникова);

2. критерий минимального среднего риска (байесовский критерий);

3. критерий Неймана-Пирсона;

4. критерий Вальда.

Рассмотрим более подробно критерий идеального наблюдателя, который наиболее часто используется в связи.

Согласно критерию Котельникова качество демодуля­тора оценивают безусловной (средней) вероятностью правильного приема сим­вола.

Критерий идеального наблюдателя обеспечивается ре­шающей схемой, построенной по правилу максимума апостериорной вероятно­сти — решение , принимается в том случае, если выполняется система из неравенств:

(6.1)

Для двоичной системы сигналов это правило сводится к проверке не­равенства

. (6.2)

При выполнении неравенства (6.2) регистрируется символ 1, в противном случае - 0.

Апостериорная вероятность символа определяется согласно формуле Байеса

(6.3)

где априорная условная n-мерная плотность вероятности — функция правдоподобия i-й гипотезы (i=0…М-l) (определяется каналом связи),

— априорная вероятность передачи символа (т.е. та вероятность, которая имеет место до наблюдения и анализа, и определяемая статистикой ис­точника сообщения и правилом кодирования).

Подставив (6.3) в (6.1) и учитывая, что p(z) — безусловная плотность веро­ятности, не являющаяся функцией i, можно записать правило решения по кри­терию идеального наблюдателя в следующей форме:

или сокращённо:

. (6.4)

Приёмник, реализующий алгоритм (6.4), называется приёмником Котельникова. Для двоичной системы правило (6.4) сводится к проверке неравенства

, (6.5)

при выполнении которого регистрируется символ 1, а при невыполнении — 0.

Для построения решающей схемы по правилу (6.4) необходимо знать ап­риорные вероятности символов , а также свойства модулятора и канала, определяющие условные плотности — функции правдоподобия.

Рассмотрим пример для двоичной системы (рис.6.3), где графически представлены плотности вероятности на пространстве наблюдений.

Пример.

В системе связи передается двоичный сигнал: 1 или 0 с вероятностями , . В канале связи действует белый гауссовский шум с дисперсией . Шум имеет среднее значение равное 0 В при передаче 0 и среднее значение равное 1 В при передаче 1.

Какое решение примет приемник, если в момент принятия решения В (рис.6.3)?

Решение.

В соответствии с выражением (рис.6.3) определяются условные априорные вероятности «1» и «0».

,

.

Согласно (6.5)

,

.

Так как следовательно принимается решение, что передавалась «1».

Правило (6.4) можно записать иначе. Решение о том, что передавался символ должно приниматься, если для всех j i выполняются нера­венств

. (6.6)

Отношение в левой части этого неравенства называется отношением прав­доподобия двух гипотез: о том, что передавался символ , и о том, что переда­вался символ . Его обозначают _ij

. (6.7)

В случае, когда все символов передаются равновероятно, т.е.

(6.8)

правило (6.7) упрощается:

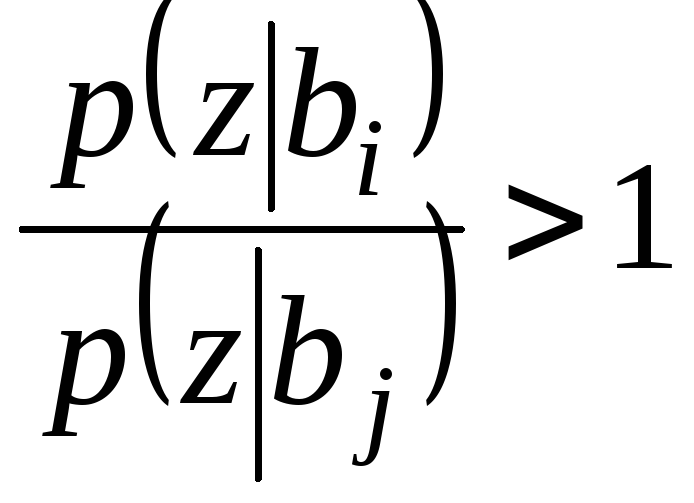, . (6.9)

Такое правило максимума правдоподобия реализу­ет критерий идеального наблюдателя при том условии, что все символы пере­даются равновероятно.

Выражение (6.9) является оптимальным правилом решения и называется правилом максимального правдоподобия, применяемое практически во всех системах связи, так как все кодовые символы в них передаются примерно с одинаковыми вероятностями.

Рассмотрим вывод формулы для построения оптимального приемника.

Напряжение на входе приемника

зависит только от аддитивной помехи. Помеха имеет случайный характер и подчиняется нормальному закону распределения:

,

а значит и напряжение на входе приемника, также будет подчиняться нормальному закону.

Рассмотрим двоичную систему. Условные плотности вероятности для и будут равны:

,

.

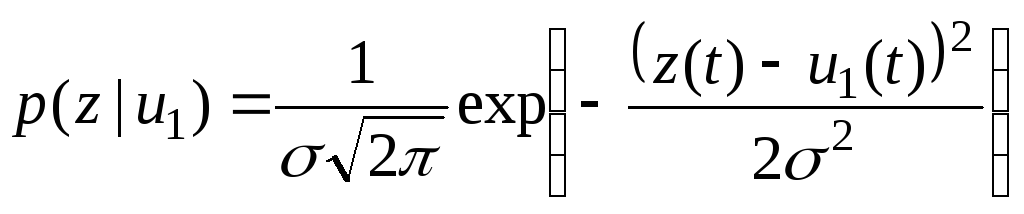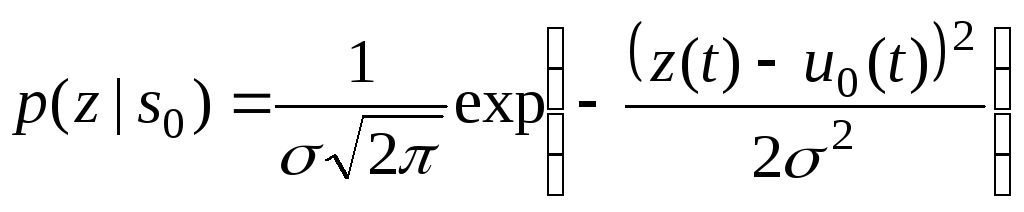Найдем отношение правдоподобия между реализациями:

,

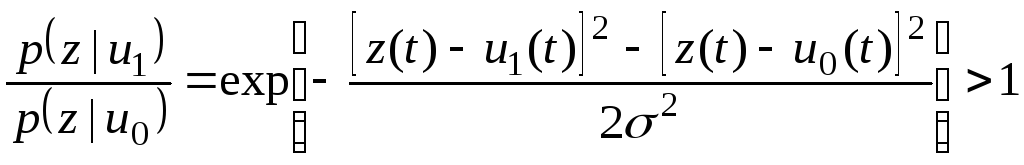где z(t) – напряжение на входе приемника; ² – средняя мощность шума.

.

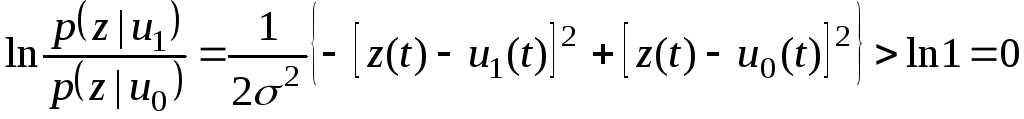Тогда можно записать

.

Или

.

Проинтегрировав и усреднив его за время действия одной реализации, равное периоду получим правило принятия решения в пользу реализации .

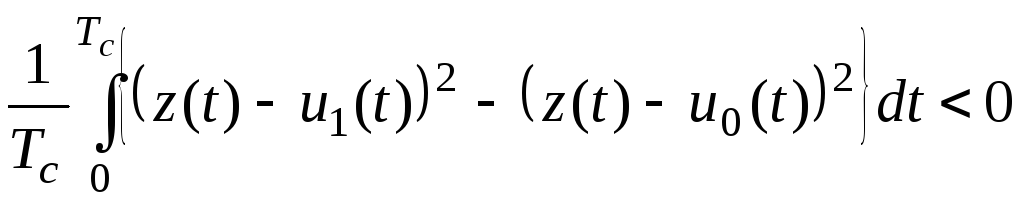
Полученное выражение преобразуем к виду:

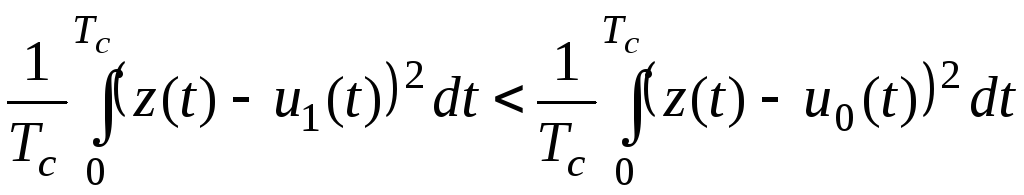. (6.10)

В формуле (6.10) реализуется признак минимального среднеквадратичного отклонения, то есть в сигнале распознается та реализация ( или ) относительно которой будет меньшим.

Указанное правило принятия решения можно записать следующим образом:

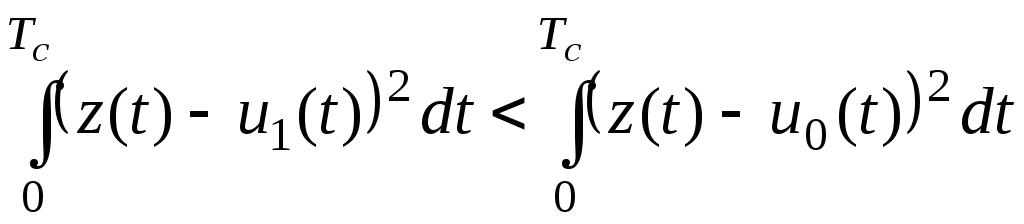. (6.11)

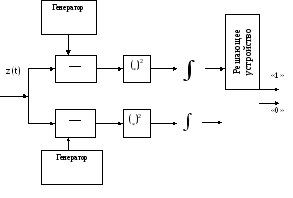
Рис. 6.4. Структурная схема оптимального приемника (6.11)

Отметим, что именно в таком виде впервые получил алгоритм оптимально­го приёма В.А. Котельников. Схема оптимального приемника представлена на рис. 6.4.

Преобразуем (6.10)

,

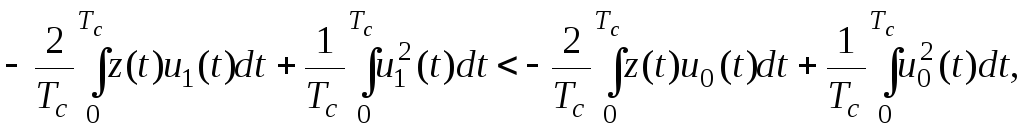
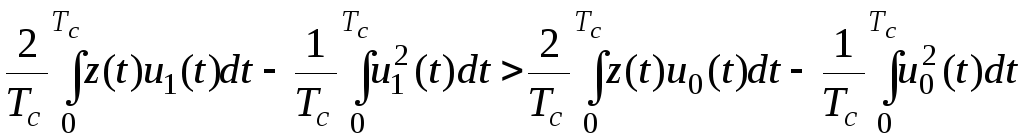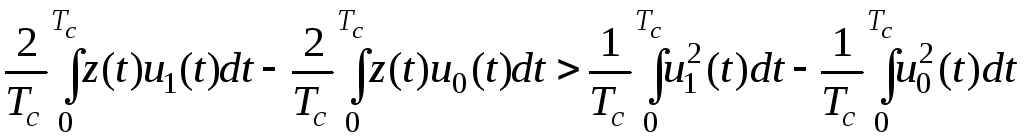. (6.12)

Зная, что: ; 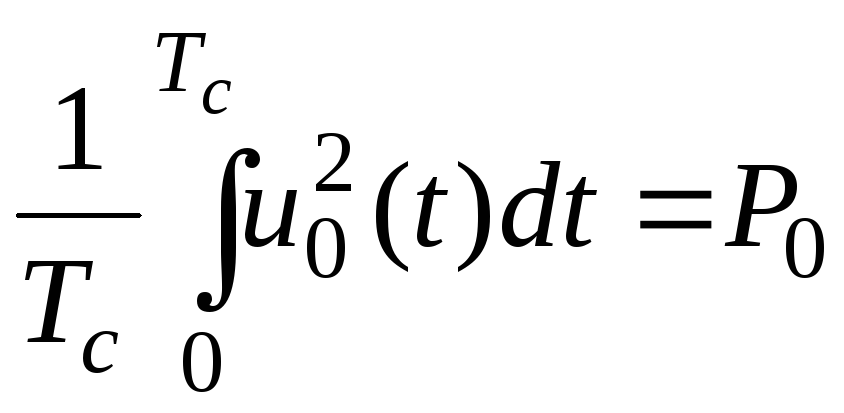, где P₁ и P₀ – средние мощности реализации сигнала на входе приемника получим:

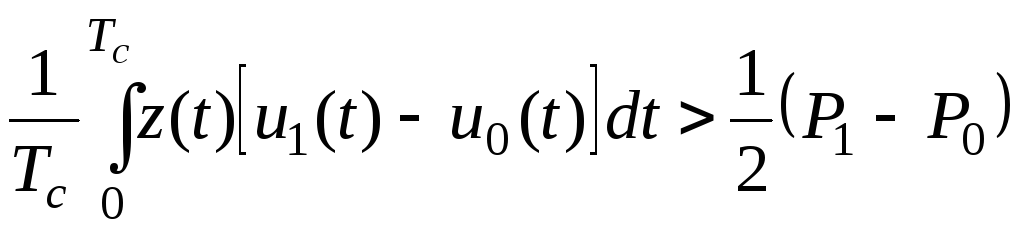. (6.13)

Полученный критерий позволяет синтезировать схему оптимального приемника (рис. 6.5).

Рис. 6.5. Структурная схема оптимального приемника (6.13)

Назначение элементов схемы и принцип работы схемы. Генераторы и вырабатывают соответствующие реализациям сигналы, которые поступают на вход вычитателя. Результирующий сигнал поступает на вход умножителя, на второй вход которого поступает входной сигнал z(t). Преобразованный сигнал интегрируется в интеграторе и поступает на вход схемы сравнения, на второй вход которого поступает сигнал .

• Если 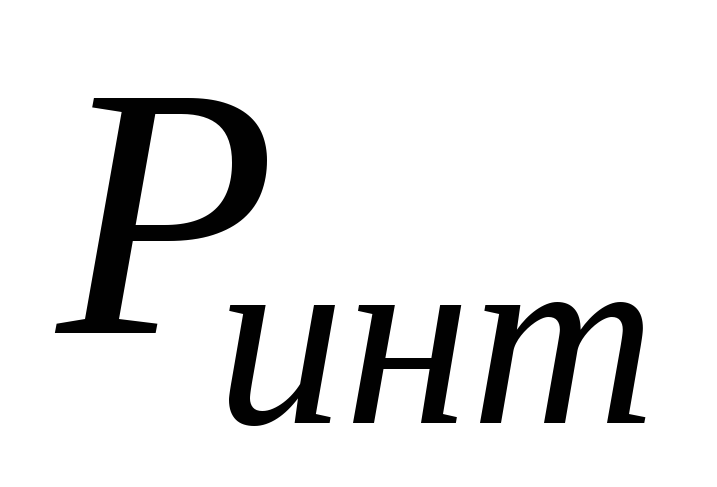> 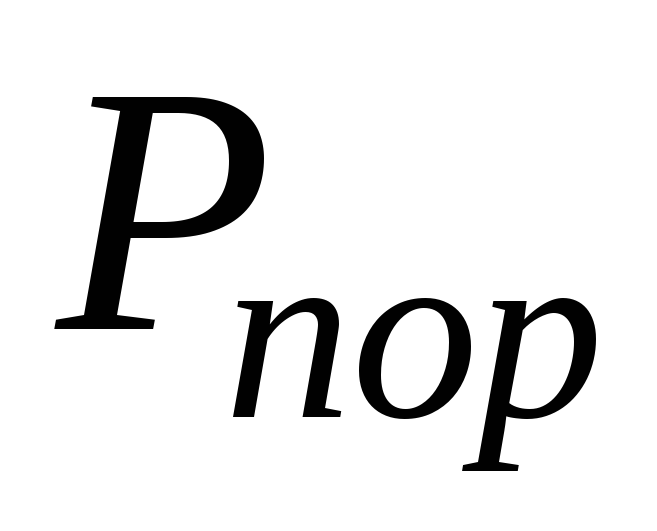то, схема принимает решение, что был передан сигнал 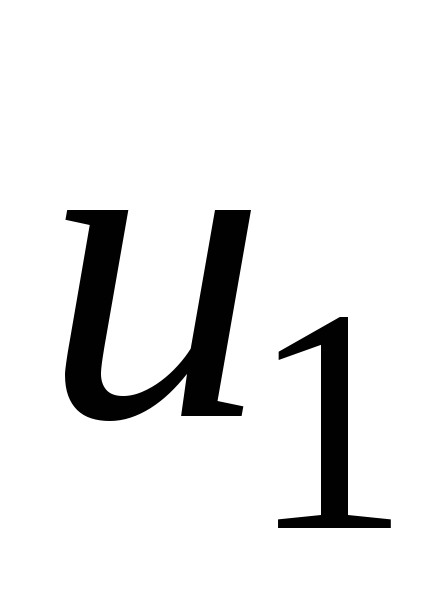("1");

• Если < то, схема принимает решение, что был передан сигнал 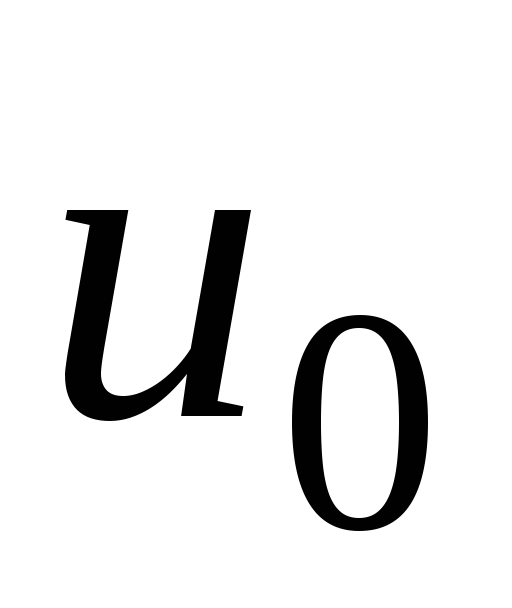("0").

Подбором достигается правильность принятия решения на определение соответствующей копии сигнала. может устанавливаться автоматически и зависеть только от входной мощности сигнала.