3 Функціональні відношення

3.1 Мета заняття

Ознайомлення на практичних прикладах з основними поняттями теорії функціональних відношень. Вивчення основних типів відображень (функцій). Вивчення інструментів наочного зображення функціональних відношень між множинами.

3.2 Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до практичного заняття необхідно повторити лекційний матеріал, розділи літератури [1-10] з таких питань: поняття функціонального відношення; способи задання функціональних відношень; поняття відображення (функції); область визначення та область значень функціональних відношень; основні типи відображень (функцій).

Підготовка і виконання практичного заняття проводиться за два етапи. Перший етап пов’язаний з вивченням на практичних прикладах таких основних понять і визначень функціональних відношень: функціональне відношення; функція; відображення; часткова функція; образ; прообраз; сюр’єктивна функція (сюр’єктивне відображення); ін’єктивна функція (ін’єктивне відображення); бієктивна функція (бієктивне відображення); взаємно однозначне відображення.

Під час виконання першого етапу студент повинен запропонувати і записати індивідуальний приклад для кожного з розглянутих вище понять і визначень.

Другий етап виконання практичного заняття пов’язаний з розв’язанням практичних завдань, які представлені у підрозділі 3.3, на основі запропонованих типових прикладів (див. підрозділ 3.4).

3.3 Контрольні запитання і завдання

3.3.1 Контрольні запитання

1. Яке відношення називається функціональним?

2. Яке функціональне відношення називається всюди визначеним?

3. Як виглядає матриця функціонального відношення?

4. Яке функціональне відношення називають відображенням множини 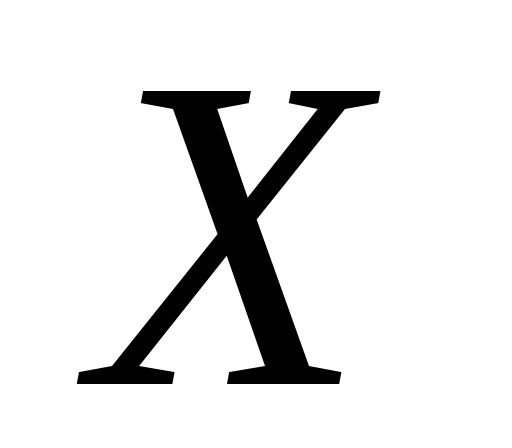в?

5. Що таке сюр’єкція?

6. Яке відображення називається ін’єктивним?

7. Що таке бієкція?

8. Яке відображення називається взаємно однозначним?

9. Що називається образом елемента?

10. Що таке прообраз елемента?

11. Чим характеризується граф і матриця сюр’єктивного, ін’єктивного, бієктивного відображення?

12. Перелічить основні властивості відображень.

3.3.2 Контрольні завдання

Завдання 1.

Нехай задані відношення: а) ; б); в); г). Які з наведених вище відношень є функціями, якщоі дійсні числа, належить області визначення, а області значень?

Завдання 2.

Нехай  множина мешканців України. Указати, які з можна вважати функціями, якщо вони означають: а); б); в); г).

Завдання 3. Нехай , де множина дійсних чисел. Знайти область визначення та область значень функцій:

а) ; б); в); г); д).

Завдання 4. Нехай  множина неупорядкованих трійок натуральних чисел. Відображенняставить у відповідність кожній трійцісуму.

Записати прообраз для кожного з перших шести натуральних чисел.

Завдання 5. Знайти обернену функцію для кожної з наступних функцій:

а) ; б); в).

Завдання 6. З’ясувати, які з наведених нижче функцій, у яких область визначення та область значень збігаються з дійсною числовою віссю, є ін’єк тивними, сюр’єктивними, мають обернену функцію?

а) ; б); в); г); д).

3.4 Приклади аудиторних і домашніх завдань

Завдання 1. Нехай , а. Відношеннязадане як. Чи є таке відношення функцією?

Розв’язок.

Відношення є функцією зв, тому що, і кожний з елементівприсутній як перший компонент упорядкованої пари зрівно один раз.

Завдання 2. Нехай , множина дійсних чисел. Знайти область визначення та область значень функції .

Розв’язок.

Область визначення функції (множина дійсних чисел), область значень функції.

Завдання 3. Знайти обернену функцію для .

Розв’язок.

Обертаючи функцію, одержуємо . Це те ж саме, що. Вирішуючи рівняння відносно, одержуємо.

Завдання 4. Нехай в множина дійсних чисел, і функція визначена як. Чи є функція сюр’єкцією, ін’єкцією й бієкцією?

Розв’язок.

Функція не є сюр’єктивною, оскільки не існує такого дійсного числа , для якого. Функція не є ін’єктивною, тому що, але. Помітимо, якщоі множина додатних дійсних чисел, тоді функція є ін’єктивною і сюр’єктивною.