
ман для 1ПМ-11 / 2 курс 2011 / практика / Границя послідовності / практика № 2
.docМіністерство освіти і науки, молоді та спорту України
Горлівський технікум Донецького національного університету
ПРАКТИЧНЕ ЗАНЯТТЯ № 2
з теми: «Обчислення границь числових послідовностей.»
Модуль КЗН-02. ПР.О.03.02 Границя послідовності
Дисципліна: «Математичний аналіз»
Розглянуто та схвалено Розробив викладач
на засіданні циклової Велікодна О. В.
комісії інформаційних технологій
та прикладної математики.
протокол № 1 від 30.08.2011 р.
Голова циклової
комісії ІТ та ПМ І. П. Сошина
ПЛАН ЗАНЯТТЯ
Дата: курс: ІІ
Викладач: Велікодна Ольга Володимирівна.
Тема: Обчислення границь числових послідовностей.
Мета:
-
Дидактична: поглибити поняття границі числової послідовності, систематизувати знання про основні властивості границі числової послідовності, оволодіти вмінням знаходити границю числової послідовності.
-
Виховна: підвищити рівень засвоєння навчального матеріалу, розвивати наукове мислення, усне мовлення студентів.
-
Методична: вдосконалювати методику проведення практичних занять з використанням технології проблемного та проектного навчання.
Вид: практичне заняття № 2
Тип: практичне заняття – дослідження.
Методи та форми проведення заняття: практичні, дедуктивні, проблемно – пошукові, фронтальна, групова робота.
Наочні посібники: -
Роздавальний матеріал: тестові завдання до актуалізації знань, картки - завдання до самостійного виконання студентами.
Обчислювальні засоби: -
Література:
-
Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.
-
Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.
-
Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.
-
Марон А. И. Дифференциальное и интегральное исчисление в примерах и задачах. – М.: Наука, 1973.
ХІД ЗАНЯТТЯ.
-
Організаційна частина:
-
відсутні;
-
підготовка до заняття;
-
перевірка д/з.
-
Мотивація навчальної діяльності студентів:
-
Актуалізація опорних знань:
-
Контроль за підготовкою студентів до практичного заняття:
-
Інструктаж щодо виконання практичної роботи.
-
Видача завдань для виконання роботи.
-
Виконання студентами практичної роботи.
-
Оформлення індивідуальних звітів виконаної роботи, захист практичної роботи.
-
Підведення підсумків. Оцінювання.
-
Домашнє завдання:
Конспект практичного заняття № 2.
Тема: «Обчислення границь числових послідовностей.»
-
Виконати тестове завдання.
-
Дослідити на збіжність за допомогою критерію Коші можна:
а) довільну збіжну послідовність;
б) довільну послідовність;
в) тільки розбіжну послідовність;
г) тільки послідовність, що збігається до нуля;
-
Дві послідовності збігаються. Тоді їх різниця є послідовність, яка
а) не обмежена зверху;
б) збігається;
в) розбігається;
г) може як збігатись, так і розбігатись;
-
Яка послідовність має три часткових границі?
а)
![]() ;
;
б) не має жодна;
в) (-1)ⁿ;
г)
![]() ;
;
-
Нехай послідовність {Xn} необмежена. Яке твердження вірне?
а) послідовність {Xn} є нескінченно великою;
б) послідовність {Xn} розбіжна;
в) послідовність {Xn} є обмеженою знизу;
г) послідовність {Xn} монотонно зростає;
-
Довільна обмежена послідовність
а) має часткову границю;
б) має скінчену границю;
в) має нескінченну часткову границю;
г) має нескінченну границю;
-
Довільна монотонна послідовність
а) має скінчену або нескінчену границю;
б) зростає;
в) збігається;
г) обмежена;
-
Чому дорівнює
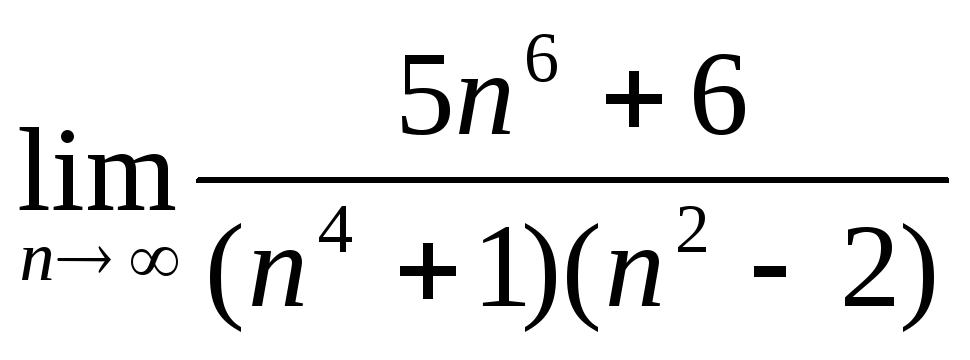 ?
?
а) ∞;
б) 1;
в) 5;
г) 6;
-
Яка послідовність не є нескінченно великою?
а) lg(ln n);
б) (-1)ⁿn;
в)
![]() ;
;
г)
![]() ;
;
-
Якщо послідовність збігається, то
а) будь – яка її підпослідовність збігається;
б) будь – яка її підпослідовність монотонна;
в) вона необмежена;
г) вона має необмежену підпослідовність;
-
Нехай а>0. Тоді
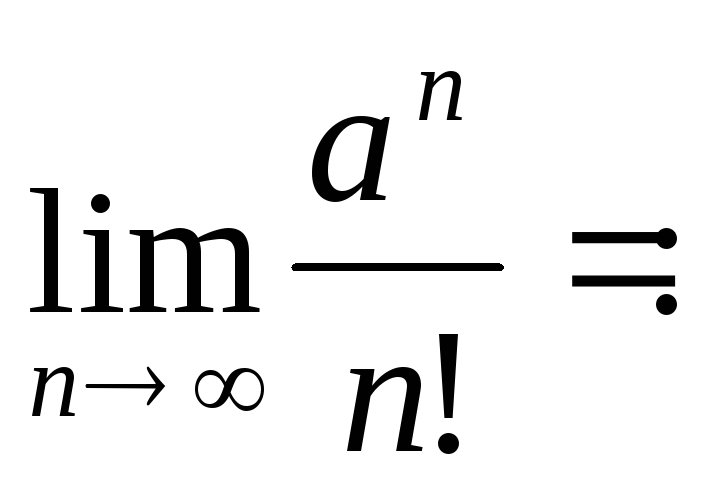
а) π;
б) +∞;
в) е;
г) 0;
-
Якщо послідовність
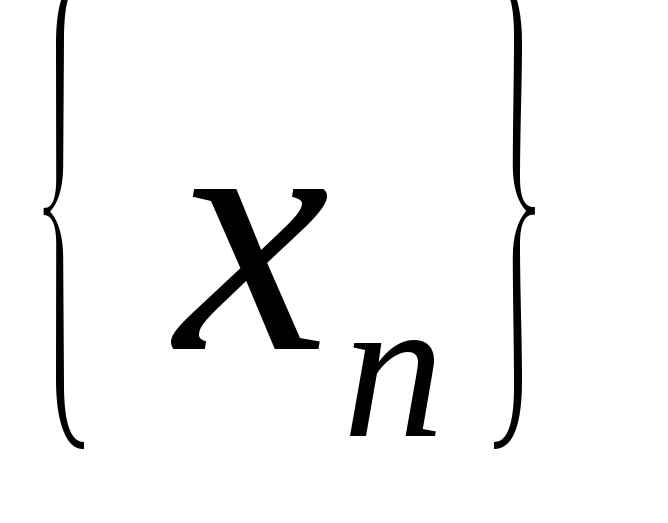 є нескінченно великою, то вона:
є нескінченно великою, то вона:
а)
![]() ;
;
б) необмежена;
в)
![]() ;
;
г) зростає;
-
Послідовність
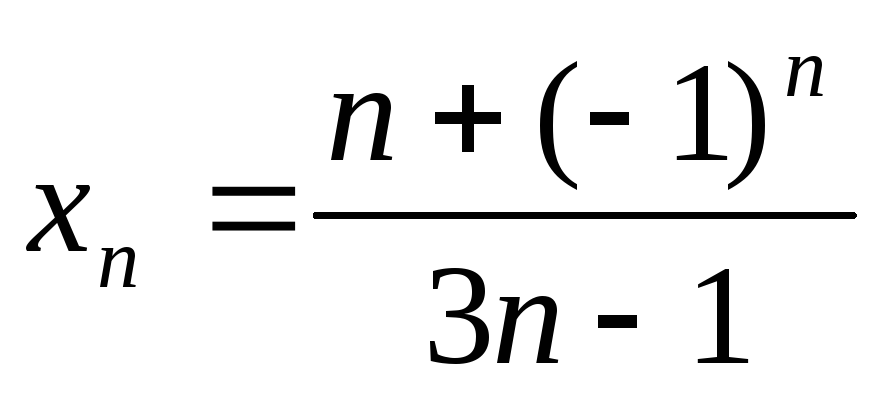 є
є
а) обмеженою;
б) необмеженою;
в) нескінченно великою;
г) нескінченно малою;
-
Нехай {αn} та {βn} нескінченно малі послідовності, αn ≠ 0. Яке твердження вірне?
а)
послідовність
![]() є нескінченно великою;
є нескінченно великою;
б)
послідовність
![]() є нескінченно малою;
є нескінченно малою;
в)
послідовність
![]() є нескінченно малою;
є нескінченно малою;
г)
послідовність
![]() ,
де с =const ≠0 є нескінченно великою;
,
де с =const ≠0 є нескінченно великою;
-
Нехай Y – множина значень послідовності. Тоді
а) Y може складатись з одного елемента;
б) Y має хоча б одну точку границі;
в) Y може складатись з довільного раціонального числа елементів;
г) Y – обмежена;
-
Яке твердження є вірним?
а) якщо послідовність не має границі, то вона не є обмеженою;
б) якщо послідовність обмежена, то вона має границю;
в) якщо додатна послідовність прямує до нуля, то вона монотонна;
г) якщо послідовність обмежена і монотонна, то вона має границю;
-
Нехай X – множина значень послідовності {xn}. Тоді
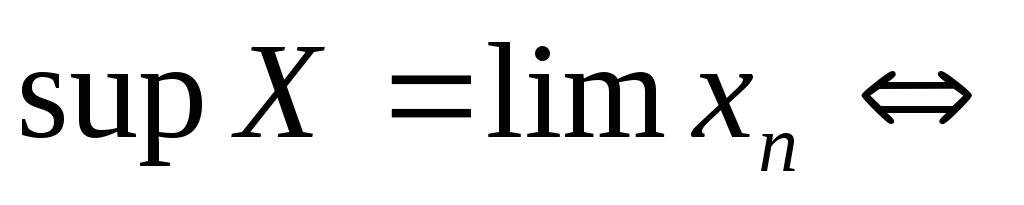
а) {xn} – монотонна;
б) {xn} – строго монотонно зростаюча;
в) завжди;
г) серед відповідей а) – в) вірної немає;
-
Чому дорівнює
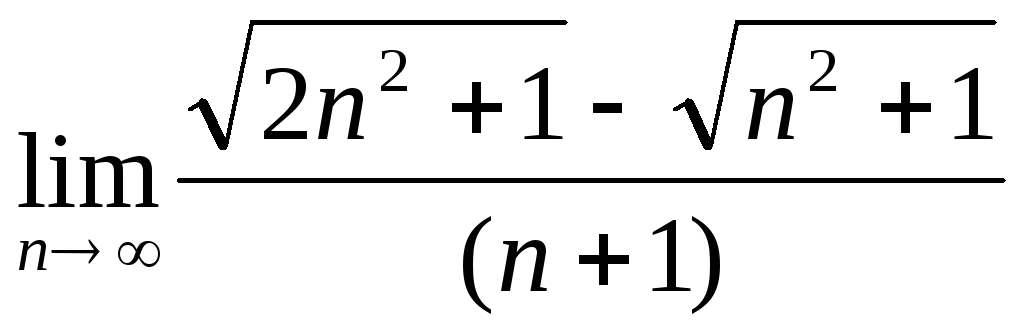 ?
?
а) інша відповідь;
б)
![]() ;
;
в) 2;
г)
![]() ;
;
-
Найбільша частинна границя послідовності є:
а) її границею;
б) числом, що обмежує її зверху;
в) її найбільшим елементом;
г) її верхньою границею;
-
Скільки граничних точок має послідовність
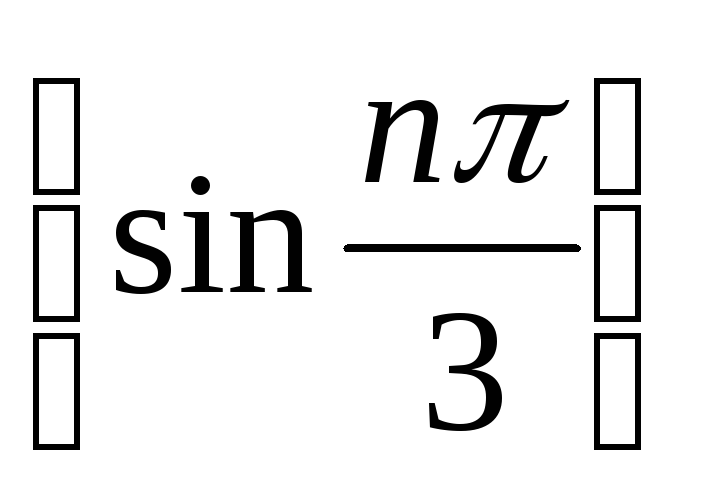 ?
?
а) 3;
б) 2;
в) 4;
г) 6;
-
Послідовність {xn} є фундаментальною. Чи обов'язково вона є
а) монотонно зростаючою;
б) обмеженою зверху;
в) монотонно спадною;
г) не монотонною;
-
Яка з послідовностей розбіжна?
а)
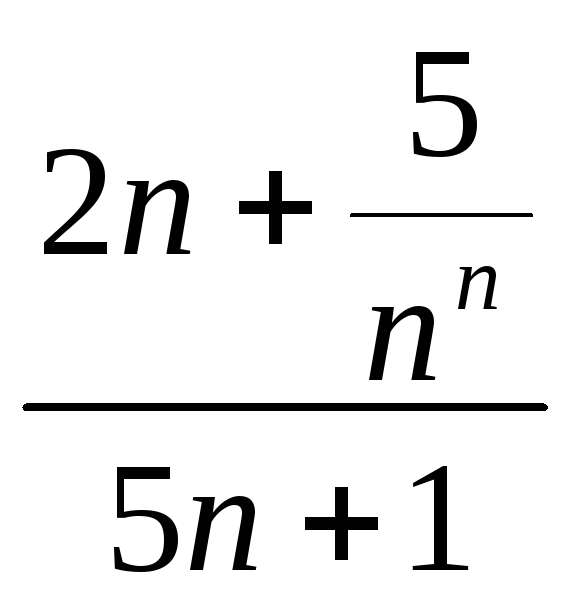 ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
-
Чому дорівнює
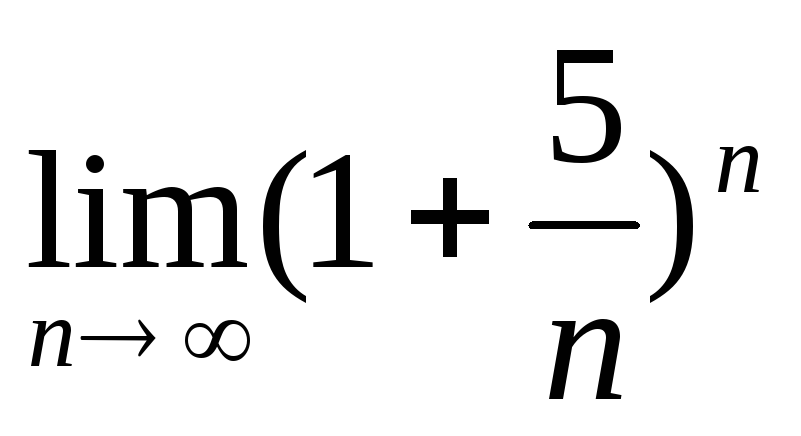 ?
?
а)
![]() ;
;
б) +∞;
в) 1;
г)
![]() ;
;
-
Нехай {Xn} – збіжна послідовність, {Yn} – розбіжна послідовність. Яке твердження правильне?
а) {Xn·Yn} – розбіжна;
б) {Xn·Yn} – збіжна;
в) {Xn ± Yn} – збіжна;
г) {Xn ± Yn} – розбіжна;
-
Дві послідовності збігаються. Тоді їх сума є послідовність, яка
а) може як збігатись, так і розбігатись;
б) збігається;
в) не обмежена зверху;
г) розбігається;
-
Послідовність {Xn} – строго монотонна, якщо
а) {Xn} – обмежена;
б) (Xn+1 - Хn)( Xn - Хn -1) > 0, n = 2, 3, 4,…;
в)
існує
![]() ;
;
г)
існує
![]() ;
;
-
Чи є послідовність{Xn},
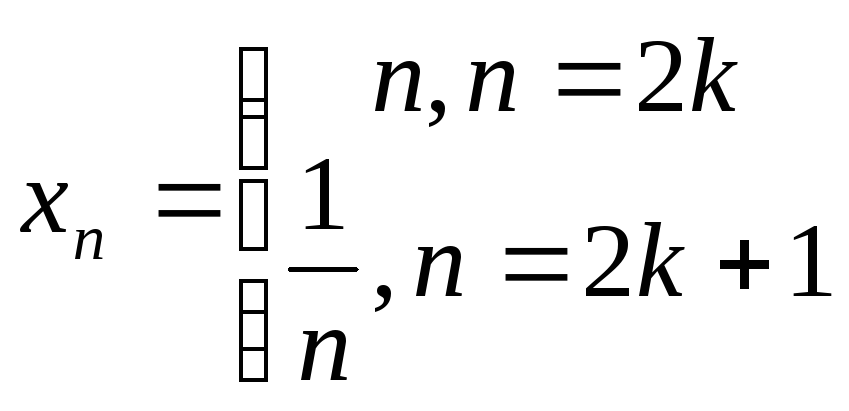
а) нескінченно великою;
б) обмеженою знизу;
в) нескінченно малою;
г) обмеженою зверху;
-
Послідовність {Xn} називається нескінченно малою, якщо
а) вона розбігається;
б) вона збігається;
в) її границя дорівнює певного знака нескінченності;
г)
![]() ;
;
-
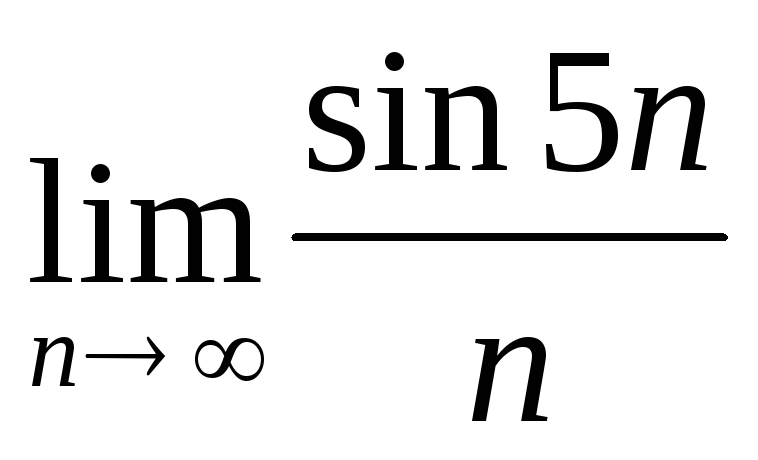 дорівнює
дорівнює
а) ∞;
б) не існує;
в) 1;
г) 0;
-
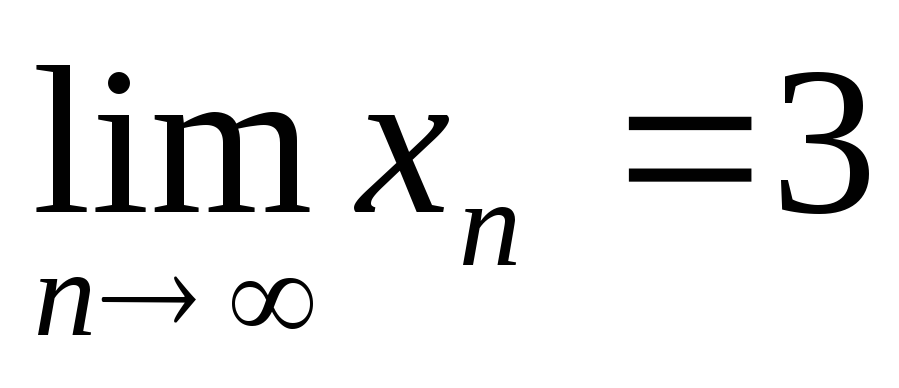 .
Яке твердження правильне?
.
Яке твердження правильне?
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
-
Нехай {Xn} – збіжна. Тоді {СXn} – збіжна:
а) тільки при С = 1;
б)тільки при С = 0;
в) для довільного С;
г) ніколи (таких С не існує);
-
Нехай
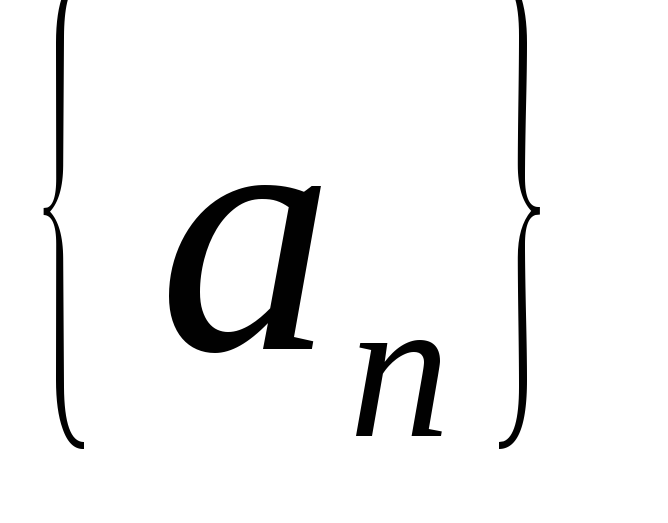 - нескінченно мала послідовність (
- нескінченно мала послідовність ( ),
),
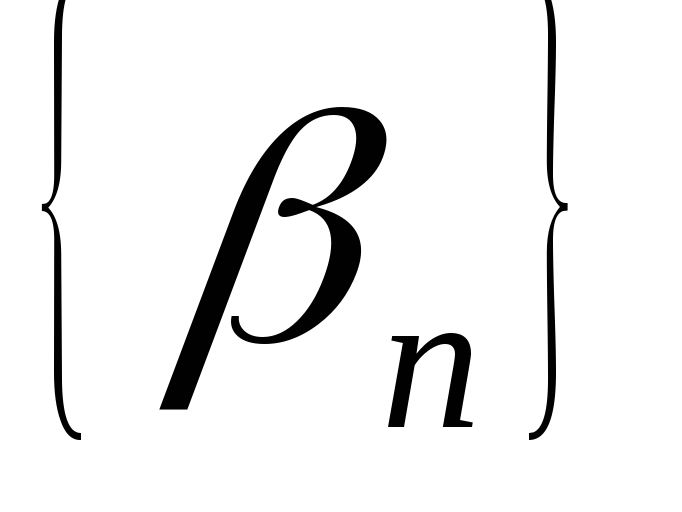 - збіжна послідовність. Яке твердження
правильне?
- збіжна послідовність. Яке твердження
правильне?
а)
![]() - розбігається;
- розбігається;
б)
![]() -
збігається;
-
збігається;
в)
![]() -
збігається;
-
збігається;
г)
![]() - збігається;
- збігається;
-
Якщо послідовність обмежена, то
а) вона монотонна;
б) будь – яка її підпослідовність збігається;
в) вона збігається;
г) вона має підпослідовність, яка збігається;
-
Нехай Xn – збігається, а послідовність Yn – розбігається. Тоді їх сума Xn + Yn є послідовність, яка:
а) фундаментальна;
б) розбігається;
в) може як збігатись, так і розбігатись;
г) збігається;
-
Якщо послідовність збігається, то
а) вона має необмежену підпослідовність;
б) вона має монотонну підпослідовність;
в) вона необмежена;
г) будь – яка її підпослідовність монотонна;
-
Нехай
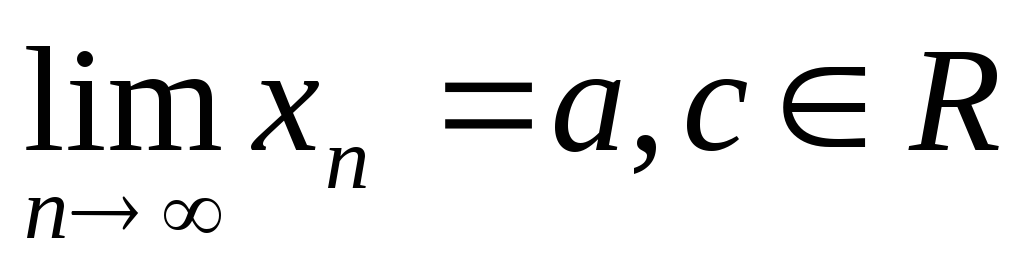 .
Тоді
.
Тоді
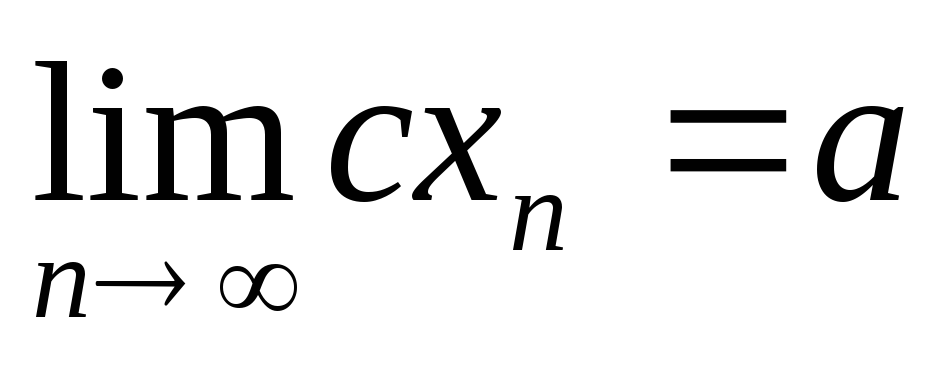 :
:
а) для довільного c;
б) ніколи ( таких с не існує);
в) якщо с = 0;
г) якщо с = 1;
-
Скільки граничних точок має послідовність {cos
 }
?
}
?
а) 3;
б) 8;
в) 5;
г) 2;
-
Послідовність {xn} називається фундаментальною, якщо
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
-
xn → a > 0 коли n → ∞. Яке з тверджень невірне?
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
-
Нехай
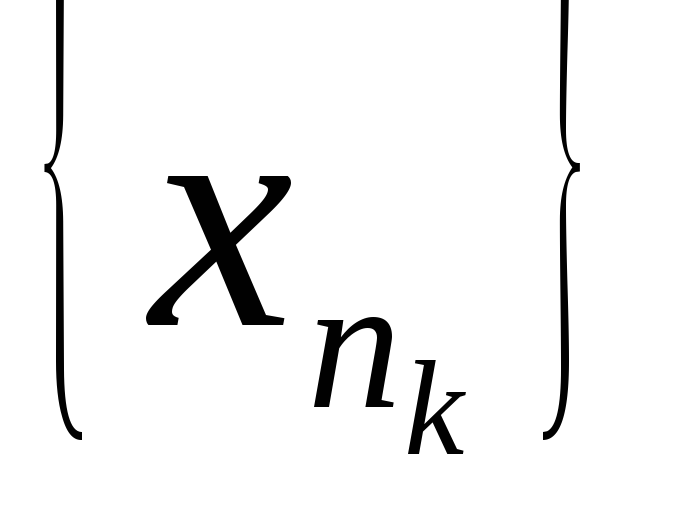 та
та
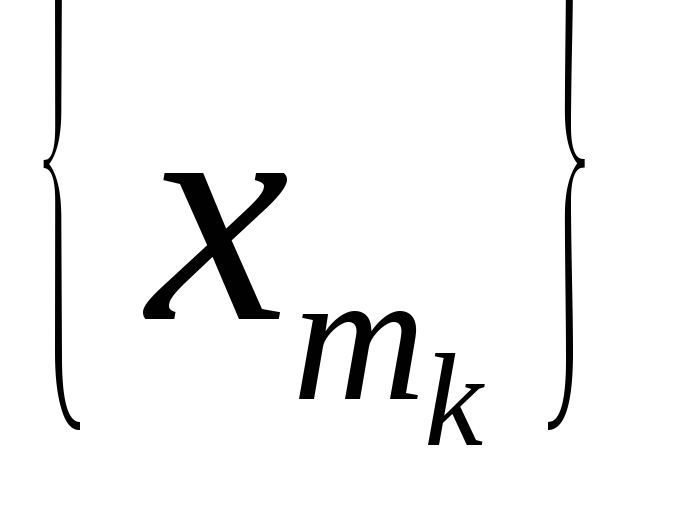 - дві підпослідовності послідовності
- дві підпослідовності послідовності
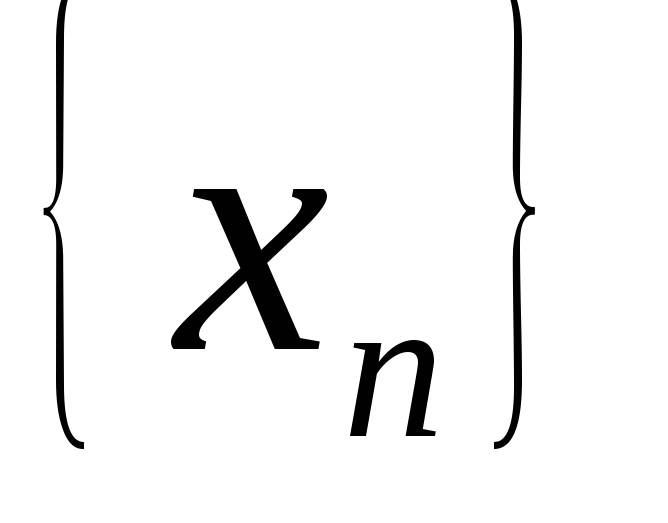 .
Яке твердження правильне?
.
Яке твердження правильне?
а) якщо
![]() ,
то
,
то
![]()
![]() і
і
![]()
![]() ;
;
б) якщо
![]()
![]() і
і
![]()
![]() ,
то
,
то
![]()
![]() ;
;
в) якщо
![]() розбігається, то
розбігається, то
![]() та
та
![]() - необмежені;
- необмежені;
г) якщо
![]() обмежена, то
обмежена, то
![]() збіжна;
збіжна;
-
Довільна фундаментальна послідовність
а) нескінченно велика;
б) нескінченно мала;
в) монотонна;
г) обмежена;
-
Яке твердження еквівалентно умові
 ?
?
а)
![]() ;
;
б)
![]() ;
;
в)
послідовність
![]() є нескінченно малою;
є нескінченно малою;
г)
![]() ;
;
-
Якщо послідовність
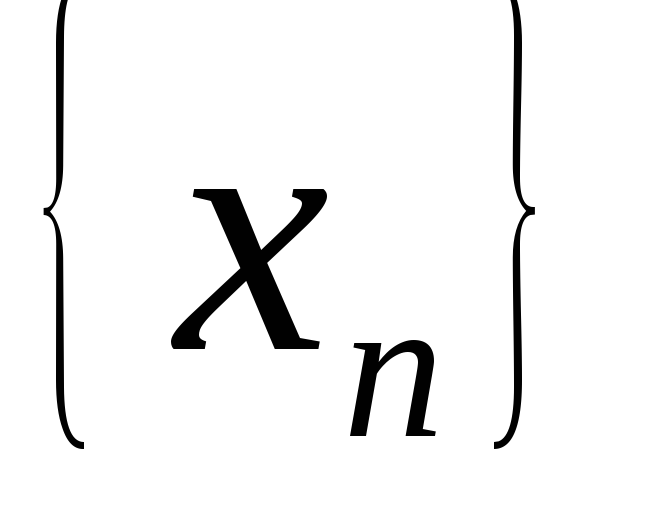 збігається, то вона:
збігається, то вона:
а) обмежена;
б) зростаюча;
в) нескінченно мала;
г) монотонна та обмежена;
-
Нехай
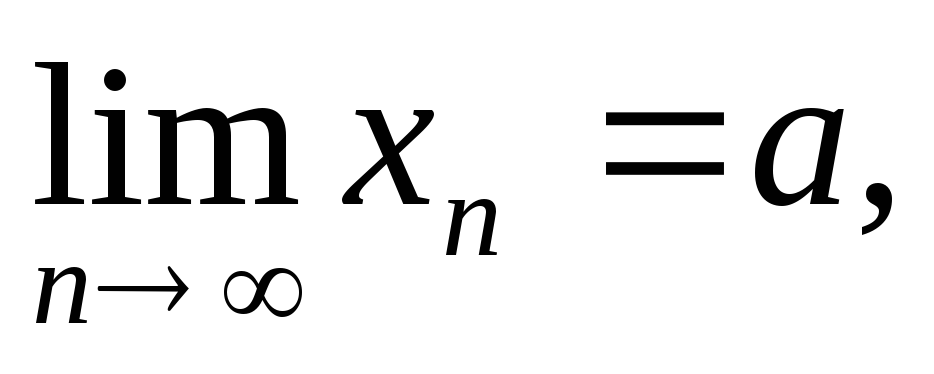
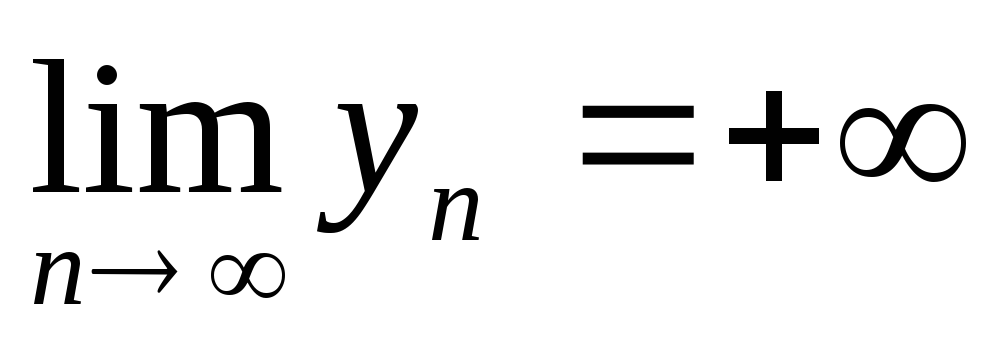 .
Тоді послідовність
.
Тоді послідовність
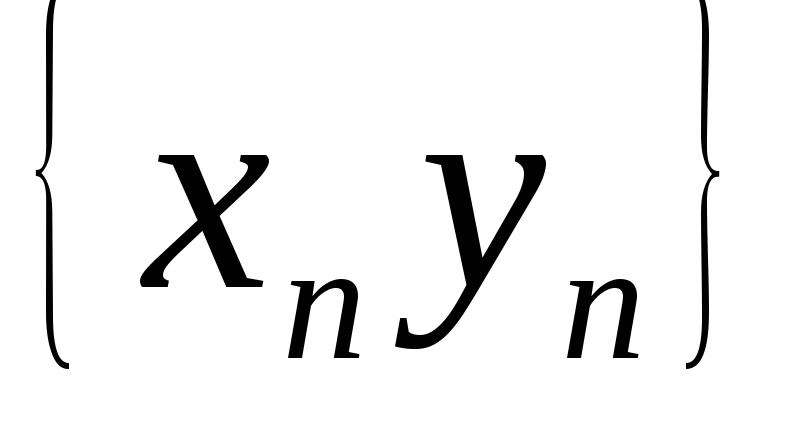
а) є збіжною при а = 0;
б) може бути збіжною тільки при а = 0;
в) завжди є розбіжною;
г) може бути збіжною також при а ≠ 0;
Ключ до тестових завдань (частина 2)
|
1б |
2б |
3а |
4б |
5а |
6а |
7в |
8г |
9а |
10г |
|
11б |
12а |
13г |
14а |
15г |
16г |
17г |
18г |
19а |
20б |
|
21в |
22а |
23г |
24б |
25б |
26б |
27г |
28г |
29б |
30в |
|
31б |
32г |
33б |
34б |
35г |
36в |
37б |
38б |
39а |
40г |
|
41в |
42а |
43б |
|
|
|
|
|
|
|
-
Інструктаж до виконання практичного завдання.
Методичні вказівки.
Визначення границі послідовності:
Конечна чи нескінченно віддалена точка числової прямої називається границею числової послідовності дійсних чисел, якщо, яка б ні була окрестність точки а, вона вміщує всі члени розглянутої послідовності, починаючи з деякого номера.
![]() чи
чи
![]() .
.
Якщо числова послідовність має скінчену границю, то вона називається збіжною послідовністю.
Ознаки існування границі числової послідовності:
1) Якщо
![]()
![]() .
.
2) Якщо
![]() ,
виконано, що
,
виконано, що
![]() та
та
![]() і
і
![]() ,
то
,
то
![]() .
.
3) Якщо числова послідовність має скінчену границю, то вона обмежена.
4) Будь – яка зростаюча
числова послідовність{х![]() }
має границю: скінчену, якщо вона обмежена
зверху, та нескінчену, якщо вона необмежена
зверху, причому
}
має границю: скінчену, якщо вона обмежена
зверху, та нескінчену, якщо вона необмежена
зверху, причому
![]() =
sup{х
=
sup{х![]() }.(Аналогічно
теорема формулюється для монотонно
спадаючої послідовності.)
}.(Аналогічно
теорема формулюється для монотонно
спадаючої послідовності.)
5) Для того, щоб
послідовність мала скінчену границю,
необхідно та достатньо, щоб вона
задовольняла умові Коші:
![]() .
.
Основні теореми про границю числової послідовності.
-
Якщо послідовність {х
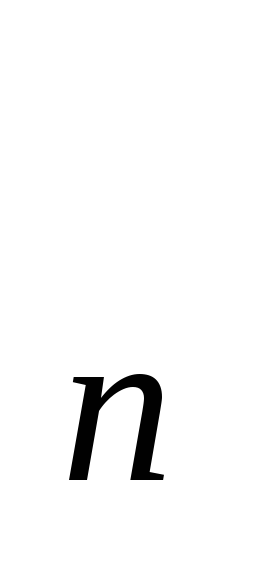 }
збігається, то збігається й послідовність
{|х
}
збігається, то збігається й послідовність
{|х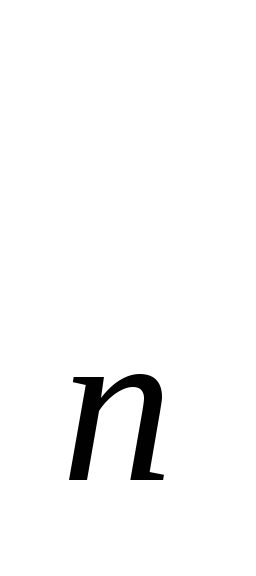 |},
причому якщо
|},
причому якщо
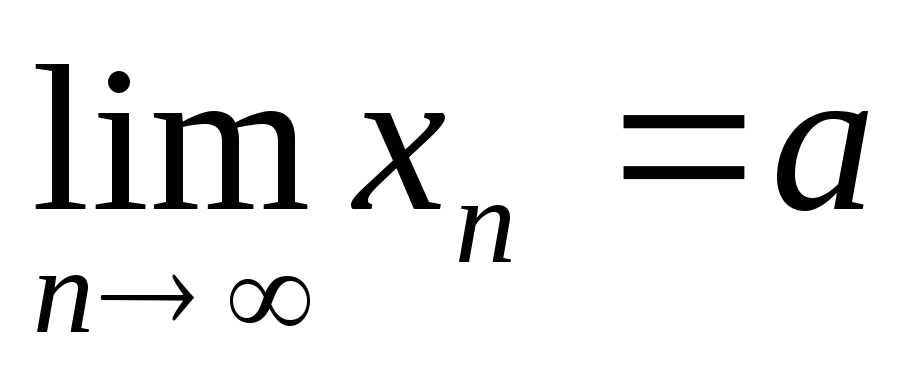 ,
то
,
то
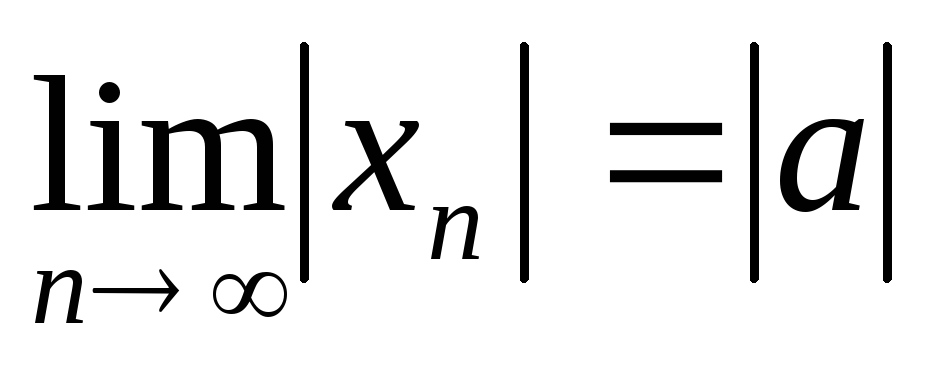 .
. -
Скінчена лінійна комбінація збіжних послідовностей також є збіжною послідовністю, причому її границя дорівнює лінійної комбінації границь даних послідовностей. Якщо
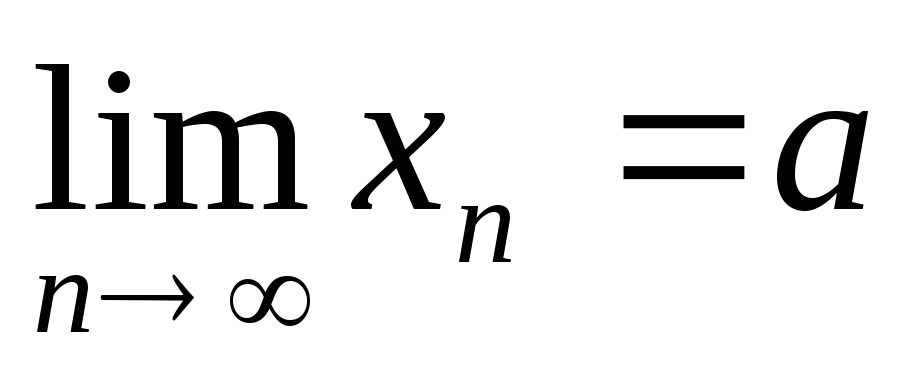 ,
,
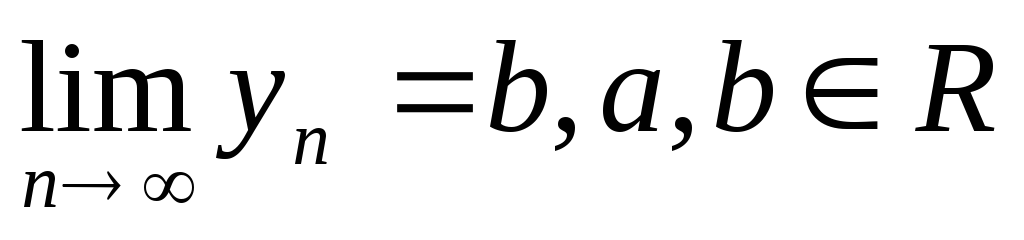 ,
та λ, μ – деякі числа, то
,
та λ, μ – деякі числа, то
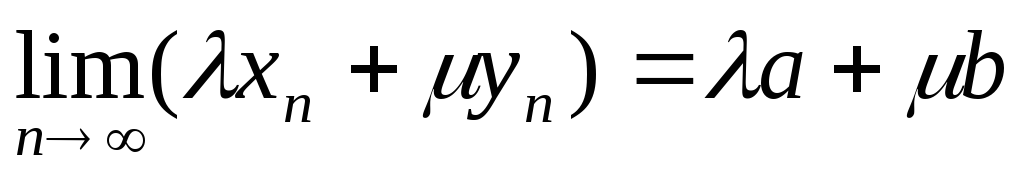 чи
чи
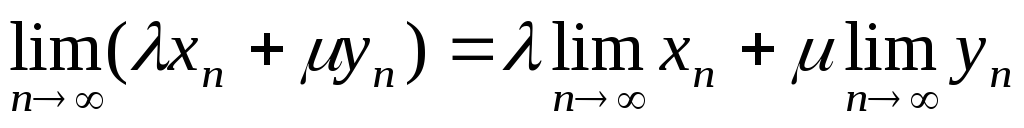 .
. -
Якщо послідовності {х
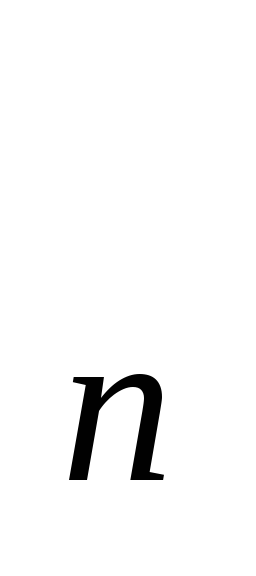 }
та {у
}
та {у }
збігаються, то їх добуток {х
}
збігаються, то їх добуток {х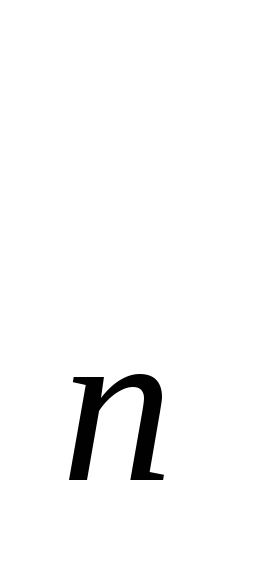 у
у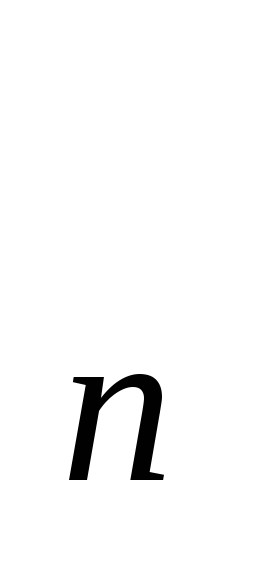 }
також збігається, причому
}
також збігається, причому
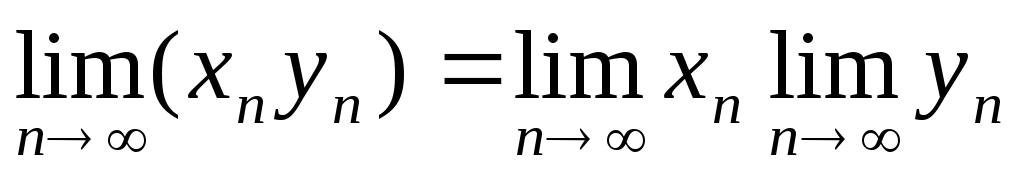 .
Тобто, границя добутку збіжних
послідовностей існує та дорівнює
добутку границь даних послідовностей.
.
Тобто, границя добутку збіжних
послідовностей існує та дорівнює
добутку границь даних послідовностей.
-
Якщо послідовність {х
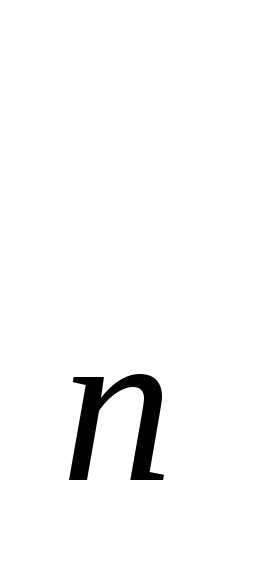 }
збігається та m – натуральне число,
то
}
збігається та m – натуральне число,
то
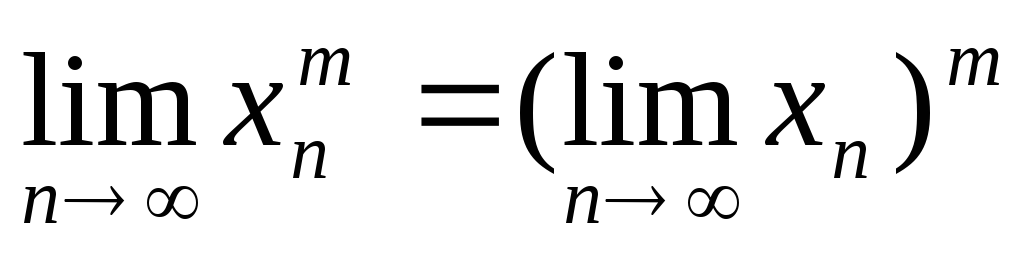 .
. -
Якщо послідовності {х
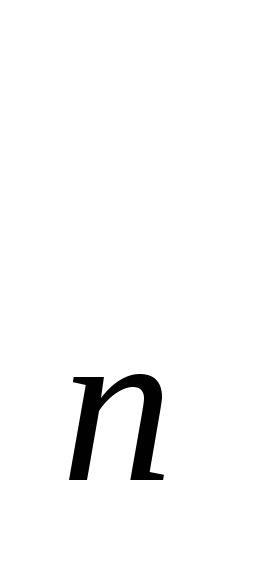 }
та {у
}
та {у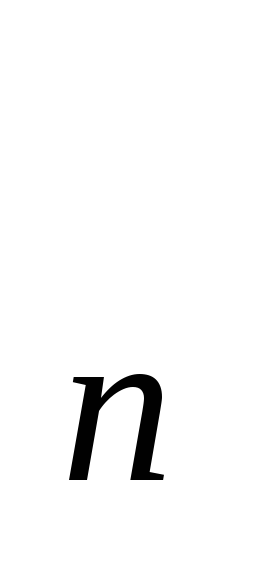 }
збігаються, та для всіх номерів n
виконується нерівність у
}
збігаються, та для всіх номерів n
виконується нерівність у ≠
0,
≠
0,
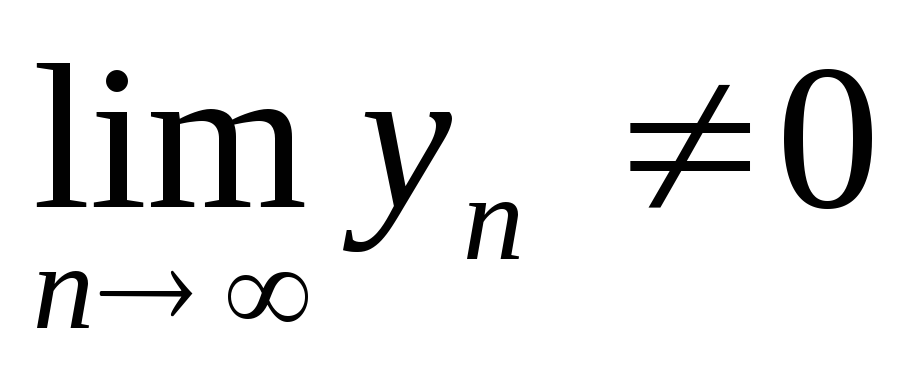 ,
то послідовність {х
,
то послідовність {х /
у
/
у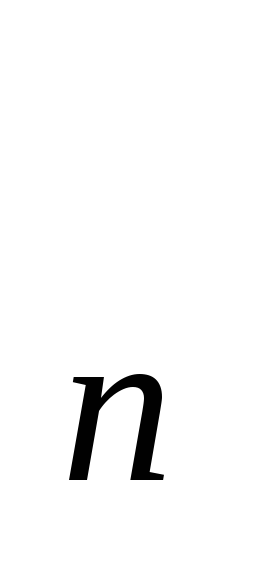 }
– збігається, причому
}
– збігається, причому
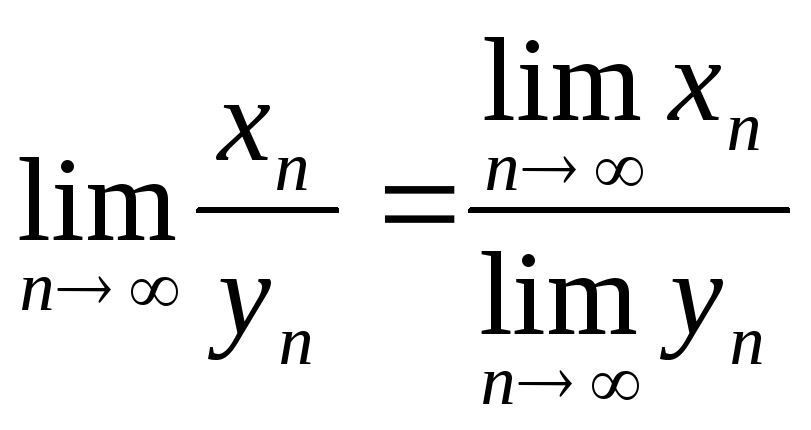 .
. -
Якщо
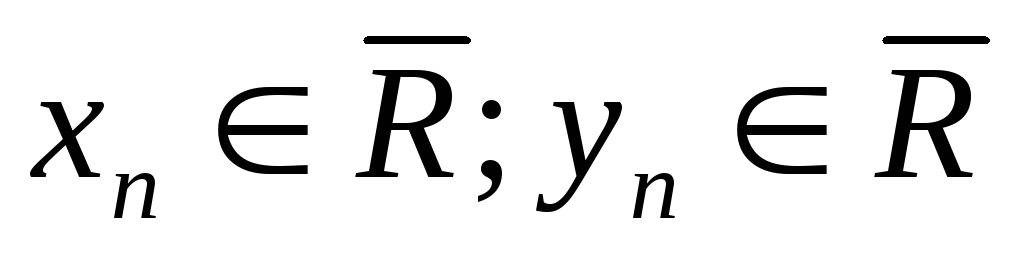 ,
,
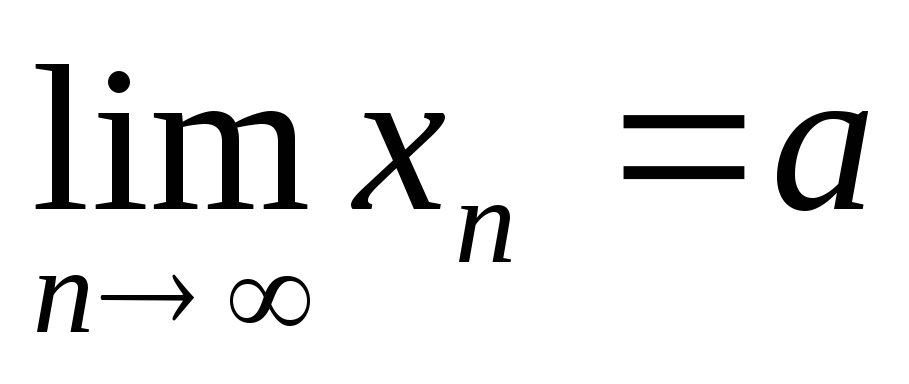 та
та
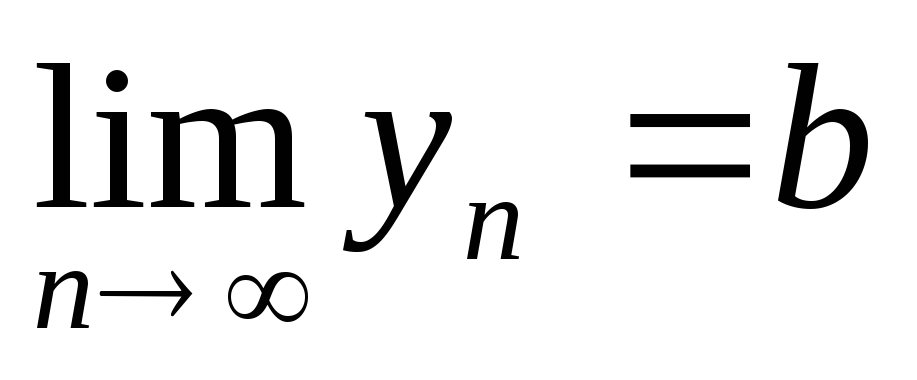 і a < b, a, b
і a < b, a, b
 R, то
R, то
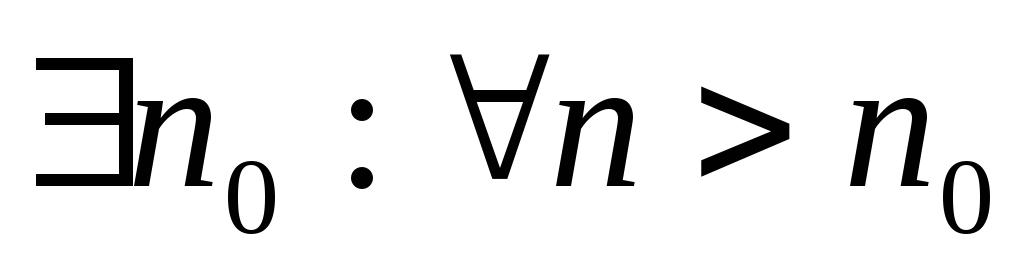 виконано, що х
виконано, що х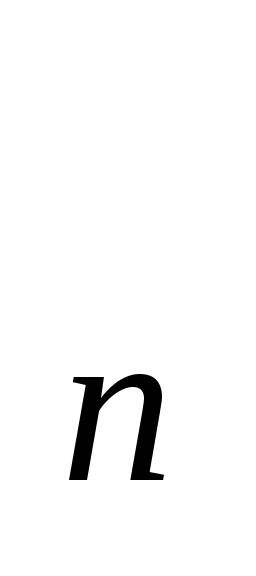 <
y
<
y .
. -
 ,
де е ≈ 2,718281828459045 (експонента).
,
де е ≈ 2,718281828459045 (експонента).
Нескінченно малі та великі послідовності.
Числова послідовність, границя якої дорівнює 0, називається нескінченно малою.
Якщо границя числової
послідовності нескінчена, тобто
![]() ,
то
,
то
![]() .
.
![]()
![]() ;
;
![]()
![]() ;
;
Послідовність, границею якої є ∞, називається нескінченно великою.
Гранична точка.
З будь – якої обмеженої числової послідовності можна виділити збіжну підпослідовність, а з будь – якої необмеженої зверху(знизу) числової послідовності – підпослідовність, що має своєю границею +∞(- ∞).(теорема Больцано – Веєрштрасса.)
Границя, скінчена чи деякого знаку нескінчена, підпослідовності числової послідовності називається частковою границею цієї послідовності.
Будь – яка числова послідовність завжди має хоча б одну часткову границю (скінчену чи нескінчену).
Найменша часткова границя
послідовності х![]()
![]() називається нижньою границею, найбільша
часткова границя послідовності х
називається нижньою границею, найбільша
часткова границя послідовності х![]()
![]() називається верхньою границею цієї
послідовності.
називається верхньою границею цієї
послідовності.
Рівність
![]() =
=
![]() є необхідною та достатньою умовою
існування границі послідовності х
є необхідною та достатньою умовою
існування границі послідовності х![]() .
.
Приклади.
-
Знайти границю послідовності:
 .
. -
Довести рівність:
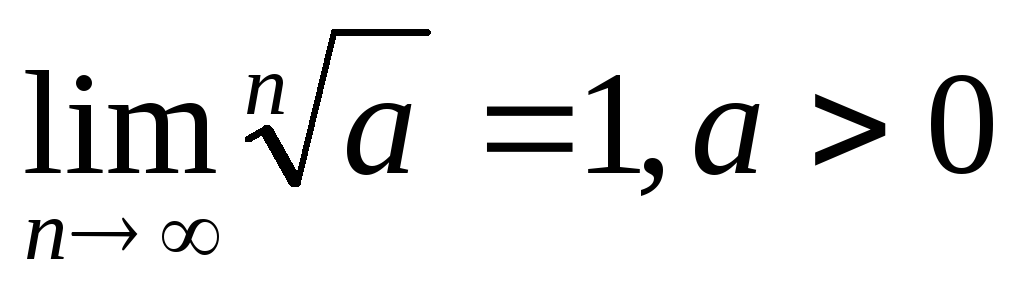 .
.
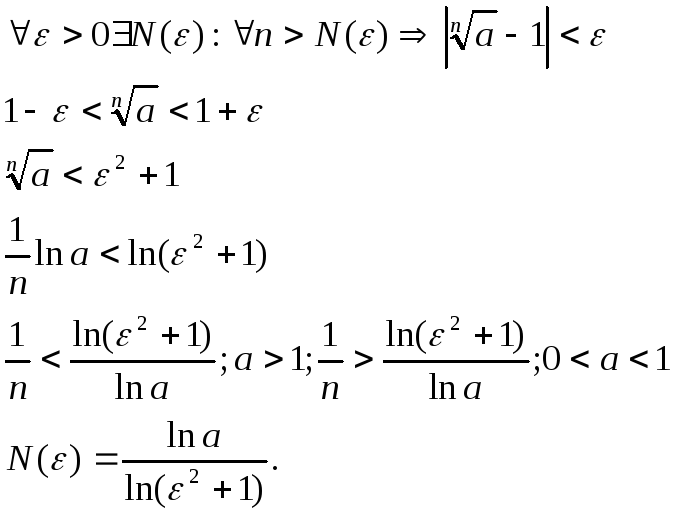
-
Для послідовності х
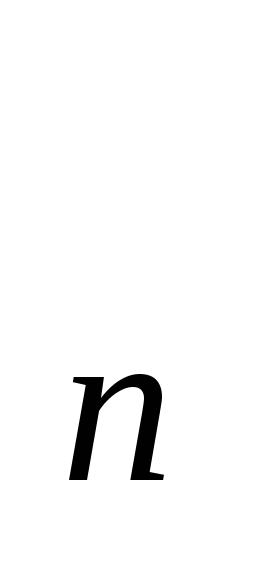 =
(-1)
=
(-1) (2+3/n),
(n = 1,2,3,….) знайти inf х
(2+3/n),
(n = 1,2,3,….) знайти inf х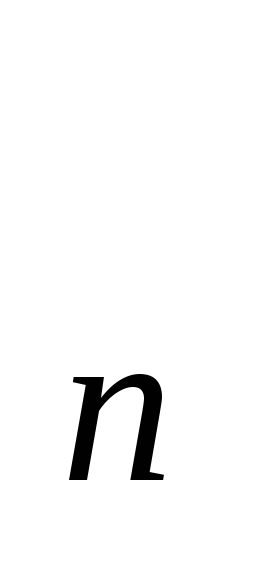 ,
sup х
,
sup х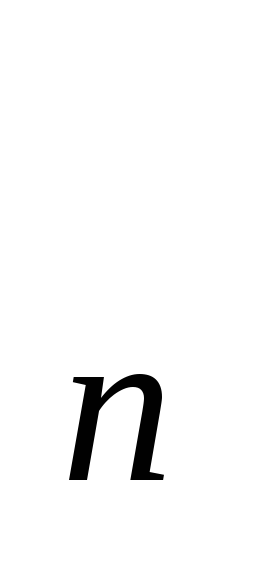 ,
,
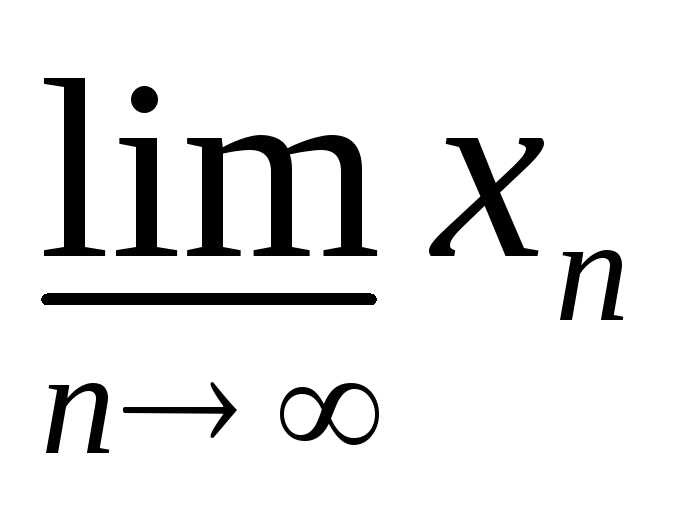 ,
,
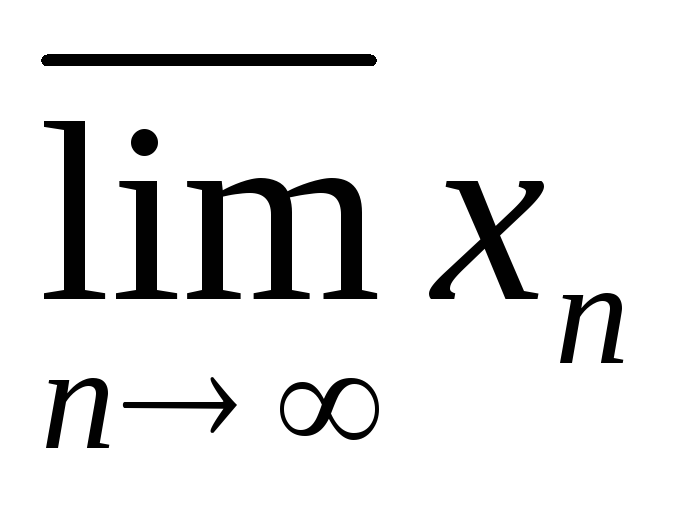 .
.
Якщо n
– непарне, то х![]() =
- (2+3/(2k-1)), k = 1,2,3,…… Тому: inf х
=
- (2+3/(2k-1)), k = 1,2,3,…… Тому: inf х![]() = -5,
= -5,
![]() =
-2.
=
-2.
Якщо n
–парне, то х![]() =
(2+3/(2k)), k = 1,2,3,…; sup х
=
(2+3/(2k)), k = 1,2,3,…; sup х![]() = 7/2,
= 7/2,
![]() = 2.
= 2.
-
Виконати практичне завдання.
Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989. – Т. 1.
Стор.
136, №№ 1, 2.

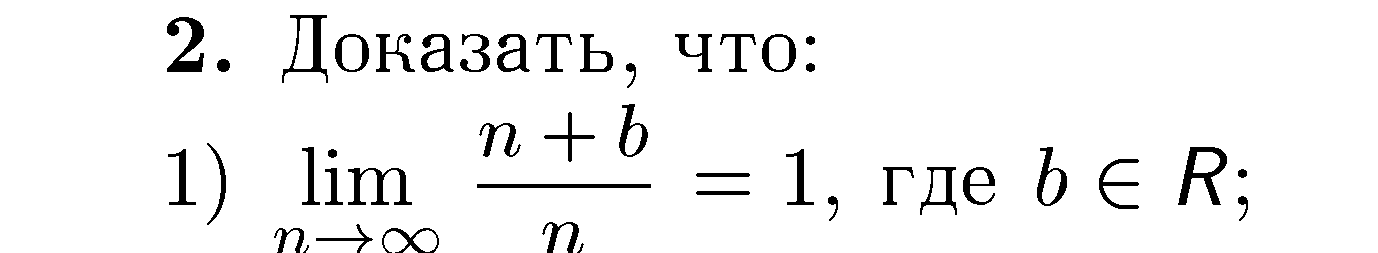
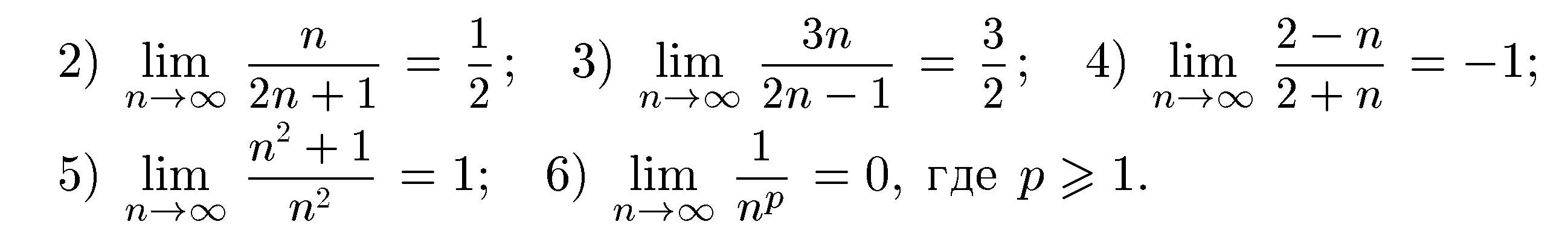
Стор. 138, № 13.
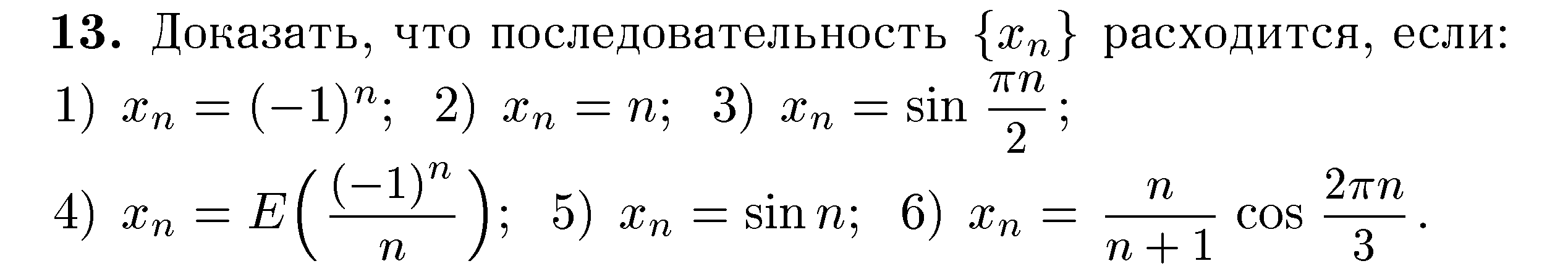
Стор. 138, №№ 18, 19.

Домашнє завдання:
-
Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989. – Т. 1., стор. 138, №№ 15, 19;
-
Тестові завдання – розібрати частину 2, частину 3
