Варіант 4.

1. Визначити кількість точок х0, в яких границя не існує.

а) 4;

б) 1;

в) 0;

г) 2;

2. дорівнює

а) не існує;

б) 5;

в) 1;

г) 0;

3. Нехай . Тоді:

а) для довільного c;

б) ніколи ( таких с не існує);

в) якщо с = 0;

г) якщо с = 1;

4. Функція неперервна на відрізку і на його кінцях приймає значення різних знаків. Тоді на цьому відрізку функція

а) диференційована;

б) монотонна;

в) обертається в нуль;

г) не обертається в нуль;

5. При х → ∞ , х + sin х ~ f(х), якщо f(х) = :

а) х ²;

б) х;

в) ;

г) е;

6. Нехай f(х) =О(g(х)) при х → а. Тоді

а) f(х)g(х) =о(1) при х → а;

б) f ≈ g при х → а;

в) g(х) =о(f(х)) при х → а;

г) ;

7. Нехай f(х) задана на проміжку (a; b). Яке твердження правильне?

а) якщо f(х) не має нулів в (a; b), то вона знакопостійна в ньому;

б) якщо f(х) неперервна в (a; b), то вона обмежена в ньому;

в) якщо f(х) неперервна в (a; b) і (a; b), де f(х0) = 0, то знайдуться такі х1 та х2, що f(х1) · f(х2) < 0;

г) якщо f(х) неперервна в (a; b) і не має нулів в (a; b), то вона знакопостійна;

8. Якщо існує , то :

а) f визначена в точці х0;

б) f неперервна в точці х0;

в) f має розрив в точці х0;

г) f обмежена в деякому проколотому околі точки х0;

9. Нехай f(х) → 0 при х → a. Тоді:

а) sin f(х) ~ ln f(х) при х → a;

б) sin f(х) ~ tg f(х) при х → a;

в) sin f(х) ~ eпри х → a;

г) sin f(х) ~ cos f(х) при х → a;

10. Яка з рівностей вірна?

а) ;

б) ;

в) ;

г) ;

Ключ до тестових завдань.

варіант	1	2	3	4	5	6	7	8	9	10
1	г	г	а	в	г	а	г	а	г	б
2	б	б	г	б	а	в	г	а	г	а
3	б	б	а	г	а	в	г	г	а	г
4	б	б	г	в	б	г	г	г	б	в

2. Інструктаж до виконання практичної роботи.

Методичні рекомендації:

Неперервність функції.

Нехай функція y = f(x) визначена на множині X і нехай крапка х₀ Є Х є граничною крапкою цієї множини. Говорять, що функція f(х) неперервна в крапці х₀, якщо . Остання умова рівносильна умові.

Функція f(x) неперервна в крапці х₀ тоді й тільки тоді, коли f(х₀ – 0) = f(х₀ + 0) = f(х₀).

Функція f(х) неперервна на множині X, якщо вона неперервна в кожній крапці цієї множини.

Крапки розриву першого роду.

Нехай крапка х₀ є граничною крапкою області визначення X функції f(x). Крапка х₀ називається крапкою розриву першого роду функції f(x), якщо межі праворуч і ліворуч кінцеві. Якщо при цьому f(х₀ – 0) = f(х₀ + 0) ≠ f(х₀), то х₀ – крапка переборного розриву; якщо f(х₀ – 0) ≠ f(х₀ + 0), то х₀ – крапка непереборного розриву першого роду, а різниця f(х₀ – 0) – f(х₀ + 0) називається стрибком функції f(х) у крапці х₀.

Крапки розриву другого роду.

Якщо хоча б одна з меж f(х₀ – 0) і f(х₀ + 0) не існує або нескінченна, то крапка х₀ називається крапкою розриву другого роду функції f(x).

Приклади розв’язання практичних завдань:

Приклад № 1.

Використовуючи лише визначення, довести неперервність функції , при будь-якому значенніх.

Рішення.

Нехай х₀ – довільна крапка числовий вісі. Спочатку обчислюємо :

.

Потім обчислюємо значення функції в крапці х₀ :

.

Порівнюючи отримані результати, бачимо, що: .

Отже, функція f(x) неперервна у крапці х₀, опираючись на визначення безперервності. Оскільки крапка х₀ – довільна крапка числовий вісі, доведена неперервність функції для всіх значень х.

Приклад № 2.

Дані функції:

а).

б).

Знайти крапки розриву, якщо вони існують. Визначити стрибки функцій у крапках, де є розриви першого роду.

Рішення.

а). Область визначення функції – вся числова вісь (– ∞, ∞). На інтервалах (– ∞, 1), (1, 3), (3, ∞) функція неперервна. Тому розриви можливі лише в крапках х = 1, х = 3, у яких змінюється аналітичне завдання функції.

Знайдемо однобічні межі функції в крапці х = 1:

Значення функції в крапці х = 1 визначається першим аналітичним вираженням, тобто . Тому що, то в крапціх = 1 функція неперервна.

Розглянемо крапку х = 3:

Ми бачимо, що права й ліва межі, хоча й кінцеві, але не рівні між собою, тому в крапці х=3 функція має розрив першого роду.

Стрибок функції в крапці розриву.

б). Функція визначена й неперервна па всієї числової вісі, крім крапки х = 3/2. Тому що 2x – 3 > 0 при x > 3/2 і 2x – 3 < 0 при x< 3/2, то

Отже, .

Тому в крапці х = 3/2 функція має кінцевий розрив першого роду. Стрибок функції в цій крапці дорівнює 1– (– 1) = 2.

3. Виконати практичне завдання.

Дослідити неперервність функцій:

а).

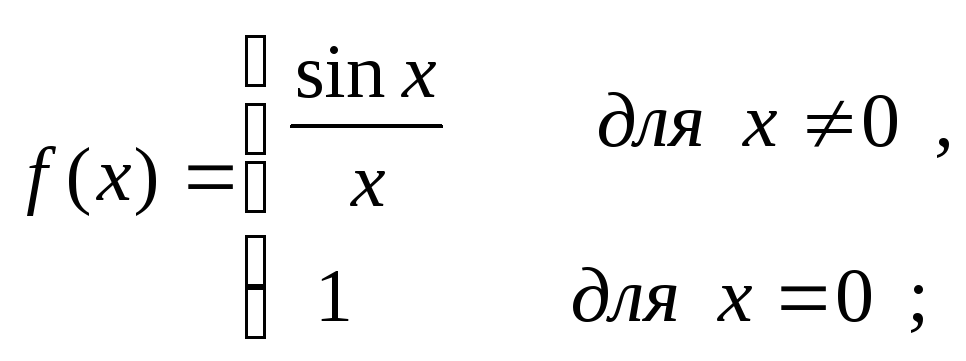
б).

в).

г).