ВАШ КОРР КУРС Геометрия Ковал Лосева

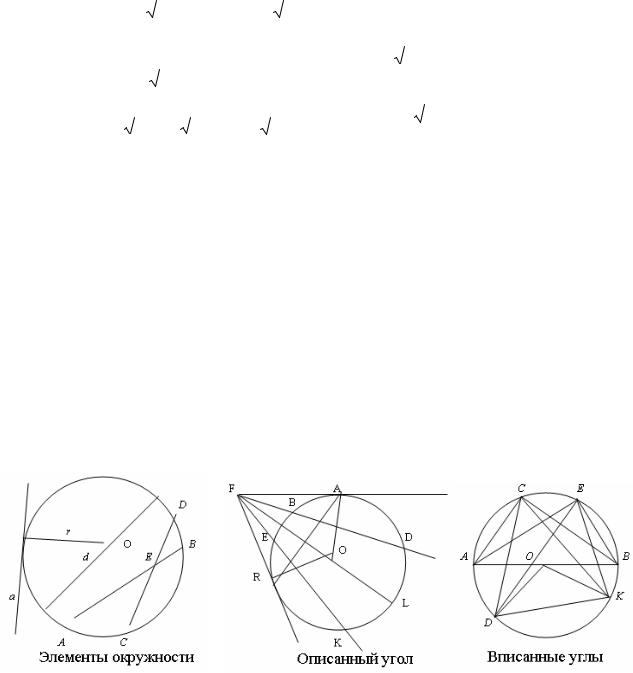
Два правильных многоугольника с одинаковым числом сторон подобны,

Окружность – фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки, называемой центром окружности.

r – радиус окружности, d – диаметр окружности, d=2r; а – касательная к

ÐACB, ÐАЕВ – углы, опирающиеся на диаметр окружности, ÐАСВ = ÐАЕВ = 90o . ÐDCK, DEK – углы, вписанные в окружность и опирающиеся на общую хорду DK, ÐDCK = ÐDEK ; ÐDOK – центральный угол окружности, опирающийся на хорду

DK, ÐDCK = ÐDEK = 12 ÐDOK = ÈDK .

20

Задача 9. Диагонали ромба относятся как 3:4. Вычислите площадь ромба, если длина вписанной в ромб окружности равна 24π см.

Указание: выразите значение площади через диагонали ромба; рассмотрите высоту ромба как диаметр окружности.

Ответ: 600 см2.

Задача 10. Около окружности описана трапеция, периметр которой равен 20 см. Найдите среднюю линию трапеции.

Указание: воспользуйтесь свойством сторон четырёхугольника, в который вписана окружность.

Ответ: 5 см.

ІІ. Продвинутый уровень сложности

Задача 1. Основания трапеции а и b (a < b). Прямая, которая пересекает боковые стороны трапеции в точках M и N, проходит через точку пересечения диагоналей параллельно основаниям. Найдите длину отрезка MN.

Указание: рассмотрите треугольники, проведите в них высоты; используйте подобие треугольников.

2ab

Ответ: a + b .

Задача 2. Выпуклый четырёхугольник разделён диагоналями на четыре треугольника; площади трёх из них равны 10, 20 и 30 см2, и каждая меньше площади четвёртого треугольника. Найдите площадь данного четырёхугольника.

Указание: выразите площади треугольников, перемножьте полученные равенства, выполните преобразования.

Ответ: 120 см2.

Задача 3. В прямоугольнике со сторонами а и b проведены биссектрисы всех углов до взаимного пересечения. Найдите площадь четырёхугольника, образованного биссектрисами.

Указание: рассмотрите прямоугольные треугольники.

Ответ: (b − a ) 2 .

2

Задача 4. В ромб вписана окружность радиуса R. Найдите площадь ромба, если его большая диагональ в 4 раза больше радиуса вписанной окружности.

Указание: проведите радиус в точку касания, рассмотрите прямоугольные треугольники.

Ответ: 8 R 2 3 .

3

Задача 5. Диагонали трапеции разбивают её на четыре треугольника. Докажите, что если площади двух из них, прилежащих к основаниям трапеции, равны p2 и q2, то площадь трапеции равна (p + q)2.

Указание: рассмотрите равные и подобные треугольники.

Задача 6. В окружность вписан четырёхугольник, длины сторон которого равны a, b, c, d. Вычислите отношение длин диагоналей этого четырёхугольника.

Указание: используйте теорему синусов, её следствие.

Ответ: ad + bc ab + cd

22

Задача 7. В выпуклом четырёхугольнике ABCD биссектрисы углов А и В пересекаются в точке О. Докажите, что угол между биссектрисами этих углов равен полусумме углов С и D (ÐC+ÐD<180º).

Указание: воспользуйтесь теоремами о сумме углов треугольника, четырёхугольника.

Задача 8. Окружность с центром О касается сторон МК, КТ и ТМ ∆МКТ в точках А, В и С соответственно. Найдите углы ∆АВС, если ÐМКТ=42º, ÐКМТ=82º. Указание: рассмотрите четырёхугольники МАОС, АКВО, вписанные и центральные углы.

Ответ: 49º; 69º; 62º.

Задача 9. Из точки А к окружности диаметром ВС проведена касательная АС. Отрезок АВ пересекается с окружностью в точке В, AD=2 см, BD=6 см. Найдите градусную меру дуги окружности, заключённой внутри ∆АВС.

Указание: рассмотрите прямоугольный треугольник; проведите высоту из вершины прямого угла; используйте соотношения между сторонами и углами в треугольнике.

Ответ: 60º.

Задача 10. Даны две окружности. Вторая окружность имеет центр О на первой окружности и касается её диаметра АВ в точке М. Найдите длину второй окружности, если АМ=т, ВМ=п.

Указание: проведите ОА, ОМ, ОВ; рассмотрите прямоугольный треугольник.

Ответ: 2π mn .

3. Задания для самоконтроля

1. Основания трапеции а и b (a<b). Найдите длину отрезка, параллельного основаниям, который делит площадь трапеции пополам.

Указание: проведите перпендикуляр из точки С на отрезок MN и из точки N на основание АD; из вершины С проведите отрезок, параллельный боковой стороне трапеции; рассмотрите треугольники.

Ответ: a2 + b2 .

2

2.Найдите площадь трапеции с основаниями 6 и 7 см и диагоналями 5 и 12 см. Указание: проведите через вершину трапеции прямую, параллельную боковой

стороне; рассмотрите полученный треугольник.

Ответ: 30 см2.

3.Дан квадрат ABCD со стороной а. Найдите радиус окружности, проходящей через

середину стороны АВ, центр квадрата и вершину С.

Указание: найдите одну сторону треугольника и синус противолежащего угла.

Ответ: a410 .

4. Точка касания вписанной в ромб окружности делит его стороны на отрезки, разность которых 10 см. Найдите площадь ромба, если длина окружности равняется 24π см.

23

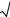
Указание: рассмотрите высоту ромба, являющуюся диаметром вписанной окружности и проходящую через точки касания; рассмотрите один из четырёх треугольников, на которые делят ромб его диагонали.

Ответ: 624 см2.

5. Из вершины тупого угла ромба ABCD опущены перпендикуляры ВЕ и ВF на стороны AD и DC, пересекающие диагональ АС в точках M и N. Точка Е соединена с F. Определите площадь фигуры MNFE, если диагонали ромба равны 160 и 120 см.

Указание: рассмотрите подобные треугольники, используйте отношения сторон, теорему Пифагора.

Ответ: 1723,68 см2.

6. В параллелограмме со сторонами a и b и углом α проведены биссектрисы четырёх углов. Найдите площадь четырёхугольника, ограниченного биссектрисами.

Указание: докажите, что полученный четырёхугольник прямоугольный; рассмотрите треугольники.

диагоналями напротив основания равен 120º. Найдите диагонали трапеции. Указание: через одну из вершин трапеции проведите прямую, параллельную

диагонали до пересечения с продолжением основания; воспользуйтесь теоремой косинусов и формулой площади треугольника; решите систему уравнений.

Ответ: 6 см и 10 см.

8. Биссектриса, проведенная из вершины прямоугольника, делит его диагональ на отрезки 15 см и 20 см. Найдите площадь прямоугольника.

Указание: рассмотрите подобные треугольники, равнобедренный треугольник, используйте теорему Пифагора.

Ответ: 588 см2.

9. Из точки А окружности проведены диаметр АВ и хорда АС, которая продолжена за С на расстояние СК, равное АС. Найдите ВС, если КВ=10 см, ÐСАВ=30º.

Указание: рассмотрите вписанный угол, опирающийся на диаметр; используйте свойства равнобедренного треугольника; проведите медиану во вписанном треугольнике, рассмотрите равносторонний треугольник.

Ответ: 5 см.

10. В окружности хорда СЕ перпендикулярна диаметру АВ, К – точка их пересечения. Найдите радиус окружности, если КВ=1 см, СК=3 см.

Указание: рассмотрите угол, опирающийся на диаметр; используйте свойство высоты, проведённой из вершины прямого угла.

Ответ: 5 см.

24

Занятие № 4

Тема занятия: «Метод координат на плоскости»

Цели:

-обобщить и углубить школьные знания студентов об уравнениях плоских кривых;

-познакомить с различными системами координат на плоскости;

-сформировать навыки применения метода координат на плоскости при решении геометрических задач.

1. Краткое содержание теоретического материала

1. Расстояние между точками. Вычисление длины отрезка

На плоскости даны две точки А(х1;у1 ) и В(х1;у1). Расстояние АВ между точками

вычисляется по формуле АВ = (х2 − х1 )2 + (у2 − у1 )2 .

В частности, расстояние точки М(х;у) от начала координат определяется по формуле

ОМ = х2 + у2 .

2. Деление отрезка в данном отношении.

Если даны две точки А(х1;у1 ) и В(х 2 ;у 2 ), то координаты всякой третьей точки С,

3. Уравнение прямой.

Уравнение прямой с угловым коэффициентом:

Всякая прямая, не параллельная оси у, представляется уравнением вида у=kх+b. Параметр k характеризует направление прямой и называется ее угловым коэффициентом. k = tgϕ , где ϕ - угол, образованный прямой с положительным

направлением оси абсцисс.

Прямая, параллельная оси у, представляется уравнением вида у=а.

Если две прямые параллельны, то угловые коэффициенты этих прямых равны: k=k1 .

Если две прямые перпендикулярны, то: k1 = − 1k .

Уравнение прямой, заданной двумя точками.

Угловой коэффициент этой прямой вычисляется по формуле: k = y2 − y1 . x2 − x1

25

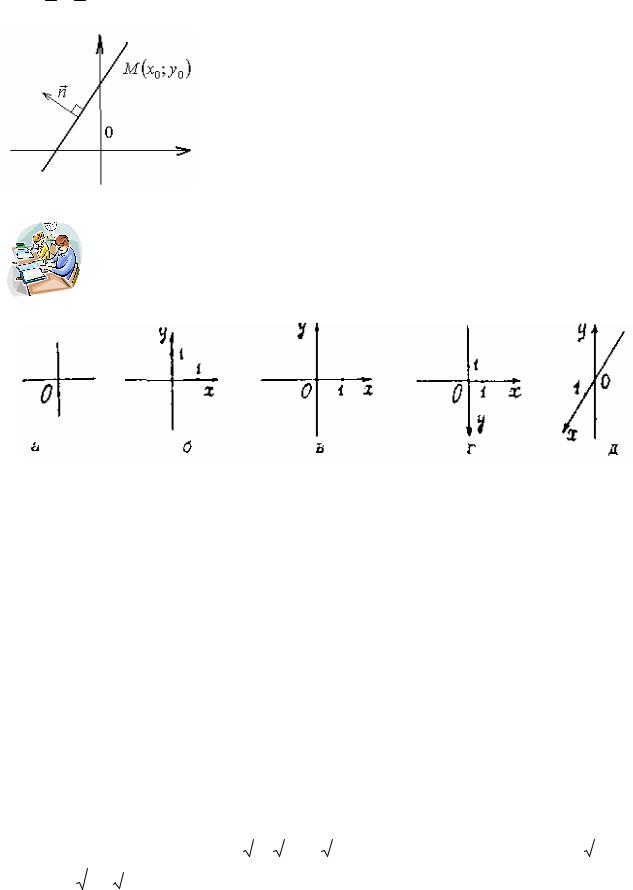
Если данные точки А и В лежат на осях координат, то уравнение прямой примет вид: ах + bу = 1, которое называется уравнением прямой в отрезках.

Любой ненулевой вектор n = (a;b), перпендикулярный прямой, называется нормалью прямой. Точка М(х 0 ;у 0 )

принадлежит прямой, тогда уравнение прямой запишется в виде: a(x − x0 )+ b(y − y0 )= 0 .

Общее уравнение прямой имеет вид: ах+by+c=0, где а и b одновременно не равны нулю.

4. Уравнение окружности

Окружность радиусом R с центром в точке С(a;b) записывается уравнением: (х - а)2 + (у - b)2 = R2 .

2. Система задач для аудиторных занатий

Задача 1. На каком рисунке правильно задана система декартовых координат?

Указание: воспользуйтесь определением прямоугольной системы координат. Задача 2. Постройте точки по данным координатам, соедините их отрезками и определите вид образованной фигуры: 1) А(3;2), В(-3;2), С(-3;-2), Д(3;-2); 2) О(0;0), М(-4;0), К(-4;-4), Д(0;-4); 3) А(0;5), В(-2;0), О(0;0), С(2;0).

Ответ: 1) квадрат; 2) квадрат; 3) равнобедренный треугольник.

Задача 3. Постройте равнобедренный треугольник АВС, если В(1;−5), а

основание АС лежит на оси ординат и имеет длину, равную 4 единицам. Задача 4. а) Даны точки А(-6;-4) и В(2;у). Как при изменении ординаты точки В в пределах от -3 до 4 будет изменяться длина отрезка АВ?

б) Даны точки С(х; 1) и Д(3; 7). Как при изменении абсциссы точки С будет меняться длина отрезка СД? При каком значении х она минимальна?

Задача 5. Определите вид четырехугольника АВСД, если его вершины имеют координаты: А(-3;-4), В(-1;-1), С(2;1), Д(0;-2).

Ответ:ромб.

Задача 6. Найдите длины диагоналей, периметр и площадь: а) прямоугольника АВСД,

26

Задача 7. Составьте уравнение прямой:

1)которая параллельна оси ОX и равноудалена от начала координат на расстояние 6 единиц;

2)которая параллельна прямой y = 2 и равноудалена от нее на 3 ед.;

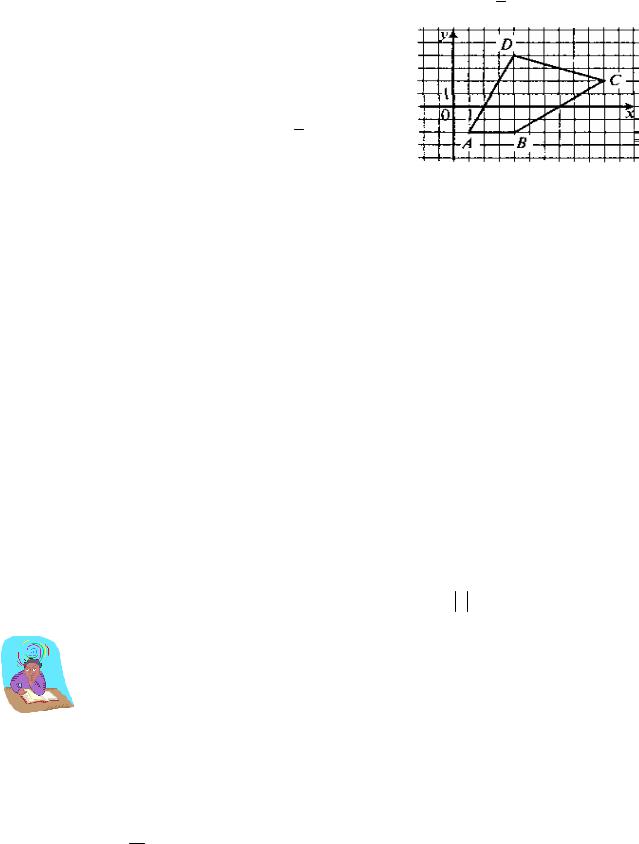
Задача 8. Используя рисунок запишите уравнения прямых, содержащих стороны и диагонали четырехугольника АВСD.

Задача 9. Какая из данных прямых лишняя и почему?

а) y = −3x; y − 4x =1; y = x; y = 6x; y + 5x = 0;

4x − y = 3 .

Задача 10. Прямая задана уравнением y = kx + l . Какой угловой коэффициент будет

у прямой?

Задача 11. Прямая а задается уравнением у=4х+1. Какие из данных прямых

Задача 12. Определите вид четырехугольника, стороны которого лежат на прямых, заданных уравнениями: y = x +1; y = 3; y =1 − x; y = x + 3.

Ответ: трапеция.

Задача 13. Точки M и N являются соответственно серединами сторон АВ и АС треугольника AВС. Расстояние от вершины А до противолежащей стороны равно 4. Какое уравнение имеет прямая ВС, если прямая МN задается уравнением y + 2 = 0 ?

Сколько решений имеет задача? Ответ: 2 решения.

Задача 14. Окружность с центром (3;5) касается оси абсцисс. В каких точках она пересекает ось ординат?

Задача 15. Окружность имеет уравнение (х − 3)2 + (у +1)2 = 25 . Определите длины хорд окружности, которые лежат на осях координат.

Задача 16. Докажите, что окружность х2 + у2 + 2ах +1 = 0, а > 1, не пересекается с осью у.

3. Задания для самоконтроля

1.Точки А(3;2) и В(а;-1) лежат на одной прямой, параллельной оси Оу. Найдите а.

Ответ: 3.

2.Три вершины параллелограмма находятся в точках (3;2), (2;5), (8;7). Найдите координаты четвертой вершины.

Ответ: (9;4)

3.Вершины треугольника – точки (0;0), (6,4), (10;26). Определите длины его медиан.

Ответ: 25, 17, 82.

27

4. Какие из точек А(5;1), В(6;5), С(6;6), D(-6;-2) лежат на окружности

(х + 2)2 + (у − 5)2 = 65?

Ответ: А, С, D.

5. Найдите периметр треугольника, ограниченного осями координат и прямой, имеющей уравнение 5х-12у-120=0.

Ответ: 60.

6.Вершины треугольника находятся в точках А(0;13), В(2;-1), С(10;3). Докажите, что его медианы ВD и СЕ взаимно перпендикулярны.

7.В каких точках биссектриса первой четверти (или ее продолжение) пересекает

окружность (х − 2)2 + (у −1)2 = 25?

Ответ: (5;5), (-3;-3).

Занятие № 5 (6)

Тема занятия: «Прямые и плоскости в пространстве»

(2 часа для студентов специальности «Математика», «Статистика».

4 часа для студентов специальности «Прикладная математика», «Информатика») Цели:

-обобщить и систематизировать школьные знания студентов о прямых, плоскостях и их взаимных расположениях;

-сформировать умения студентов находить углы между прямой и плоскостью, между плоскостями;

-закрепить и осознать понятия общего перпендикуляра двух скрещивающихся прямых, расстояния между двумя скрещивающимися прямыми, угла между ними.

1. Краткое содержание теоретического материала

1.1 О существовании плоскости.

1.Две прямые, которые пересекаются, определяют в пространстве плоскость, и притом только одну (одна из аксиом).

2.Через прямую и точку, которая не принадлежит ей, можно провести плоскость, и притом только одну (теорема).

3.Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну (теорема).

28

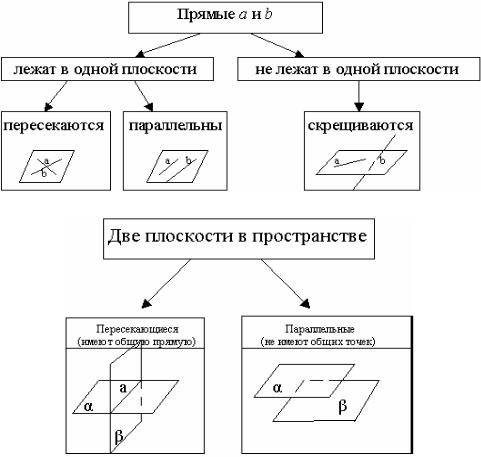
1.2 Взаимное размещение двух прямых в пространстве.

1.3 Взаимное размещение двух плоскостей.

1.4 Параллельное проектирование Теорема. Если проектируемые отрезки не параллельны проектирующей прямой, то при параллельном проектировании:

1)отрезки изображаются отрезками;

2)параллельные отрезки изображаются параллельными отрезками или отрезками одной прямой;

3)отношение длин параллельных отрезков и отрезков одной прямой сохраняется.

Изображение фигур

1. Изображение треугольника:

Любой треугольник может быть изображением треугольника произвольной формы, в частности: правильного, равнобедренного, прямоугольного.

2. Изображение параллелограмма:

Изображением параллелограмма (прямоугольника, ромба, квадрата) можно считать произвольный параллелограмм, принадлежащий плоскости проекций.

3. Изображение трапеции:

Изображением трапеции является трапеция, в которой отношение длин оснований изображения равно отношению длин оснований проектируемой трапеции.

4. Изображение четырехугольника:

Изображением произвольного четырехугольника (не параллелограмма и не трапеции) является произвольный четырехугольник.

29