
Metodichka_lab_Ekonometria
.pdfЛегко проверить, что если из выборки удалить два первых наблюдения y1, y2 , то по критерию µ гипотеза о гетероскедастичности
будет отвергнута так как в этом случае |
µ < χтабл2 |
. (5,17 < 5,99) . |
Модель, |
|||||
построенная |
по |
22 |
наблюдениям, |
будет |
иметь |
вид |
||
yˆ′ = − 4,61 + 0,31x1 + 5,12x4 −154,09x5 с |
коэффициентом |
детерминации |
||||||
R2 =96,3 % |
и средней |
относительной |
ошибкой |
аппроксимации |
||||
Eср.отн. = 3 % и будет удовлетворять условию гомоскедастичности.
Так как по критерию µ массив данных Y (24 наблюдения) признан гетероскедастичным (при уровне значимости α = 0,05 ), а ни одна из переменных X1, X 4 , X5 не является источником гетероскедастичности, то
можно предположить, что причиной гетероскедастичности являются факторы, не учтенные в модели (3-й случай – формула (4.30)). Также следует отметить, что если в тесте Гольфельда–Квандта по переменной X 4 , задать уровень значимости α = 0,1 то переменная X 4 будет признана
причиной гетероскедастичности остатков модели, так как в этом случае табличное значение F-статистики при уровне значимости α = 0,1 и
степенях свободы k1 = k2 = 6 |
равно Fтабл. (α = 0,05, |
k1 = 6,k2 = 6) = 3,005 и |
||
F (4) |
> F |
(3,14 > 3,005) . |
Следовательно, для |
оценки параметров |
факт. |
табл. |
|
|
|
следует использовать обобщённый МНК. Предположим, что дисперсия
остатков пропорциональна квадрату значений переменной |
X 4 (условие |
||
(4.29)). Тогда в матрице преобразований Ω (формула |
4.27, ячейки |
||
G2 : AD25 на рис. 4.14) λ = |
1 |
. Используем оператор оценивания (4.29) |
|
|
|||
i |
x2 |
|
|
i4
для оценки параметров ОМНК (рис. 4.13, 4.14).
Таблица 4.5
Реализация в MS Excel формул при расчете параметров модели ОМНК (рис. 4.13, 4.14)
Адрес ячейки |
|
Формула |
|
|
|
Реализация в MS Excel |
|||||||||
G2 : AD25 |
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
G2 = D2^2 |
|
AG2 : BD25 |
|
|
|
Ω−1 |
|
|
|
|
|
|
= МОБР(G2 : AD25) |
||||
B28:Y 31 |
|
Xтрансп. = X ′ |
|
|
= ТРАНСП(B2 : E25) |
||||||||||
B34 :Y 37 |
|
|
|
|
′ |
|
−1 |
|
|
|
|
= МУМНОЖ(B28 : Y31;AG2 : BD25) |
|||
|
|
|
X Ω |
|
|
|
|
|
|
|
|
|
|||
B40 : E43 |
|
|
|
′ |
|
−1 |
X |
|
|
|
|
= МУМНОЖ(B34 : Y37;B2 : E25) |
|||
|
|
X Ω |
|
|
|
|
|
|
|
|
|||||
I 40 : L43 |
|
′ |
−1 |
X ) |
−1 |
|
′ |
|
|
= МОБР(B40 : E43) |
|||||
|
(X Ω |
|
|
|
|
|
X Y |
|
|
||||||
O40 : O43 |
|
|
|
′ |
|
−1 |
|
|
|
|
|
= МУМНОЖ(B34 : Y37;A2 : A25) |
|||
|
|
X Ω Y |
|
|
|
|
|
||||||||
|
ˆ |
′ |
|
−1 |
X ) |
−1 |
X |
′ |
−1 |
|
|||||
R40 : R43 |
A = (X Ω |
|
|
|
|
Ω Y |
= МУМНОЖ(I40 : L43;O40 : O43) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
69

Рис. 4.13 – Расчет параметров модели ОМНК
70

|
Рис. 4.14 – Расчет матрицы Ω−1 в ОМНК |
|
|
||
Модель, |
построенная |
ОМНК, |
будет |
иметь |
вид |
yˆ′′= −3,55 + 0,33x1 + 4,82x4 −158,61x5 |
с коэффициентом |
детерминации |
|||
R2 = 97,7 % и |
средней относительной |
ошибкой |
аппроксимации |
||
Eср.отн. = 3,56 % . |
|
|
|
|
|
Так как в массиве данных наблюдалась незначительная гетероскедастичность, то качество моделей различаются незначительно (1– 2 %). Для прогноза и экономического анализа можно использовать вторую или третью модель. Выберем, например, вторую модель. Рассчитаем ее параметры матричным способом и используем для прогноза и анализа.
Таблица 4.6
Сравнение эконометрических моделей производительности труда
Модель |
Метод n |
R2 |
R2 |
Eср.отн. |
|
|
|
норм. |
|
yˆ |
3 |
= − 4,13 + 0,32x |
+ 4,99x |
4 |
−156,89x |
МНК |
24 |
97,75 % |
97,41 % |
3,78 % |
|
|
1 |
|
|
5 |
|
|
|
|
|
||
yˆ |
′ = − 4,61 + 0,31x |
+ 5,12x |
|
|
−154,09x |
МНК |
22 |
96,31 % |
95,69 % |
3 % |
|
|
|
1 |
|
4 |
5 |
|
|
|
|
|
|
yˆ |
′′= − 3,55 + 0,33x |
+ 4,82x |
4 |
−158,61x |
ОМНК |
24 |
97,73 % |
97,38 % |
3,56 % |
||
|
|
1 |
|
|
5 |
|
|
|
|
|
|
4.4 Экономический анализ и прогноз по многофакторной модели линейной регрессии. (задание 4.4 лабораторной работы 4)
4.4.1 Теоретические замечания
71

Прогнозное значение y pr определяется путем подстановки в
эмпирическое уравнение регрессии |
ˆ |
= aˆ0 + aˆ1 X1 + aˆ2 X 2 +... + aˆm X m |
Y |
соответствующих (известных) значений факторов-аргументов X j , j =1,m . Для этого формируется вектор X ′рr = (1, x1рr , x2 рr ,..., xm рr ). Тогда
|
|
|
|
|
|
|
|
yˆ рr = aˆ0 + aˆ1 x1 рr + aˆ2 х2 рr +... + aˆm хm рr . |
|
(4.33) |
|||||||||||||||||||||
Запишем соотношение (4.18) в матричном виде |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
yˆ рr |
= X ′рr |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.34) |
||||
|
|
|
|
|
|
|
|
A . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Доверительный интервал (с надежностью |
(1−α)) |
для |
значения |
||||||||||||||||||||||||||||
прогноза yрr |
имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
yˆ рr |
− ∆yрr ≤ yрr ≤ yˆ рr + ∆yрr , |
|
|
|
|
|
|
|
|
|
|
|
|
(4.35) |
|||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆y |
рr |
= S t |
1+ |
X ′ |
|
(X ′ X )−1 X |
рr |
. |
|
|
|
|
|
|
|
|
(4.36) |
||||||||||
|
|
|
|
|
|
|
|
|
e α |
|
|
рr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В (4.36) Se |
– среднеквадратическое отклонение ошибки модели, tα – |
||||||||||||||||||||||||||||||
табличный |
критерий |
|
|
Стьюдента |
при |
уровне |
|
значимости |
α , |
||||||||||||||||||||||
X ′рr = (1, x1рr , x2 рr ,..., xm рr ), (X ′ X )−1 – обратная матрица, полученная при |
|||||||||||||||||||||||||||||||
построении исходной модели множественной регрессии |
|
|
|
|
|
|
|
||||||||||||||||||||||||
yрr |
ˆ |
− |
Setα |
1 |
+ |
X |
′ |
|
′ |
|
−1 |
|
|
ˆ |
+ |
Setα |
1 |
+ |
|
′ |
|
|
′ |
|
−1 |
|
|
|
(4.37) |
||
yрr |
|
|
|
рr |
|
(XX ) |
|
Xрr ; yрr |
|
|
Xрr |
|
(XX ) |
|
|
Xрr . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение |
|
|
|
|
степени |
|
влияния |
|
фактор-аргументов |
на |
|||||||||||||||||||||
результирующий |
показатель |
|
Y . |
Важную |
роль |
при |
|
оценке |
влияния |
||||||||||||||||||||||
факторов играют коэффициенты построенной регрессионной модели. Коэффициент aˆ j показывает, что при увеличении xj на единицу его
измерения, зависимая переменная увеличится на aj единиц своего
измерения.
Однако непосредственно с их помощью нельзя сопоставлять факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и степени их колеблемости. Для устранения таких различий при экономической интерпретации степени влияния фактораргументов на результирующую функцию применяются коэффициенты эластичности Эj ; бета-коэффициенты βj ; дельта-коэффициенты ∆j .
Эластичность Y по отношению к X j определяется как процентное
72
изменение Y , отнесенное к соответствующему процентному изменению X j . Эластичность определяется соотношением
Эj = aˆ j |
x j |
|
|
|
|
|
|
, |
j =1,m . |
(4.38) |
|||||
y |
|||||||
|
|
|
|
|
|
||
Бета-коэффициент показывает, на какую часть величины среднеквадратического отклонения S y изменится зависимая переменная
Y , если соответствующая независимая переменная X j изменится на
величину своего среднеквадратического отклонения при фиксированном значении остальных независимых переменных.
Бета-коэффициент определяется по формуле
|
|
β j = aˆ j |
Sx |
|
|
|
|
|
|
|
|
|
|||
|
|
j |
, |
j =1,m , |
(4.39) |
||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
Sy |
|
|
|
|
|
|
|
||||
где |
|
|
n |
|
|
|
|
|
|
|
|
|
n |
||
|
1 |
|
|
|
|
|
|
|
|
1 |
|||||
Sx2j = |
|
∑(xi − |
x |
)2 |
, Sy2 = |
∑(y − |
y |
)2 . |
|||||||
|
|
|
|
||||||||||||
|
n −1 i=1 |
|
|
|
|
|
|
|
n −1 i=1 |
||||||
Долю влияния каждого фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэффициента
∆ |
j |
= r |
β |
j |
/ R2 . |
(4.40) |
|
|
|
yx j |
|
|
|
||
Здесь ryx j – коэффициент парной корреляции между |
j -м фактором и |
||||||
зависимой переменной, βj |
– |
бета-коэффициент, а R2 |
– коэффициент |
||||
детерминации регрессионной модели.
Таким образом, анализ влияния фактор-аргументов на результирующий признак Y позволяет проранжировать все фактораргументы по величине их влияния. Это дает возможность принимать меры воздействия при принятии решений по управлению результирующим признаком целенаправленно.
4.4.2 Организация данных и расчетов на листе MS Excel
Полученную во второй части лабораторной работы 3 модель используем для получения прогноза производительности труда при известных прогнозных значениях факторов-аргументов (рис. 4.15, 4.16).
73
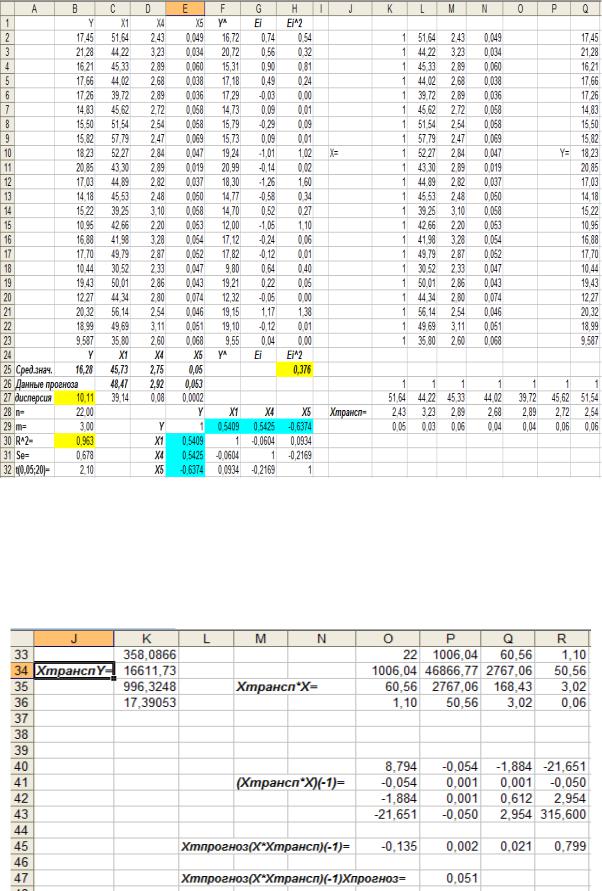
Рис. 4.15 – Организация данных и вспомогательные расчеты для прогноза
Для оценки влияния объясняющих переменных на результативный фактор вычислим коэффициенты эластичности, бета-коэффициенты и дельта-коэффициенты (ячейки B36 : B44 , рис. 4.17).
Рис. 4.16 – Расчет точечного и интервального прогноза. Продолжение 1
74

Рис. 4.17 – Расчет оценок влияния объясняющих переменных прогноза. Продолжение 2
Расчеты, приведенные на рис. 4.15 – 4.17, осуществлялись по формулам, описанным в табл. 4.7, 4.8 в последовательности их указания в таблице.
Таблица 4.7
Реализация в MS Excel лабораторной работы 4 (задание 4.4)
Адрес |
|
|
Формула |
|
Реализация в MS Excel |
|
ячейки |
|
|
|
|
|
|
1 |
|
|
|
2 |
|
3 |
B25: E25 , |
|
|
|
1 n |
|
B25 = СРЗНАЧ(B2 : |
H 25 |
|
|
x = n i∑=1xi |
B23) |
||
C26 : E26 |
|
|
1,06 x |
|
C26=C25*1,06 |
|
|
|
|
|
|
|
|
B28 |
|
Dy = 1 |
n |
|
= ДИСПР(B2 : B23) |
|
|
|
∑( yi − y)2 |
||||
|
|
|
n i =1 |
|
|
|
B30 |
R2 =1 |
− (1 |
n |
|
n |
=1 – H25/B27 |
|
∑ei 2 ) / 1 |
∑( yi − y)2 |
||||
|
|
n i =1 |
n i=1 |
|
||
B31 |
|
|
|
n |
2 |
= КОРЕНЬ(B28*H25/ |
|
|
|
|
∑e |
||
|
|
|
|
i |
|
|
|
|
Se |
= |
i =1 |
|
(B28 – B29 –1)) |
|
|
|
|
n − m −1 |
|
|
B33 |
tтабл. (α = 0,05;n − m −1) |
= СТЬЮДРАСПОБР |
||||
|
(0,05; B28 –B29 – 1) |
|||||
|
|
|
|
|
|
|
75

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение таблицы 4.7 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
O33: R36 |
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
= МУМНОЖ(K26 : |
|
||
|
|
|
|
|
|
|
|
|
X X |
|
|
|
|
|
|
|
|
|
|
AF29; K2 : N23) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
K33: K36 |
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
= МУМНОЖ(K26 : |
|
||
|
|
|
|
|
|
|
|
|
X Y |
|
|
|
|
|
|
|
|
|
|
AF29; Q2 : Q23) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
O40 : R43 |
|
|
|
|
|
|
|
′ |
−1 |
|
|
|
|
|
|
|
|
= МОБР(O33 : R36) |
|
|||
|
|
|
|
|
|
|
(X X ) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
E35 : E38 |
|
|
|
ˆ |
|
|
|
′ |
−1 |
|
′ |
|
|
|
|
|
|
= МУМНОЖ(O40 : |
|
|||
|
|
|
A = (X X ) X Y |
|
|
|
|
|
|
R43; K33 : K36) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ˆ |
|
|
|
|
ˆ |
|
|
|
|
|
|
|
= МУМНОЖ(E46 : |
|
||
|
E49 |
|
|
|
Ynp. =X ′np.A |
|
|
|
|
|
|
|
H46; E35 : E38) |
|
|||||||||
|
|
|
|
|
|
|
|
|
′ |
′ |
|
|
−1 |
|
|
|
|
|
|
= МУМНОЖ(E46 : |
|
||
|
O45 : R45 |
|
|
|
X np. (X X ) |
|
|
|
|
|
|
|
|
H46; O40 : R43) |
|
||||||||
|
|
|
|
|
|
′ |
|
|
|
′ |
−1 |
X np. |
|
|
|
|
|
|
= МУМНОЖ(O45 : |
|
|||
|
P47 |
|
|
X np. (X X ) |
|
|
|
|
|
|
|
|
R45; B48 : B51) |
|
|||||||||
|
H 49 |
ˆ |
|
|
|
|
|
|
|
′ |
|
|
′ |
|
|
−1 |
|
= B31*B32* |
|
||||
|
∆Ynp. |
|
|
|
|
|
|
|
|
|
|
|
|
X np. |
КОРЕНЬ(1+P47) |
|
|||||||
|
= Se tтабл. 1 + X np. |
(X X ) |
|
|
|
||||||||||||||||||
|
H 51 |
|
ˆ |
|
|
|
|
|
|
′ |
|
|
′ |
|
−1 |
X np. |
= B31*B32* |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КОРЕНЬ(P47) |
|
||||||||
|
∆MYnp. = Se tтабл. X np.(X X ) |
|
|
|
|||||||||||||||||||
|
D40 |
|
|
|
|
|
ˆ |
|
|
ˆ |
|
|
|
|
|
|
|
|
= E49 – H49 |
|
|||
|
|
|
|
|
Ynp. |
− ∆Ynp. |
|
|
|
|
|
|
|
|
|||||||||
|
G40 |
|
|
|
|
|
ˆ |
|
|
ˆ |
|
|
|
|
|
|
|
|
= E49 + H49 |
|
|||
|
|
|
|
|
Ynp. |
+ ∆Ynp. |
|
|
|
|
|
|
|
|
|||||||||
|
L60 |
|
|
|
|
|
ˆ |
|
|
|
ˆ |
|
|
|
|
|
|
|
= E49 – H51 |
|
|||
|
|
|
|
MYnp. |
− ∆MYnp. |
|
|
|
|
|
|
|
|||||||||||
|
O60 |
|
|
|
|
|
ˆ |
|
|
|
ˆ |
|
|
|
|
|
|
|
= E49 + H51 |
|
|||
|
|
|
|
MYnp. |
+ ∆MYnp. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.8 |
||
|
Реализация в MS Excel формул задании 3 (лаб. раб. 4) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Адрес |
|
|
|
Формула |
|
|
|
|
|
|
Реализация в MS Excel |
|||||||||||
|
ячейки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B34 : B36 |
|
Эj = aˆ j x j |
/ y j |
|
|
|
|
|
|
|
B34 = E36*C25/$B$25 |
|
|
|||||||||
|
B37 : B39 |
|
β j |
= aˆ j Sx j |
/ S y |
|
|
|
B37 = E36*КОРЕНЬ(C27/$B$27) |
|
|
||||||||||||
|
B40 : B42 |
|
∆ |
j |
= r |
β |
j |
/ R2 |
|
|
|
|
|
|
B39 = F32*B39/$B$32 |
|
|
||||||
|
|
|
yx j |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
B43 |
|
|
|
∑∆j |
|
|
|
|
|
|
|
|
|
B43 = СУММ(B40:B42) |
|
|
||||||
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
76
4.4.3 Выводы по результатам экономического анализа и прогноз по многофакторной модели линейной регрессии
В результате |
получим прогнозное значение производительности |
ˆ |
млн грн/г. при условии, что средние показатели по |
труда Ynp. =16,487 |
факторным признакам будут превышены на 6 %. Доверительные интервалы (с надежностью 95 %) для индивидуально прогнозного значения и математического ожидания прогноза соответственно будут иметь вид (15,026 ;17,947) и (16,165 ;16,808) .
Коэффициент эластичности Э1 показывает, что при увеличении
фондоемкости на 1 % производительность труда увеличивается на 0,89 %, при увеличении средней заработной платы на 1 % производительность труда увеличивается на 0,86 %, а при увеличении потерь рабочего времени на 1 % производительность труда уменьшается на 0,47 %.
Коэффициент β1 показывает, что при увеличении среднеквадратического отклонения Sx1 фондоемкости на 1 ед.
среднеквадратическое отклонение производительности труда увеличится на 0,62 %. Аналогично, при увеличении среднеквадратического отклонения средней заработной платы на 1 ед. среднеквадратическое отклонение производительности труда увеличится на 0,45 %. При увеличении среднеквадратического отклонения потерь рабочего времени на 1 ед. среднеквадратическое отклонение производительности труда уменьшится на
0,59 %.
Дельта-коэффициенты показывают, что 35 % производительности труда зависит от фондоемкости, 25 % – от средней заработной платы и 40 % – от потерь рабочего времени.
Для управления процессом, который исследуется (производительность труда) можно сделать вывод, что все три фактора оказывают примерно одинаковое влияние на производительность труда.
Для того, чтобы сделать окончательный вывод о возможности использования модели в экономическом анализе необходимо проверить для построенной модели выполнение условий Гаусса–Маркова (наличие гетероскедастичности и автокорреляции возмущений). Проверка этих условий будет рассмотрена в следующих лабораторных работах.
Задание 4.4 и лабораторная работа 4 выполнена полностью.
4.5 Вопросы для самопроверки к разделу 4
1.Модель множественной регрессии. Виды моделей множественной регрессии.
2.Теоретическое и эмпирическое линейное уравнение множественной регрессии.
3.Матричная форма записи и матричная формула оценки параметров множественной регрессии.
77
4.Две схемы отбора факторов для построения модели множественной регрессии.
5.Коэффициент множественной детерминации, коэффициент множественной корреляции. Скорректированный коэффициент множественной детерминации.
6.Проверка значимости множественного уравнения регрессии с помощью F-критерия Фишера.
7.Анализ статистической значимости параметров aˆ j модели.
8.Проверка выполнения предпосылок МНК.
9.Понятие мультиколлинеарности. Главные признаки мультиколлинеарности, последствия мультиколлинеарности. Методы ее устранения.
10.Способы обнаружения мультиколлинеарности. Обнаружение мультиколлинеарности с помощью алгоритма Феррара–Глобера: критерий
Пирсона χ2 , критерий Фишера Fk , tk j -критерий Стьюдента. Понятие
гомо– и гетероскедастичности. Примеры из экономики. Методы обнаружения гетероскедастичности, последствия гетероскедастичности.
11.Критерий µ обнаружения гетероскедастичности.
12.Тест Гольдфельда–Квандта для обнаружения гетероскедастичности.
13.Обобщенный МНК и его отличие от классического МНК (метод Эйткена).
14.Алгоритм построения и анализа регрессионных моделей.
15.Анализ влияния факторов на основе многофакторных регрессионных моделей: коэффициент эластичности; бета-коэффициент
βj и дельта-коэффициент ∆j .
16.Прогнозирование показателя Y по множественной регрессионной модели. Доверительный интервал для точечного прогноза.
78
