
- •Ю. Н. Полшков
- •СОДЕРЖАНИЕ
- •План
- •План
- •План
- •Рис. 3. Эллипс и его свойства
- •Рис. 4. Гипербола и ее свойства
- •Рис. 5. Парабола и ее свойства
- •Табл. 1. Данные примера 2
- •Молоко
- •Мы уже вводили понятие единичной матрицы
- •Рис. 3. Иллюстрация к теореме Ролля
- •Рис. 4. Иллюстрация к теореме Лагранжа
- •Рис. 4.18. График функции

6
ЧАСТЬ I АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Лекция 1. ПРОСТЕЙШИЕ ЗАДАЧИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
План
1.Система прямоугольных координат на плоскости и в пространстве. Числовая ось. Координаты точки.
2.Расстояние между двумя точками. Деление отрезка в заданном отношении.
3.Преобразование координат.
1. Аналитическая геометрия – это раздел математики, в котором свойства геометрических объектов (точек, линий, поверхностей, фигур, тел и т.п.) изучаются с помощью алгебры на основе метода координат.
Основоположником аналитической геометрии является Рене Декарт (1596-1650) – французский философ, математик, физик, физиолог. Он впервые в 1637 г. в своей книге “Геометрия” дал четкое изложение метода координат на плоскости. Декарт предложил положение точки на плоскости относительно заданной системы координат определять с помощью двух чисел – ее координат, а каждую линию на плоскости рассматривать как множество точек, заданных соответствующим геометрическим условием. Это условие записывается в виде уравнения, которое связывает переменные координаты точки, принадлежащей данной линии, и называется уравнением этой линии. Такой способ исследования геометрических объектов и называют методом координат.
Следующий важнейший вклад в аналитическую геометрию сделал французский математик и механик Жозеф Луи Лагранж (1736-1813), который впервые в 1788 г. в своей работе “Аналитическая механика” предложил определять положение вектора с помощью чисел – его проекций на координатные оси. Развитие идей Лагранжа привело к созданию векторной алгебры. Метод координат и аппарат векторной алгебры широко используется в современной аналитической геометрии.
Рассмотрим |
в |
пространстве точку |
O |
и три вектора i, j,k , где |
i |
= |
j |
= |
k |
=1, |
(i, j) = ( j,k) = (i,k) = |
π . |
Система векторов |
i, j,k |
называется ортонормированным базисом |
||||||
|
2 |
|
|
|
|
|
|
|
|
|
(“орто” означает взаимную перпендикулярность, “нормированность” – одинаковую единичную длину, понятие “базис” будет точно определено в разделе “Линейная алгебра”).
Рис. 1. Прямоугольная декартова система координат
Совокупность точки и базиса называется прямоугольной декартовой системой координат в пространстве и обозначается через Oxyz . Точка O называется началом

7
координат, а оси, которые проходят через начало координат в направлении базисных векторов, называются осями координат ( Ox – ось абсцисс, Oy – ось ординат, Oz – ось
аппликат). Плоскости, проходящие через оси координат, называют координатными плоскостями и обозначают Oxy,Oyz,Ozx . При изображении системы координат, как
правило, указывают оси и не указывают векторы i, j, k .
Пусть задана прямоугольная система координат Oxyz и произвольная точка M (рис.
1). Радиус-вектор r = OM этой точки записывают в виде |
|
r = xi + y j + zk или r = (x; y; z) . |
(1) |
Координаты x, y, z этого радиус-вектора называются координатами точки M . Точка M с координатами x, y, z обозначается через M (x; y; z) .
Из ортогональности базисных векторов системы Oxyz следует, что координаты точки M равны соответствующим проекциям радиус-вектора этой точки на оси координат, т.е.
x = npOx OM , y = npOy OM , z = npOz OM , |
(2) |
и определяются проектированием точки M на координатные оси (рис. 1).
Прямоугольные координаты точки на плоскости и на прямой определяются таким же образом, как и в пространстве. Прямоугольная система координат Oxy на плоскости задается
точкой O – началом координат и двумя взаимно перпендикулярными единичными векторами i, j – базисом системы координат; система координат на прямой задается точкой O и единичным вектором i . Понятно, что точка M (x; y) на плоскости имеет лишь две координаты (абсциссу и ординату), а точка M (x) на прямой – одну.
2. Пусть начало вектора a = AB находится в точке A(x1; y1; z1 ) , а конец – в точке B(x2 ; y2 ; z2 ) . Координаты этого вектора определяются как ax = x2 − x1 , ay = y2 − y1 , az = z2 − z1 , т.е.
|
|
|
AB = (x2 − x1; y2 − y1; z2 − z1 ) . |
(3) |
|||||
Тогда длина вектора AB : |
|
|
|
|
|
|
|||
|
AB |
|
= (x2 − x1 )2 +( y2 − y1 )2 +(z2 − z1 )2 . |
(4) |
|||||
|
|
||||||||
Этой формулой пользуются для нахождения расстояния между точками A и B . |
|
||||||||
Например, нужно найти расстояние |
|
между точками A(0;−1;2) и B(−1;1;4) . |
В |
||||||
соответствие с (3) и (4) имеем: AB = (−1;2;2) ; |
|
AB |
|
= |
1+4 +4 = 3. |
|
|||
|
|
|
|||||||
Пусть теперь необходимо найти на отрезке |
AB такую точку M (x; y; z) , которая бы |
||||||||
делила этот отрезок в отношении λ , т.е. AM : MB = λ . Формула координат точки деления отрезка в заданном отношении λ имеет вид:
x = |
x1 +λx2 |
, |
|
y = |
y1 +λy2 |
|
, |
z = |
z1 +λz2 |
. |
(5) |
|||||
|
|
|
|
1+λ |
|
|
||||||||||
|
1+λ |
|
|
|
|
|
|
1+λ |
|
|||||||
В частности, при делении отрезка пополам ( λ =1 ), получаем |
|
|||||||||||||||
x = |
x1 + x2 |
, |
y = |
y1 + y2 |
, |
|
z = |
z1 + z2 |
. |
(6) |
||||||
|
|
|
|
|||||||||||||
2 |
|
|
2 |
|
|
|
2 |
|
|
|
||||||
3. При решении задач иногда нужно переходить от одной прямоугольной системы координат к другой. Выполняется такой переход с помощью формул преобразования координат.
Рассмотрим преобразование координат на плоскости. Возьмем две прямоугольные декартовы системы координат Oxy и O1 XY с разными началами координат и одинаково
направленными осями. Пусть точки O1 и M в системе Oxy имеют, соответственно,
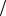
|
8 |
координаты (a;b) и (x; y) . Тогда координаты точки M |
в системе O1 XY удовлетворяют |
равенствам |
|
X = x −a , Y = y −b . |
(7) |
Формулы (7) называются формулами преобразования координат при параллельном переносе осей. Они выражают координаты точек в системе O1 XY через координаты точек в системе
Oxy .
Пусть на плоскости заданы две прямоугольные системы координат Oxy и OXY , имеющие общее начало O , причем система OXY получена из системы Oxy поворотом осей
на положительный угол α . Тогда формулы преобразования координат при повороте осей
имеют вид
X = x cosα + y sinα , Y = −xsinα + y cosα . |
(8) |
|||
Например, в системе координат Oxy точка M |
имеет координаты (2;4) . Найдем ее |
|||
координаты в системе OXY , которая получена из системы Oxy |
поворотом на угол π 2 . |
|||
Согласно (8), получим |
|
|
|
|
X = 2cos π |
+ 4sin π = 4 , |
Y = −2sin |
π α + 4cos |
π = −2 . |
2 |
2 |
|
2 |
2 |
Заметим, что аналогичный результат можно получить геометрически, построив точку M и системы координат Oxy , OXY .
