Рис. 4.18. График функции y = e−x2 / 2

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный университет

Предмет:

Высшая математика

Файл:

Полшков Ю.Н. Курс лекций по высшей математике.pdf

Скачиваний:

206

Добавлен:

13.04.2015

Размер:

4.9 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1111

					90
	1	2		′′
Например, функция y =	2 x		+cos x имеет вторую производную y	′′	=1−cos x , которая
Например, функция y =	2 x		+cos x имеет вторую производную y		=1−cos x , которая
равна нулю при x = 2πk, k Z	. Однако критические точки второго рода				x = 2πk, k Z не

являются абсциссами точки перегиба. В тоже время, функция y = x3 имеет критическую

точку второго рода x = 0 , которая является абсциссой точки перегиба.

Следующая теорема определяет достаточные условия существования точки перегиба. ТеоремаU 2 (достаточные условия точки перегиба).U Пусть x0 –

критическая точка второго рода функции f (x) . Если при переходе через точку

	′′
x0 вторая производная f (x) меняет знак на противоположный, то точка
(x0 ; f (x0 )) является точкой перегиба кривой y = f (x) .
ПримерU	1.U Найти интервалы выпуклости и точки перегиба функции y = e−x2 / 2 .

Решение. Область определения функции D( y) = R . Находим вторую производную y′′ = (−xe−x2 / 2 )′ = −e−x2 / 2 + x2e−x2 / 2 = (x2 −1)e−x2 / 2 .

Решив уравнение y′′ = 0 , получим критические точки второго рода x1 = −1 и x2 =1. Других критических точек нет, так как y′′ = (x2 −1)e−x2 / 2 существует во всех точках D( y) = R .

Эти точки разбивают R на три промежутка (−∞,−1), (−1,1) и (1,+∞). На каждом из промежутков рассчитаем знак второй производной: если x (−∞,−1), то y′′(x) > 0 – график функции выпуклый вниз; если x (−1,1), то y′′(x) < 0 – график функции выпуклый вверх; если x (1,+∞), то y′′(x) > 0 – график функции выпуклый вниз (теорема 1). При переходе через критические точки второго рода x1 = −1 и x2 =1 вторая производная меняет свой знак на противоположный. Согласно теореме 2, точки (−1;e−1/ 2 ) и (1;e−1/ 2 ) будут точками перегиба (рис. 4).

= 2 −0 = 2 .

2. Важным понятием математического анализа являются асимптоты кривой.

ОпределениеU 4.U Прямая l называется асимптотой кривой, если расстояние δ от переменной точки M кривой до этой прямой стремится к нулю, когда точка M , двигаясь по кривой, удаляется в бесконечность.

Асимптоты принято делить на вертикальные, горизонтальные и наклонные [похилі]. Они изображены на рис. 5 а), б) и в), соответственно.

k = lim

x→∞

а)	б)	в)
	Рис. 5.18. Асимптоты кривых
Для существования вертикальной асимптоты x = x0		у функции y = f (x) необходимо
и достаточно, чтобы	f (x) = ∞ , или lim f (x) = ∞ , или lim f (x) = ∞ .
lim	f (x) = ∞ , или lim f (x) = ∞ , или lim f (x) = ∞ .
x→x0 −0	x→x0 +0	x→x0

Вертикальные асимптоты следует искать в точках разрыва второго рода. Например,

гипербола y = 1x имеет единственную точку разрыва второго рода x0 = 0 . Так как

lim	1		1	= ∞,
lim	x	=		= ∞,
x→0	x		0

то x = 0 – вертикальная асимптота. Для функции y = ctgx вертикальными асимптотами будут прямые x =πk, k Z .

Для существования наклонной асимптоты у функции y = f (x) необходимо и

достаточно, чтобы существовал конечный предел

f (x) . x

Тогда наклонная асимптота записывается следующим образом: y = kx +b ,

где b определяется как конечный предел

b = lim( f (x) −kx).

x→∞

Горизонтальная асимптота является частным случаем наклонной при k = 0 и записывается в виде

y = b .

Поэтому часто различают не три, а два типа асимптот: вертикальные и невертикальные.

Например, функция

y =

имеет

наклонную

асимптоту y = x (рис.

6).

Действительно,

k = lim

x3 + 4

= lim 1+

=1,

x→∞

x3 + 4

− x3

b = lim

−1 x

= lim

= 0 .

x→∞

x→∞ x

Графики функций могут иметь асимптоты разных типов. Например, гипербола y =

кроме вертикальной асимптоты x = 0 имеет и горизонтальную

y = 0 . В этом случае график

функции нигде не пересекает своих асимптот (рис. 6). Отметим, что графики функций могут пересекать свои горизонтальные и наклонные асимптоты. Например, график функции

								92
y =		x3	пересекает свою наклонную асимптоту		y = −x в точке (0;0),		а график функции
y =	1	− x2	пересекает свою наклонную асимптоту		y = −x в точке (0;0),		а график функции
	1	− x2
y =		x −2		пересекает свою горизонтальную асимптоту y = −1 в точке		3
							;−1	(рис. 7).
		x2 +	1				;−1	(рис. 7).
		x2 +	1			4

Рис. 6. Графики функций y =	1	(слева) и	y =	x3 +4	(справа)
	x			x2

Рис. 7. Графики функций y =		x3	(слева) и	y =	x −2			(справа)
		1− x2			x2	+	1

ЗамечаниеU	1.U Асимптоты кривой	y = f (x) при		x → −∞		и x → +∞ могут быть

разными. Поэтому при нахождении асимптот нужно вычислять пределы как при x → −∞ , так и при x → +∞.

Например, график функции	y =	x −2		имеет две асимптоты y = −1 и y =1 (рис. 7),
		x2 +1
т.к.
	x −2				x −2
lim			= −1,	lim			=1.
	x2 +	1			x2 +	1
x→−∞				x→+∞

Нахождение асимптот позволяет более четко представить поведение графика функции. Отметим, что не у всякой кривой, уходящей в бесконечность, есть асимптота.

Например, парабола y = x2 асимптот не имеет.

3. Одной из главных задач математического анализа является исследование поведения функции и построение ее графика. Изложим примерную схему этого процесса:

1)найти область определения функции;

2)найти (если это возможно) точки пересечения графика с координатными осями;

3)исследовать функцию на периодичность, четность и нечетность;

4)найти точки разрыва и исследовать их;

5)найти интервалы монотонности, точки локальных экстремумов и значение функции

вэтих точках;

6)найти интервалы выпуклости и точки перегиба;

7)найти асимптоты кривой;

8)поместить полученные данные во вспомогательную таблицу;

9)построить график функции.

Если изучаемая функция является периодической с периодом T , то достаточно построить ее график на отрезке [0,T ], после чего повторить этот график на промежутках

nT ,(n +1)T ,		n = ±1,±2,...

	Если функция четная (или нечетная), то достаточно построить ее график для x ≥ 0 , а
потом отобразить его симметрично относительно оси				Oy (или	относительно начала
координат).			2x −1
	ПримерU	2.U Исследовать функцию y =		методами	дифференциального
			(x −1)2

исчисления и построить ее график.

Решение. Будем придерживаться общей схемы исследования функций.

1)Функция не определена при x =1. Область определения функции: D( y) = R \ {1}

или D( y) = (−∞,1) (1,+∞).

2)Найдем точки пересечения с осью Oy , т.е. x приравняем к 0 и найдем значения

функции. При x = 0 имеем f (0) = −1.	Точкa	пересечения с осью	Oy имеет координаты
(0;−1). Найдем точки пересечения с	осью	Ox , т.е. вычислим	действительные корни


уравнения			f (x) = 0 :
				2x −1	= 0 x		= 1 .
					= 0 x		= 1 .
				(x −1)2			2
	1	;0
Точка	2	;0	– точка пересечения с осью Ox .
	2
3) Функция непериодическая. Проверим функцию на четность (нечетность). Для этого
вместо x подставим в функцию (−x) :
			f (−x) = 2(−x) −1			= −	2x +1	.
			f (−x) = 2(−x) −1			= −		.
				(−x −1)2			(x +1)2
Так как	f (−x) ≠ f (x) , то функция не является четной. Так как f (−x) ≠ − f (x) , то функция не

является нечетной.

4) В точке x =1 функция терпит разрыв. Вычислим в этой точке левосторонний и правосторонний пределы:

	2x −1		1			2x −1
lim		=		= +∞ ,	lim
lim	(x −1)2	=		= +∞ ,	lim	(x −1)2
x→1−0	(x −1)2		+0		x→1+0	(x −1)2

Следовательно x =1 – точка разрыва второго рода.

5) Вычислим первую производную нашей функции:

=+1 = +∞ .0

′

(2x −1)′(x −1)2 −((x

−1)2 )′(2x −1)

2(x −1)2

−2(x −1)(2x −1)

−2x

(x) =

(x −1)4

(x −1)3

Согласно

необходимому условию

экстремума,

приравняем первую производную к 0 и

найдем стационарные точки:

−2x

= 0 x = 0 .

(x −1)3

Первая производная не существует в точке x =1, но она не входит в область определения

функции. Следовательно, критической точкой функции является только x = 0 . Воспользовавшись достаточным условием возрастания и убывания функции, найдем

интервалы монотонности функции. Наша функция возрастает при		′
интервалы монотонности функции. Наша функция возрастает при		x [0,1), так как f (x) ≥ 0 .
И убывает при x (−∞,0]	(1,+∞), так как f (x) ≤ 0 .
	′
Найдем координаты точек экстремума функции. Согласно достаточному условию
экстремума в точке x = 0	функция имеет локальный минимум ymin = f (0)= −1 . Локальных

максимумов функция не имеет.

6) Вычислим вторую производную нашей функции:

′′

−2x

′

(

)

(

)

(

)

(

)

−2

x −1 3

+6x

x −1

−2

x −1

+6x

2x +1

f (x) =

(x −1)3

−1)6

(x −1)4

Для нахождения критических точек второго рода,

приравняем вторую производную к 0 и

решим это уравнение:

2(2x +1)

= 0

x = −1 .

(x −1)4

Вторая производная не существует в точке x =1,

но она не входит в область определения

функции. Следовательно, критической точкой второго рода будет только x = −

1 .

По

теореме

найдем промежутки

выпуклости

функции.

Решив неравенство

′′

получим,

что при

(1,+∞)

график функции выпуклый вниз. Далее

f (x) ≥ 0 ,

x −

решаем неравенство

′′

и получаем, что при

−∞,−

график функции выпуклый

(x) ≤ 0

вверх.

x = −1

При переходе через критическую точку второго рода

вторая производная

меняет свой знак на противоположный. Согласно достаточному условию точки перегиба,

−	1	;−	8	будет точкой перегиба.
	2		9

7) Из п. 4 следует, что прямая x =1 является вертикальной асимптотой исследуемой кривой. Определим, имеются ли у кривой невертикальные асимптоты. Для этого рассчитаем предел:

k = lim	f (x)	= lim	2x −1	= 0 .
	x
x→∞		x→∞ x(x −1)2

Следовательно наклонной асимптоты нет. Проверим наличие горизонтальной:

b = lim( f (x) −kx)= lim		2x −1	= 0 .
		(x −1)2
x→∞	x→∞

Значит прямая y = 0 является горизонтальной асимптотой нашей кривой.

8) Поместим полученные данные во вспомогательную табл. 1. В первую строку таблицы занесем критические точки и точки разрыва функции. Эти точки разбивают область определения функции на конкретное число интервалов, в каждом из которых мы рассчитываем знак первой и второй производной, выясняем характер монотонности и

выпуклости функции. Значки и обозначают, соответственно, возрастание и убывание функции на промежутке. Значки и ∩ обозначают выпуклость вниз и вверх, соответственно. Совместный значок описывает одновременно характер монотонности и

выпуклости функции. Например,

∩ означает, что

на промежутке

функция

убывает,

будучи выпуклой верх.

Табл. 1. Вспомогательные сведения для построения графика функции y

2x −1

(x −1)2

−∞,−

−

(0,1)

(1,+∞)

−

′

−

f (x)

′′

−

f (x)

∩

−

−1

min

nep

9) Построим график функции, нанеся на него асимптоты.

	Рис. 8. График функции y =	2x −1
	Рис. 8. График функции y =	(x −1)2
		(x −1)2

z = f (x, y) .

I I I.в ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ

Лекция 1. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ

План

1.Понятие функции многих переменных.

2.Предел и непрерывность функции многих переменных.

1. Ранее рассматривались числовые функции y = f (x) одной переменной						x .	Областью
определения такой функции являлось множество		X R . Числовая функция n переменных
характеризуется тем, что областью ее определения является подмножество X пространства
Rn ,	n >1. В этом случае значение аргумента x представляет собой точку (x , x ,..., x ) Rn .
					1	2	n
	Определение 1. Пусть имеются два множества X Rn		и Y R , и указано правило f ,
по	которому каждому элементу (x1 , x2 ,..., xn ) X	ставится	в	соответствие		единственный
элемент y Y . Тогда говорят, что задана функция n переменных				f из X	в Y :
	y = f (x1 , x2 ,..., xn ) .						(1)
Как и ранее, D( f ) = X – область определения функции f ,			E( f ) =Y		– область значений
функции f .
	Для функций двух переменных ( n = 2 ) вместо x1 , x2 , y		пишут обычно x, y, z , и тогда
(1) принимает вид

(2)

Функция двух переменных геометрически определяет некоторую поверхность в R3 . Ее область определения состоит из точек P(x, y) расположенных на плоскости xOy . Каждой

из этих точек соответствует единственная число z = f (x, y) , которое является аппликатой точки M (x, y, z) данной поверхности. Поэтому говорят, что z есть функция точки P(x, y) , и пишут z = f (P) . Эту аналогию можно распространить на случай n > 2 . Тогда область определения будет состоять из точек P(x1 , x2 ,..., xn ) , а функция (1.19) будет записана в виде y = f (P) .

Поверхность x2 + y2 + z2

= R2

– это сфера радиуса R с центром в точке (0,0,0) . Она

не является функцией двух переменных, так как точке

P(x, y)

соответствуют два числа

= ± R2 − x2

− y2

. Однако

функцией

будет, например,

верхняя

часть сферы

1,2

z =

R2 − x2 − y2 (рис. 1, а).

Другим

примером функции

двух

переменных

может

служить

эллиптический

параболоид z =

(рис. 1, б). Если эту поверхность пересечь плоскостью, параллельной

плоскости xOy , то линией пересечения будет эллипс. Если же плоскость пересечения параллельна xOz или yOz , то линией пересечения будет парабола.

Уравнением z =	x2	−	y2	задается гиперболический параболоид. График этой функции
	a2		b2

двух переменных имеет форму седла (рис. 1, в). Если эту поверхность пересечь плоскостью, параллельной плоскости xOy , то линией пересечения будет гипербола. Если же плоскость

пересечения параллельна xOz или yOz , то линией пересечения будет парабола.

Еще одним примером функции многих переменных может служить производственная функция Кобба-Дугласа. Ее классический вид

где z – объем		z = a0 xa1 y1−a1 ,				где y		(3)
	выпуска	продукции;	где x	–	затраты труда;		–	затраты
производственных фондов (рис. 2). Константы a0 и a1					– положительны, как и переменные x ,
y , z . Сумма параметров a1		и 1−a1 равна единице. Это означает,				что при увеличении
производственных	ресурсов	x и y	на одну	единицу объем продукции			z	также

увеличивается на единицу. Следовательно, темпы роста перечисленных показателей совпадают.

	Исследования показали, что зависимость (3) редко встречается на практике. Поэтому
справедлив более общий вид производственной функции Кобба-Дугласа:		(4)
	z = a0 xa1 ya2 ,
где a2	– положительная константа. В отличие от предыдущего случая сумма параметров
a1 +a2	может быть как больше, так и меньше единицы. Если a1 +a2 >1 , то темпы роста
объема выпуска продукции z выше, чем темпы роста производственных ресурсов		x и y .

Если же a1 +a2 <1, то, наоборот, темпы роста объема выпуска ниже темпов роста ресурсов.

а)

б)

в)

Рис. 1. Примеры графиков функций двух переменных

Рис. 2. График производственной функции Кобба-Дугласа
2. Рассмотрим две точки из	пространства Rn :	P(x , x ,..., x )		и	P (x 0	, x	0 ,..., x 0 ) . Как
		1 2	n		0 1	2	n
известно, расстояние между ними определяется формулой
ρ(P, P0 )=	(x1 − x10 )2 +(x2 − x2	0 )2 +... +(xn − xn		0 )2 .
Определение 2. Число	A называется пределом функции			f	в точке		P0 , если при

ρ(P, P0 )→ 0 разность f (P) − A будет бесконечно малой величиной. В этом случае пишут:

lim f (P) = A .

P→P0

Причем, способ приближения точки P к P0 может быть любым (например, по любой

линии).

Все свойства пределов, установленные ранее для функций одной переменной, остаются справедливыми для функций n переменных.

Определение	3.	Функция	f ,	определенная	на	множестве	X Rn ,	называется
непрерывной в точке P0 X , если
			lim f (P) = f (P0 ) .
			P→P0
Определение	4.	Функция	f ,	определенная	на	множестве	X Rn ,	называется

непрерывной на этом множестве, если она непрерывна в каждой точке множества X . Приведем ряд важных результатов, касающихся непрерывных функций многих

переменных.

Теорема 1. Любая элементарная функция непрерывна на всей области ее определения.

Определение 4. Пусть X – множество в пространстве Rn . Точка P называется: 1) внутренней точкой множества X , если существует шар B(P,r) радиуса r , все точки

которого принадлежат X ; 2) внешней точкой по отношению к X , если существует шар B(P,r) , ни одна точка которого не принадлежит X ; 3) граничной точкой для X , если она не

является ни внутренней, ни внешней точкой X , иначе говоря, если любой шар с центром P содержит как точки, принадлежащие X , так и точки, не принадлежащие X (рис. 3, а).

а)

б)

Рис. 3. Иллюстрация типов точек по отношении к множеству X

Из определения 4 следует, что любая точка пространства Rn является либо внутренней точкой для множества X , либо внешней, либо граничной по отношению к X . При этом любая внутренняя точка принадлежит множеству X , любая внешняя точка не принадлежит X ; что же касается граничных точек, то они могут как принадлежать, так и не принадлежать X .

На рис. 3, б) множество X представляет собой круг на плоскости (в R2 ) вместе с граничной окружностью; граничными точками множества X являются точки этой окружности. Если в качестве X взять круг без граничной окружности, множество граничных точек останется тем же.

Определение 5. Множество X называется открытым, если все его точки внутренние. Множество X называется замкнутым, если оно содержит все свои граничные точки.

Упомянутый выше круг X (рис. 3, б) без граничной окружности является открытым множеством; тот же самый круг вместе с граничной окружностью – замкнутое множество.

		99
Теорема 2. Если непрерывная числовая функция	f	от n переменных
задана на ограниченном и замкнутом множестве X Rn ,	то она ограничена на
этом множестве.	f	от n переменных
Теорема 3. Если непрерывная числовая функция	f	от n переменных
задана на ограниченном и замкнутом множестве X Rn ,	то существует точка
P0 X , в которой f принимает свое наименьшее значение,		и точка Q0 X , в
которой f принимает свое наибольшее значение на X .

100

Лекция 2. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ

План

1.Частные производные.

2.Полный дифференциал и дифференцируемость функции.

3.Эластичность функции многих переменных.

4.Частные производные высших порядков.

1. Ограничимся случаем функций двух переменных. Все дальнейшее справедливо, однако, и в том случае, когда число переменных равно трем, четырем и т.д.

Итак, пусть в некоторой окрестности точки (x0 , y0 ) определена функция z = f (x, y) . Определим приращения переменных x и y формулами:

∆x = x − x0 , ∆y = y − y0 .

Тогда любая точка (x, y) из окрестности точки (x0 , y0 ) может быть представлена как

(x, y) = (x0 +∆x, y0 +∆y) .

При изменении x от x0 до x0 +∆x (и постоянном y = y0 ) функция z изменяется на

величину

∆x z = f (x0 +∆x, y0 ) − f (x0 , y0 ) .

Эта разность называется частным приращением функции z по x . Частное приращение по y

определяется аналогично:

∆y z = f (x0 , y0 +∆y) − f (x0 , y0 ) .

Определение 1. Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения частного приращения функции к приращению соответствующей независимой переменной, когда это приращение стремиться

к нулю.

∂z

Частные производные по

x функции

z = f (x, y) обозначают, как

f / ,

по y –

∂z

∂x

как

, f / . Если частная производная

вычисляется

конкретной

точке,

то

пишут

∂y

z/ (x , y

) . Согласно определению 1, имеем

∆x z

f (x0 +∆x, y0 ) − f (x0 , y0 )

zx/ = lim

= lim

(1)

∆x→0

∆x

∆x→0

∆x

zy/ = lim

∆y z

= lim

f (x , y

+ ∆x) − f (x , y

)

(2)

∆y

∆y→0

Из определения следует, что для нахождения частной производной fx/ (x, y) можно

использовать правила дифференцирования функции одной переменной, считая переменную y константой.

Пример 1. Найти частные производные функций: а) z = xy ; б) z = xy .

Решение. а) Считая y = const , находим z/	=	1	. Считая x = const , находим z/	= −	x	.
		y
x			y		y2
б) Частная производная zx/ = yxy−1 вычисляется	как		производная степенной функции, а

частная производная zy/ = xy ln x вычисляется как производная показательной функции.

	101
2. Рассмотрим одновременное изменение независимых переменных x и	y . Тогда функция
z = f (x, y) изменится на величину
∆z = f (x0 +∆x, y0 +∆y) − f (x0 , y0 ) .	(3)

Величина ∆z , заданная формулой (3.20), называется полным приращением функции z в точке (x0 , y0 ) . Так же, как и случае функции одной переменной возникает задача о

приближенной замене приращения ∆z (которое как правило, является нелинейной функцией от ∆x и ∆y ) на линейную функцию от ∆x и ∆y . Роль линейного приближения выполняет

полный дифференциал функции, который определяется как сумма произведений частных производных функции на приращения независимых переменных. Так, в случае функции двух переменных, полный дифференциал определяется равенством

dz = zx/ ∆x + zy/ ∆y .

(4)

В формуле (4) точка (x0 , y0 ) явно не указана, однако, следует помнить, что в различных точках (x0 , y0 ) дифференциал будет различным.

Дифференциалами независимых переменных x и y	назовем их приращения
dx = ∆x и dy = ∆y . Поэтому (4) можно записать так:
dz = zx/ dx + zy/ dy .	(5)

Пример 2. Найти полный дифференциал функции z = xy и вычислить его в точках: а)

(0;2), б) (1;1).

Решение. Запишем полный дифференциал в общем виде dz = zx/ dx + zy/ dy = 1y dx − yx2 dy .

Подставив координаты точек, получим

dx −

dy =

1 dx ;

(0;2)

dx −

dy = dx −dy .

(1;1)

Определение 2. Функция z = f (x, y)

называется дифференцируемой в точке (x0 , y0 ) ,

если ее полное приращение можно представить в виде

(6)

∆z = f (x, y) − f (x0 , y0 ) = fx/ (x0 , y0 )∆x + fy/ (x0 , y0 )∆y +ερ ,

или, короче,

∆z = dz +ερ ,

где ρ = (∆x)2 +(∆y)2 – расстояние от точки (x, y) до точки (x0 , y0 ) ; ε =ε(∆x,∆y) – функция, бесконечно малая при ∆x → 0 , ∆y → 0 , т.е.

lim ε(∆x, ∆y) = 0 .

∆x→0 ∆y→0

Теорема 1. Если функция z = f (x, y) дифференцируема в точке (x0 , y0 ) , то

она непрерывна в этой точке.

Теорема 2 (достаточное условие дифференцируемости). Если частные производные f / x (x, y) и f / y (x, y) определены в окрестности точки (x0 , y0 ) и эти

производные непрерывны в самой точке (x0 , y0 ) , то функция z = f (x, y) дифференцируема в этой точке.

102

3. Ранее было введено понятие эластичности функции одной переменной. Аналогично вводится это понятие и для функции нескольких переменных.

Пусть, например,		z = f (x, y)			–		функция	двух переменных;
∆x z = f (x0 +∆x, y0 ) − f (x0 , y0 ) ,	∆y z = f (x0			, y0 +∆y) − f (x0 , y0 ) – ее частные приращения.
Определение 3. Эластичностью функции							z = f (x, y)	в точке (x0 , y0 ) по
переменной x называется предел					∆x z		∆x .
	E	zx	(x , y	) = lim	∆x z	:	∆x .
		zx	0 0
				∆x→0	z		x

Эластичностью z по y в той же точке:

∆y z

∆y

Ezy (x0 , y0 ) = lim

∆y→0 z

Говорят, что Ezx – коэффициент эластичности

z по

x ,

а Ezy – коэффициент

эластичности z

по y (обозначение точки часто опускается).

Из определения вытекают следующие формулы:

Ezx (x, y) =

zx/

= x(ln z)/x ,

Ezy (x, y) =

zy/

= y(ln z)/y .

(7)

Пример 3. Найти коэффициенты

эластичности по x и y

производственной функции Кобба-Дугласа z = a xa1 ya2

в точке (x , y ) .

Решение. Согласно формулам (7) имеем

(x, y)

= x(ln z)/ = x(ln[a xa1

ya2 ])/ = x(ln a

+ a ln x + a

ln y)/

= x

= a ,

Ezy (x, y) = y(ln z)/y

= a2 .

Следовательно, в любой точке (x0 , y0 ) коэффициенты производственной


функции Кобба-Дугласа постоянны и равны:			Ezx = a1 ,	Ezy = a2 .
4. Пусть	D R2 – открытое множество в		R2 ,	f (x, y) –	определенная на
множестве	D функция.	Предположим, что в каждой точке M D существуют
частные производные		fx/ и fy/ . Тогда частные производные			fx/ (x, y) и fy/ (x, y)
естественно считать функциями с областью определения D .					Они называются

частными производными первого порядка. Частные производные от функций

fx/ (x, y) и

fy/ (x, y)

называются

частными

производными второго

порядка

от

функции f (x, y) .

Частные производные

от частных

производных второго

порядка называются частными производными третьего порядка и т.д.

Если

первая производная

функции

z = f (x, y) была взята,

скажем,

по

переменной x , то ее частные производные в точке (x0 , y0 ) обозначаются так:

z//

= (z

/ )

= f //

(x , y ) ,

z//

= (z

= f // (x , y

) ,

или

∂2 f (x , y )

∂2 z

∂

∂z

∂

2 z

∂ ∂z

2 =

∂x

∂y∂x

∂y

∂x

∂y∂x

Аналогичные обозначения используются и для других частных производных.

Например, zyx// = (zy/ )/x , zyy// = (zy/ )/y , zxyx/// = ((zx/ )/y )/x и т.д.

Частные производные второго порядка zxy// и zyx// называются смешанными частными производными.

103

Пример 4. Найти все частные производные второго порядка от функций:

а)

z = x3 + y2 +5x2 y ; б)

z = arctg

Решение.

а)

Имеем

zx/

= 3x3

+10xy ,

zy/ = 2 y +5x2 .

Следовательно,

zxx//

= 6x +10 y ,

zyy//

= 2 ,

zxy//

= zyx//

=10x .

б)

Имеем

−x

. Следовательно,

z/ / = −

2xy

(x2 + y2 )2

x2 + y2

x x

z//

2xy

, z// = z

x2 − y2

(x2 + y2 )2

Обратим внимание на то, что в примере 4 смешанные частные производные от одной и той же функции z совпадают. Являются ли данные совпадения случайными, или они – следствия какого-то общего правила? Следующая теорема дает ответ на этот вопрос.

Теорема 3. Если производные fxy// (x, y) и fyx// (x, y) существуют в некоторой окрестности точки P(x0 , y0 ) и непрерывны в самой точке P , то они равны

между собой:

fxy// (P) = fyx// (P) .

104

Лекция 3. ЭКСТРЕМУМЫ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ. ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ

План

1.Локальный экстремум функции двух переменных и его необходимые условия.

2.Достаточные условия экстремума функции двух переменных.

3.Производная по направлению.

4.Градиент.

1. Рассмотрим	функцию		z = f (x, y) , которая определена и непрерывна в
некоторой окрестности точки M0 (x0 , y0 ) .
Определение	1.	Точка	M0	называется точкой локального максимума
(минимума) функции		z = f (x, y) ,		если существует такая окрестность точки M0 ,

вкоторой для любой точки M (x, y) из этой окрестности выполняется

неравенство f (M ) ≤ f (M0 ) ( f (M ) ≥ f (M0 ) ).

Точки локального максимума и локального минимума называются точками локального экстремума или просто точками экстремума.

Теорема 1 (необходимое условие экстремума). Если функция z = f (x, y) имеет частные производные первого порядка в точке локального экстремума

M0 (x0 , y0 ) , то

		fx/ (M0 ) = fy/ (M0 ) = 0 .
Доказательство.		Рассмотрим	сначала	функцию	одной	переменной
f (x, y ) .	Производная этой функции совпадает с частной производной f / (x, y ) ,
0						x	0
а сама	функция имеет	локальный	экстремум	в точке	x0 . По	теореме	3.17

(необходимое условие локального экстремума функции одной переменной)

производная

функция

f (x, y )

в точке

равна

нулю,

т.е.

f / (x, y

) = 0 .

Аналогично функция одной переменной

f (x, y0 )

имеет локальный экстремум в

точке

y = y0 .

Следовательно,

ее

производная

этой

точке

равна

нулю, т.е.

f / (x, y ) = 0 . Теорема доказана.

Итак, «подозрительными»

на экстремум являются те точки M0 ,

в которых

все частные производные первого порядка обращаются в нуль. Как и в случае функции одной переменной, такие тачки называются стационарными (при

этом требуется, чтобы функция			f (x, y) была дифференцируемой в точке M0 ).
Стационарные точки функции	f (x, y) можно найти,						решив систему уравнений
	/	(x, y) = 0,
fx		(x, y) = 0,						(1)
f /		(x, y) = 0.						(1)
	y

Пример 1. Найти стационарные точки функции
	z = x3 −3x + y4 −2 y2 .
Решение. Система (1) имеет вид
			/	= 3x	2	−3 = 0,
	zx			= 3x		−3 = 0,
	z/			= 4 y3 −4 y = 0.
			y
						x = ±1. Из второго
Из первого уравнения находим						x = ±1. Из второго		уравнения находим
y = 0, ±1. Следовательно, функция				z = x3 −3x + y4 −2 y2			(рис.	1.21, а) имеет шесть
стационарных точек: (1;0) , (1;−1) ,			(1;1) ,		(−1;0) , (−1;−1) , (−1;1) .

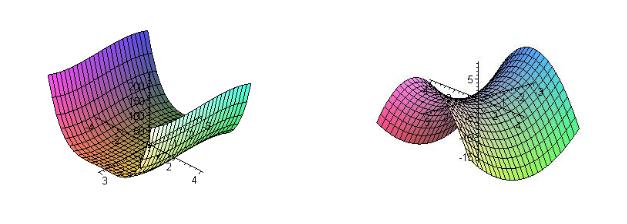
105

2. Условия теоремы 1 не являются достаточными условиями существования экстремума.

Например, для функции f (x, y) = x2 − y2 (рис. 1, б) частные производные

первого порядка равны нулю в точке (0;0), однако эта точка не является точкой локального экстремума. Действительно, в любой окрестности точки (0;0) существуют точки вида (x;0) , в которых f (x,0) > f (0,0) . Поэтому (0;0) не

является точкой локального максимума. Аналогично в любой окрестности точки (0;0) существуют точки вида (0; y) , в которых f (0, y) < f (0,0) . Поэтому

(0;0) не является точкой локального минимума.

а)	б)
Рис. 1. Графики функций: а)	z = x3 −3x + y4 −2 y2 , б) z = x2 − y2

Теорема 2 (достаточные условия экстремума). Пусть функция z = f (x, y) имеет непрерывные частные производные второго порядка в некоторой окрестности стационарной точки M0 (x0 , y0 ) . Положим

)

∆ =

(M0 )

0 )

= fxx

0 ) fyy

0 ) − fxy

0 ) .

fxy

fyy

Тогда:		∆ > 0 ,	то в точке M0 функция имеет локальный экстремум, причем
1)	если
при	fxx// (M0 ) < 0 – локальный максимум, а при fxx// (M0 ) > 0 – локальный минимум;
2)	если ∆ < 0 ,		то в точке M0 нет экстремума;
3)	если	∆ = 0 ,	то в точке M0 экстремум может быть, а может и не быть, и

необходимы дополнительные исследования. Пример 2. Найти экстремумы функции

z = x4 + y4 −2x2 + 4xy −2 y2 .

Решение. Найдем частные производные первого порядка zx/ = 4x3 −4x +4 y = 4(x3 − x + y) , zy/ = 4( y3 + x − y) .

Стационарные точки найдем, решая систему уравнений

x3 − x + y = 0,

y3 + x − y = 0.

106

Сложив уравнения системы,

получим

x3 + y3

= 0 , откуда

y = −x .

Подставив

y = −x

в первое уравнение системы,

придем к уравнению

x3 −2x = 0 . Получим

корни:

x1 = 0 , x2 =

2 , x3

= − 2 . Отсюда

следует, что y1 = 0 , y2 = −

2 , y3

2 .

Итак, наша функция имеет три стационарные точки:

M1 (0;0) ,

M2 ( 2;−

2 ),

M3 (− 2; 2 ).

Чтобы найти определитель ∆(x, y) , рассчитаем частные производные

второго порядка:

fxx// =12x2 −4 ,

fxy// = 4 ,

fyy// =12 y2 −4 .

Получим

∆(x, y) =

12x2 −4

=16

3x2 −1

=16(9x2 y2

−3x2 −3y2 ).

12 y2 −4

3y2 −1

Вычислим величину ∆(x, y) в стационарных точках:

∆(M1 )= 0 , ∆(M2 )= 384 > 0 ,

∆(M3 )= 384 > 0 .

Так как ∆(M2 )= 384 > 0 и

fxx// (M2 )= 20 > 0 ,

то,

согласно теореме 2, M2 ( 2;−

2 ) –

точка локального минимума (как и точка M3 (−

2; 2 )).

Рассчитаем

значение функции

z = x4 + y4 −2x2 +4xy −2 y2 (рис.

2) в

этих

точках:

zmin,1 = z (

2 )= −8 ,

zmin,2 = z (− 2; 2 )= −8 .

2;−

Так

как

∆(M1 )= 0 , поэтому в точке

теорему 2 применить нельзя.

Убедимся, что в этой точке экстремум отсутствует. Действительно,

если

y = 0 ,

то z = x4 −2x2

= x2 (x2 −2) < 0 в окрестности точки M1 . Если

y = x , то

z = 2x4

> 0 .

Итак, в окрестности точки M1 значения

z могут быть как положительные,

так

и отрицательные,

а это

означает, что

точка

M1 не является экстремальной.

Отметим, что других экстремумов заданная функция не имеет, поскольку точки, в которых производные zx/ и zy/ не существуют, отсутствуют.

а) б)

Рис. 2. График функции z = x4 + y4 −2x2 +4xy −2 y2 : а) обычный вид, б) вид снизу

107

3. Пусть функция z = f (x, y) определена и непрерывна в некоторой окрестности точки M (x; y) ; lG = (cosα;cos β) – единичный вектор; L – направленная прямая, проходящая через точку M ; M1 (x +∆x; y +∆y) – точка на прямой L (рис. 3); ∆l – величина отрезка MM1 ; ∆z = f (x +∆x; y +∆y) − f (x, y) – приращение функции f (x, y) в точке M (x; y) .

Рис. 3. Иллюстрация производной по направлению

Определение 2. Предел отношения

∆z

при ∆l → 0 ( M1 → M ), если он существует,

∆l

называется производной функции z = f (x, y)

в точке M (x; y)

по направлению вектора

(кратко – производная по направлению) и обозначается:

∂z

= lim

∆z .

∂l

∆l→0

∆l

Производная по направлению вычисляется по формуле:

∂z =

∂z cosα

∂z cos β

∂l

∂x

∂y

где cosα и cos β

– направляющие косинусы вектора l

. Ее физический смыслG– скорость

изменения функции в точке по направлению вектора l . Действительно, если l

= (1;0) ,

то

α = 0°, β = 90° и

∂z =

∂z . Если же l = (0;1) , то

∂z =

∂z . Т.о., производная по направлению

∂l

∂x

∂l

∂y

обобщает понятие частной производной.

z = x2 + y2 x

M (1; 2)

Пример 3. Вычислить производную

функции

точке

по

JJJJJG

направлению вектора MM1 , где M1 (3;0) .

Решение. Найдем единичный вектор l , имеющий данное направление:

JJJJJG

JJJJG

1 G

2i −2 j

MM1 = (2; −2)

= 2i

−2 j

;

MM1

= 2

2 ;

l =

JJJJJG1

i −

j .

MM1

Следовательно, cosα =

и cos β = −

Вычислим частные производные в точке M (1;2) :

fx/ (x; y) = 2x + y2 ;

fy/ (x; y) = 2xy ;

fx/ (1; 2) = 6 ; fy/ (1; 2) = 4 .

108

Окончательно получим:

∂z	= 6	1	−4	1	= 2 .
∂l		2		2

4. Важным понятием математического анализа является градиент.

Определение 3. Градиентом функции z = f (x, y) в точке M (x; y) называется вектор,

координаты которого равны соответствующим частным производным ∂∂xz и ∂∂yz , взятым в точке M (x; y) :

grad z = ∂∂xz ; ∂∂yz .

Его физический смысл – указывать направление наискорейшего роста функции, а максимальная скорость равна модулю градиента.

Пример 4. Найти градиент функции z = x2 +2 y2 −5 в точке M (2; −1) . Решение. Сделав все расчеты, получим:

∂z	= 2x ;	∂z	= 4 y ;	∂z		= 4 ;	∂z	= −4 ;	grad z = (4; −4).

∂x		∂y		∂x	(2;−1)		∂y	(2;−1)

109

Лекция 4. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

План

1.Суть метода наименьших квадратов.

2.Расчет параметров линейной функциональной зависимости методом наименьших квадратов.

1. Перед исследователем часто стоит задача нахождения количественной связи y = f (x) между данными эксперимента x1 , x2 ,..., xn и y1 , y2 ,..., yn . Функцию y = f (x) называют

моделью эксперимента.

Наиболее применим для этой цели метод наименьших квадратов (МНК). Его открыли на рубеже 18 и 19 веков независимо друг от друга Гаусс и Лежандр. Поводом для этого послужили практические потребности в астрономии и геодезии. Позже Д. И. Менделеев применял МНК для описания температурных и иных зависимостей свойств химических веществ. В начале 20 в. Пирсон обосновал применение МНК для проблем статистики. С 20-х г. 20 в. он широко используется в экономике – для эконометрических задач. МНК используют в психологии, педагогике, социологии, медицине. Широчайшее применение метод нашел во время Второй мировой войны в научных исследованиях, экономическом анализе и промышленном производстве. А начало массового выпуска в 50-е г. 20 в. ЭВМ вообще привело к повсеместному использованию МНК.

Для применения МНК в конкретном случае необходимо задать определенный вид функции f . Из каких же соображений выбирают тип кривой y = f (x) ? Часто этот вопрос

решается следующим образом: на график наносятся данные в виде точек с координатами

(xi ; yi ), i =1,2,..., n . Совокупность этих	точек в	системе	координат называют
корреляционным полем. Тип функции f	можно	определить	по внешнему виду

экспериментальной зависимости (рис. 1). Часто же бывает так, что теоретические сведения подсказывают тип кривой y = f (x) .

Рис. 1. Корреляционное поле и график функциональной зависимости

Например, если ищут функцию зависимости объема выпуска продукции z от затрат труда x и затрат производственных фондов y , то знания из области экономики

подсказывают, что такая зависимость скорее всего имеет вид производственной функции Кобба-Дугласа:

z = a0 xa1 y1−a1 ,

110

где a0 и a1 – параметры функции, которые определяются по конкретным экономическим

данным.
Рассмотрим на	рис. 1 данные	эксперимента, которые характеризуются точками
(xi ; yi ), i =1,2,..., n .,	и точки графика функциональной зависимости (xi ; f (xi )), i =1,2,..., n .
Разности	ui = yi	− f (xi ), i =1,2,..., n
	ui = yi	− f (xi ), i =1,2,..., n

называются отклонениями экспериментальных данных yi от расчетных данных модели

f (xi ) .

Если точка экспериментальных данных (xi ; yi ) принадлежит графику y = f (x) , то yi = f (xi ) . В этом случае ui = 0 , т.е. величина отклонения равна нулю. Если точка оказывается выше графика, то ui > 0 , ниже – следовательно ui < 0 . Рассмотрим сумму квадратов отклонений

∑ui2 = u12 +u22 +... +un2 . i=1

Суть МНК состоит в следующем. Необходимо найти такую функцию y = f (x) , чтобы сумма квадратов отклонений экспериментальных данных yi от расчетных данных модели f (xi ) была наименьшей.

2. Часто встречающийся на практике случай, когда предполагаемая зависимость между данными эксперимента x1 , x2 ,..., xn и y1 , y2 ,..., yn является линейной.

В этом случае функция связи ищется в виде

y = ax +b .

Линейная функция полностью определяется своими параметрами – коэффициентом наклона a и ординатой b точки пересечения с осью Oy .

Поставим перед собой цель: найти методы расчета параметров линейной функциональной зависимости с помощью МНК.

Запишем сумму квадратов отклонений

n	n	n
∑ui2 = ∑( yi − f (xi ))2 = ∑( yi −axi −b)2
i=1	i=1	i=1

и рассмотрим ее как функцию двух переменных a и b , т.е.

ϕ(a,b) = ∑( yi −axi −b)2 .

i=1

Чтобы сумма квадратов отклонений была наименьшей, нужно найти точку экстремума функции ϕ(a,b) . Необходимым условием точки экстремума функции многих переменных

является равенство нулю ее частных производных:

∂∂ϕa = 0;∂ϕ = 0.∂b

Имеем:

	n
	∑( yi −axi −
i=1

	n
	∑( yi −axi −

i=1

	/	n	/	n	n

b)2 = ∑ ( yi −axi −b)2				= ∑2( yi −axi −b)(−xi ) = −2∑( yi −axi −b)xi = 0;
a		i=1	a	i=1	i=1
	/	n	/	n	n

b)2 = ∑ ( yi −axi −b)2				= ∑2( yi −axi −b)(−1) = −2∑( yi −axi −b) = 0.
b		i=1	b	i=1	i=1

111

n	n	n		n	n	n	n
∑( yi −axi −b)xi = ∑xi yi −∑axi2 −				∑bxi = ∑xi yi −a∑xi2 −b∑xi = 0;
i=1	i=1	i=1		i=1	i=1	i=1	i=1
n	n	n	n	n	n
∑( yi −axi −b) = ∑yi −∑axi −∑b = ∑yi −a∑xi −bn = 0.
i=1	i=1	i=1	i=1	i=1	i=1
Тогда общая система уравнений для нахождения параметров a и b имеет вид:
	a∑xi 2		+b∑xi = ∑xi yi ,
		n	n	n
		i=1	i=1	i=1
		n		n
	a∑xi +bn =			∑yi .
		i=1		i=1
		n	n	n	n
Подставив в систему значения ∑xi ,			∑yi ,	∑xi2 ,	∑xi yi	, которые высчитаны на основе
		i=1	i=1	i=1	i=1

экспериментальных данных, мы решим ее относительно неизвестных a и b . Поставленная цель достигнута.

Пример 1. Предприятие имеет большое число филиалов, и его руководство хотело бы знать, имеется ли между показателем y (годовой товарооборот одного филиала, млн. грн.) и

показателем x (торговая площадь, тыс. м2) линейная зависимость:

№ филиала	1	2	3	4	5	6	7	8	9	10
Значения x	0,3	1	1,2	1,3	1,1	1,5	0,8	0,9	1,3	0,5
Значения y	2,9	5,3	6,9	7	7	8,4	4,3	5,8	7,7	3,2

По экспериментальным данным, используя МНК, найти уравнение прямой y = ax +b и

объяснить его смысл. Построить корреляционное поле и нанести на нём полученную прямую.

Решение. Составим расчётную табл. 1:

				Табл. 1. Расчётная таблица

i	xi	yi	xi 2	xi yi
1	0,3	2,9	0,09	0,87
2	1	5,3	1	5,3
3	1,2	6,9	1,44	8,28
4	1,3	7	1,69	9,1
5	1,1	7	1,21	7,7
6	1,5	8,4	2,25	12,6
7	0,8	4,3	0,64	3,44
8	0,9	5,8	0,81	5,22
9	1,3	7,7	1,69	10,01
10	0,5	3,2	0,25	1,6
	n	n	n	n
n =10	∑xi = 9,9	∑yi = 58,5	∑xi 2 =11,07	∑xi yi = 64,12
	i=1	i=1	i=1	i=1

Система уравнений для нахождения параметров a и b имеет вид:

11,07a +9,9b = 64,12,9,9a +10b = 58,5.

Решая ее, получим
11,07a +9,9(5,85 −0,99a) = 64,12,		1,269a = 6,205,		a ≈ 4,8897,
	−0,99a.		−0,99a.
b = 5,85	−0,99a.	b = 5,85	−0,99a.	b ≈1,0092.

112

Искомое уравнение прямой:

y = 4,8897x +1,0092 .

Оно имеет следующий смысл: с ростом торговой площади x на 1 единицу (т.е. на 1 тыс. м2) годовой товарооборот филиала y увеличивается в среднем на 4,8897 единиц (т.е. на

4,8897 млн. грн.).

В завершение, построим корреляционное поле и нанесем на нём полученную прямую

(рис. 2).

Рис. 2. Корреляционное поле и график линейной зависимости из примера 1

113

I I I.г ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

Лекция 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

План

1.Понятие первообразной и неопределенного интеграла.

2.Свойства неопределенного интеграла.

3.Таблица основных интегралов.

1. В дифференциальном исчислении мы решали следующую задачу: дана функция y = f (x) , найти ее производную y = f / (x) . В математике и ее приложениях часто возникает обратная задача: дана функция y = f (x) , найти функцию y = F(x) такую, что F / (x) = f (x) .

Таким образом, кроме операции дифференцирования, нужна еще и другая, которая сводится к операции нахождения функции по ее производной. Такая операция называется интегрированием [інтегруванням], а раздел математики, изучающий методы нахождения функции по ее производной, – интегральным исчислением [інтегральним численням]. Этот термин ввел Я. Бернулли в 1690 г. Этот термин связан с латинскими словами: integro – восстанавливать (т.е. по производной восстановить исходную функцию) и integer – целый.

Определение 1. Функция y = F(x) называется первообразной [первісною] функции y = f (x) на промежутке X , если для любого x X выполняется равенство

						F / (x) = f (x) .
	Например,				f (x) = cos x , тогда за первообразную можно взять F(x) = sin x , поскольку
(sin x)/ = cos x . Пусть						f (x) = x2 , тогда в качестве первообразной можно взять F(x) =			x3	, так
(sin x)/ = cos x . Пусть										, так
				/				3
			3	/
как		x		= x2 .	Заметим, что в первом случае		мы	могли вместо sin x в качестве
как				= x2 .	Заметим, что в первом случае		мы	могли вместо sin x в качестве
	3
первообразной взять,						например, F1 (x) = sin x +π	или	F2 (x) = sin x −200 , поскольку и

(sin x +π)/ = cos x , и (sin x −200)/ = cos x .

Теорема 1 (об общем виде первообразной). Если F(x) – первообразная для функции y = f (x) на промежутке X , то все первообразные для функции

y = f (x) имеют вид F(x) +C , где C – произвольная постоянная.
Доказательство. Пусть	F(x) – первообразная для f (x) .	Тогда	выполняется
равенство F / (x) = f (x) . Для любой постоянной C
(F(x) +C)/ = F / (x) +0 = f (x) ,
а это означает, что F(x) +C – также первообразная для f (x) .
Обратно, пусть наряду с данной первообразной F(x) функция F1 (x) – также
первообразная для f (x) . Тогда выполняются равенства
	F / (x) = F / (x) = f (x) ,
	1
откуда (F (x) − F(x))/ = 0 . Тогда	разность этих двух первообразных	будет	тождественно
1

равна константе:

F1 (x) − F(x) = C , или F1 (x) = F(x) +C ,

что завершает доказательство теоремы.

Эта теорема позволяет ввести основное понятие интегрального исчисления.

114

Определение 2. Если F(x) – первообразная для f (x) , то выражение F(x) +C , где C

– произвольная постоянная, называется неопределенным интегралом [невизначеним інтегралом] функции f (x) .

Неопределенный интеграл обозначается ∫ f (x)dx (читается «интеграл эф от икс дэ икс»). Таким образом,

∫ f (x)dx = F(x) +C .

Знак ∫ называют знаком интеграла, функцию f (x) – подынтегральной функцией, f (x)dx – подынтегральным выражением, C – постоянной интегрирования. Таким образом,

символ ∫ f (x)dx обозначает множество всех первообразных данной функции.

Нахождение функции по ее производной или, что то же, отыскание неопределенного интеграла по данной подынтегральной функции называется интегрированием данной функции. Интегрирование является операцией, обратной дифференцированию. Для того, чтобы проверить, правильно ли выполнено интегрирование, надо взять производную от полученного результата и убедиться, что получена подынтегральная функция.

2. Как всякая обратная операция, интегрирование – более сложное действие, чем дифференцирование. Мы приступаем к рассмотрению свойств неопределенного интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

(∫ f (x)dx)/ = f (x) , d ∫ f (x)dx = f (x)dx .

Действительно,

(∫ f (x)dx)/ = (F(x) +C)/ = f (x) , d ∫ f (x)dx = (∫ f (x)dx)/ dx = f (x)dx .

2. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная, т.е.

∫dF(x) = F(x) +C .

Поскольку dF(x) = F / (x)dx , то ∫dF(x) = ∫F / (x)dx = F(x) +C .

3. Постоянный множитель можно вынести из-под знака неопределенного интеграла, т.е.

∫kf (x)dx = k ∫ f (x)dx .

4. Неопределенный интеграл от суммы функций равен сумме интегралов от слагаемых, т.е.

∫( f1 (x) + f2 (x))dx = ∫ f1 (x)dx + ∫ f2 (x)dx .

Действительно, дифференцируя левую часть равенство, получим по свойству 1 (∫( f1 (x) + f2 (x))dx)/ = f1 (x) + f2 (x) , а производная правой части

(∫( f1 (x)dx + f2 (x))dx)/ = (∫ f1 (x)dx)/ +(∫ f2 (x)dx)/ = f1 (x) + f2 (x) ,

так что производные равны, что и требовалось проверить.

3. Приведем таблицу основных интегралов. Часть формул этой таблицы непосредственно следует из таблицы производных. Интегралы, содержащиеся в этой таблице, принято называть табличными.

115

Таблица основных интегралов

∫dx = x +C

II.

∫xndx =

xn+1

+C,

a ≠ −1

n +1

III.

∫dx

= ln

IV.

∫ax dx =

+C ,

∫ex dx = ex +C

ln a

∫cos x dx = sin x +C

VI.

∫sin x dx = −cos x +C

VII.

∫

= tgx +C

VIII.

∫

= −ctgx +C

cos2 x

sin2 x

IX.

∫

= arcsin

∫

= 1 arctg

− x

+ x

∫

x −a

∫

x2 + k

XI.

+C,

a ≠ 0

XII.

= ln

x +

2 2

−a

x + a

x + k

Пример 1. Найти ∫

2 +33

+5 x

dx .

Решение. Разделим почленно числитель на знаменатель и применим сначала

свойства 3 и 4, а затем табличные интегралы II и III.

2 +33 x2 +5 x

−

∫

= 2∫x

2 dx +

3∫x

6 dx +

5∫ x =

−

= 2

+5ln

+C = −

+186 x

+5ln

+C.

−

Пример 2. Найти ∫

x4 + x2

Решение. Сначала преобразуем подынтегральную функцию

x2 +1− x2

−

x4 + x2

x2 (x2 +1)

x2 +1

Теперь запишем исходный интеграл как разность табличных интегралов II и X (при a =1 ):

−2

∫

= ∫x2

−∫

= ∫x

dx −∫

= − x

−arctgx +C .

x4 + x2

x2 +1

Пример 3. Найти ∫

cos 2x dx

sin2 xcos2 x

Решение. Используя формулу cos 2x = cos2 x −sin2 x , представим данный интеграл в

виде разности табличных интегралов VIII и VII:

cos 2xdx

cos2 x −sin2 x

∫

=∫ sin2 xcos2 x dx

=∫

−∫

= −ctgx −tgx +C .

sin2 xcos2 x

sin2 x

cos2 x

116

Лекция 2. МЕТОДЫ ИНТЕГРИРОВАНИЯ

План

1.Интегрирование методом замены переменной.

2.Метод интегрирования по частям.

1. Если неопределенный интеграл удается найти с помощью его свойств и таблицы основных интегралов, то такой метод обычно называют методом непосредственного интегрирования

[методом безпосереднього інтегрування]. Этим методом, в частности, были решены примеры 1-3 из предыдущей лекции. В интегральном исчислении применяются и другие методы.

Во многих случаях введение новой переменной позволяет упростить подынтегральное выражение и свести интеграл к линейной комбинации табличных. Такой метод называется методом замены переменной [методом заміни змінної]. Он основан на следующей теореме.

Теорема 1. Пусть функция x =ϕ(t) определена и дифференцируема на

промежутке T	и X	– множество ее значений, на котором определена функция
f (x) . Тогда если		F(x) – первообразная для	f (x) на X , то F(ϕ(t)) –
первообразная	для	f (ϕ(t))ϕ/ (t) на T , т.е. на	множестве T выполняется

равенство

∫ f (x)dx		x=ϕ(t ) = ∫ f (ϕ(t))ϕ/ (t)dt .	(1)

Доказательство. По правилу дифференцирования сложной функции производная левой части равенства

Ft / (ϕ(t))= Fx/ (ϕ(t)) ϕ/ (t) = f (ϕ(t)) ϕ/ (t) ,

что совпадает с подынтегральной функцией в правой части равенства (1).

Формула (1) называется формулой замены переменной в неопределенном интеграле.

Пример 1. Найти ∫

dx .

+ x

Решение. Для того, чтобы избавиться от иррациональности, выполним замену

переменной x = t2 , t =

x . Тогда dx = 2tdt и наш интеграл примет вид

x = t

t 2tdt

1+t2

−1

dx =

= 2

dt = 2

dt −

∫1+ x

∫

1+t

∫ 1+t

∫1

dx =

2tdt

∫

= 2(t −arctgt) +C = 2(

x −arctg

x) +C.

Частным случаем теоремы 1 является следующая теорема, часто используемая на практике (линейная замена переменной).

Теорема 2. Если ∫ f (x)dx = F(x) +C , то

∫ f (ax +b)dx = 1a F(ax +b) +C .

Доказательство. Положим t = ax +b , тогда dt = adx , откуда dx = 1a dt , так что

∫ f (ax +b)dx = 1a ∫ f (t)dt = 1a F(t) +C = 1a F(ax +b) +C .

Пример 2. Найти ∫(2x +1)4 dx .

Решение. Можно, конечно записать подынтегральную функцию как многочлен от x , возведя 2x +1 в четверную степень, но это будет нерационально, поскольку проще выполнить линейную замену (см. теорему 2):

∫(2x +1)4 dx = 12 ∫(2x +1)4 d(2x +1) =12 (2x5+1)5 +C = (2x10+1)5 +C .

117

Пример 3. Найти ∫2xdx+5 .

Решение. Воспользуемся табличным интегралом III: ∫dxx = ln x +C . Тогда

∫2xdx+5 = 12 ln 2x +5 +C .

Формулой замены переменной (1) пользуются и справа налево. Тогда этот метод называют «внесением функции под знак дифференциала».

Пример 4. Найти ∫tgxdx .

Решение. Имеем ∫tgxdx = ∫sin x dx = −∫	d(cos x)	= −ln	cos x	+C .


cos x	cos x

2. Метод интегрирования по частям [метод інтегрування частинами] основан на формуле дифференцирования произведения двух функций.

Теорема 3. Пусть u(x) и v(x) – две дифференцируемые функции на промежутке X . Тогда на X выполняется формула интегрирования по частям:

∫udv = uv −∫vdu .

(2)

Доказательство. Имеем формулу для дифференциала произведения функций uv : d(uv) = udv +vdu . Интегрируя обе части равенства, получим слева uv по свойству 2 неопределенного интеграла, а справа сумму интегралов, так что

uv = ∫udv + ∫vdu ,

откуда легко получается формула (2).

Эта формула позволяет свести нахождение неопределенного интеграла ∫udv к

неопределенному интегралу ∫vdu , который может оказаться более простым.

Пример 5. Найти ∫xcos xdx .

Решение. Положим u = x , dv = cos xdx . Тогда du = dx , а функция v находится

интегрированием v = ∫cos xdx ,	так что можно положить v = sin x . Подставляем в формулу
(2), получим
u = x	du = dx
		= x sin x −∫sin xdx = x sin x +cos x +C .
∫xcos xdx =		= x sin x −∫sin xdx = x sin x +cos x +C .
dv = cos xdx	v = ∫cos xdx = sin x

Пример 6. Найти ∫ln xdx .

Решение. Используя формулу (2), получим

u = ln x

∫ln xdx = du = dx

dv = dx				dx
	= ln x x −	∫	x	dx	= xln x − x +C .
	= ln x x −		x		= xln x − x +C .
v = ∫dx = x				x

Иногда метод интегрирования по частям приходится комбинировать с методом замены переменной, как в случае интегрирования элементарной функции y = arcsin x .

Пример 7. Найти ∫arcsin xdx .

Решение. Имеем

118

u = arcsin x
	dx
∫arcsin xdx =
du =
	1− x	2

= arcsin x x + 12 ∫(1− x2 )−1/ 2

dv = dx

xdx

d (1

− x

)

= arcsin x x −

= arcsin x x +

v = x

∫

1− x2

∫ 1

− x2

(

)

1 (1− x2 )1/ 2

− x

= arcsin x x +

+C = arcsin x x +

1− x +C.

d 1

119

Лекция 3. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ КЛАССОВ ФУНКЦИЙ

План

1.Интегрирование рациональных функций.

2.Интегрирование тригонометрических функций.

1. Рассмотрим интеграл вида ∫R(x)dx , где R(x) – это рациональная функция, т.е. функция,

которую можно записать в виде отношения двух многочленов: R(x) = QP((xx)) .

Если эта дробь неправильная, т.е. степень многочлена P(x) не меньше степени многочлена Q(x) , то можно выполнить деление с остатком и представить R(x) в виде суммы некоторого многочлена и правильной дроби.

Пример 1. Найти ∫

−4

Решение. Рациональная

функция R(x) =

–

неправильная дробь,

поэтому

x2 −4

сначала мы должны выполнить деление с остатком:

x2 −4

x3 −4x

Т.е.

подынтегральную

функцию

можно представить

виде

= x +

. Таким

x2 −4

образом, получим

d (x2 −4)

∫

x3dx

∫xdx + ∫

4xdx

= ∫xdx + 2∫

+C .

2ln

−4

x2 −4

В курсе алгебры доказывается следующая важная теорема.

Теорема 1. Всякая правильная дробь может быть представлена в виде

суммы простейших дробей вида

Mx + N

, n ≥ 2 ,

x −a

(x −a)n

x2 + px +q

(x2 + px + q)n

где

A, M , N,a, p, q – действительные числа,

а трехчлен x2 + px +q

действительных

корней не имеет, т.е.

p2 −4q < 0 .

Пример 2. Найти ∫ x32 +4 dx . x −4x

Решение. Разложим знаменатель подынтегральной рациональной функции на множители: x3 −4x = x(x2 −4) = x(x −2)(x + 2) . Согласно теореме 1 правильная дробь должна разлагаться в сумму простейших дробей

	x2 +4	=	A	+	B		+		C		.
	x3 −4x		x		x −	2		x +		2

Найдем коэффициенты A, B,C . Воспользуемся						для			этого приемом, который называют

методом неопределенных коэффициентов. А именно, приведем правую часть равенства к общему знаменателю и приравняем числители:

x2 +4 = A(x −2)(x + 2) + Bx(x + 2) +Cx(x −2) = x2 ( A + B +C) + x(2B −2C) −4A .

Приравнивая коэффициенты при степенях переменной x , получим систему уравнений:

120

	A + B +C =1						C =1

	2B −2C = 0					B =1
		= 4
	−4A	= 4					A = −1
Таким образом, искомое разложение на простейшие дроби имеет вид:
	x2 +4	=	−1	+		1		+	1	,
	x3 −4x	=	x	+	x −2			+	x + 2	,
	x3 −4x		x		x −2				x + 2

так что интеграл представляется в виде суммы интегралов, которые легко находятся

x2 +4

∫

dx = ∫

+ ∫

= −ln

+ln

x −2

+ln

x + 2

+C .

x3 −4x

x −2

x + 2

Пример 3. Найти ∫ x32 +4x2 + 4 dx . x −2x + x

Решение. Разложим знаменатель на множители

x3 −2x2 + x = x(x2 −2x +1) = x(x −1)2 .

Согласно теореме 1 подынтегральная функция разложится на сумму простейших дробей:

x2 + 4x + 4	=	A	+	B	+	C	.
x3 −2x2 + x		x		x −1		(x −1)2

Так же, как в примере 2, приведем правую часть равенства к общему знаменателю и приравняем числители

x2 +4x + 4 = A(x −1)2 + Bx(x −1) +Cx = x2 ( A + B) + x(−2A − B +C) + A .

Решая систему уравнений, получим

+ B =1

= −3

= 9

−2A − B +C = 4

= 4

Таким образом, искомое разложение на простейшие дроби имеет вид

x2 + 4x + 4

−3

x(x −1)2

x −1

(x −1)2

так что интеграл равен сумме интегралов

x2 + 4x + 4

∫

dx = 4∫ x −3∫

+9∫

= 4ln

−3ln

x −1

−

+C .

x(x −1)2

x −1

(x −1)2

x −1

Пример 4. Найти ∫

x(x2 +1)2

Решение. Рациональная дробь

–

правильная и ее

разложение на

x(x2 +1)2

простейшие дроби, согласно теореме 1, имеет вид

Bx +C

Dx + E

x(x2 +1)2

x2 +1

(x2 +1)2

Сравнивая числители дробей в обеих частях равенства, получим

1 = A(x2 +1)2 +(Bx +C)x(x2 +1) +(Dx + E)x = x4 ( A + B) + x3C + x2 (2A + B + D) + x(C + E) + A .

Сравнивая коэффициенты при одинаковых степенях x в левой и правой частях, получим систему уравнений для нахождения неопределенных коэффициентов:

121

A + B = 0

B = −1

C = 0

+ D = 0

2A + B

D = −1

C + E = 0

E = 0

A =1

Искомое разложение имеет вид

−x

= 1

x(x2 +1)2

x2 +1

(x2 +1)2

Следовательно,

xdx

∫

=∫

−∫

x(x2 +1)2

x2 +1

(x2 +1)2

Второй и третий интеграл справа находим

одинаковой заменой t = x2 +1, dt = 2xdx , и

окончательно получим

∫

= ln

−

2 ln(x

+1) +

+C .

x(x2 +1)2

2(x2 +1)

2. Рассмотрим методы интегрирования тригонометрических функций.

Для этих целей часто используют универсальную тригонометрическую подстановку.

Спомощью такой замены переменной интегралы вида

∫R(sin x,cos x)dx ,

где R – некоторая рациональная функция, приводятся к интегралу от рациональной функции, и, следовательно, к ним можно применить метолы, рассмотренные в предыдущем пункте.

А именно, воспользуемся формулами, выражающими синус и косинус через тангенс

половинного аргумента		x				x
	2tg	x			1−tg2	x
	2tg				1−tg2	2
sin x =	2			, cos x =		2	, −π < x <π .
sin x =			x	, cos x =			, −π < x <π .
	1+tg2		x		1+tg2	x
	1+tg2		2		1+tg2	2
			2			2

Если мы положим t = tg

, то выражая

через t ,

получим x = 2arctgt , dx =

2dt

Поэтому

1+t2

∫

1−t

2dt

R(sin x,cos x)dx =

1+t

Таким образом, задача свелась к интегрированию рациональной функции. Разумеется, после нахождения интеграла справа нужно вернуться к переменной x , т.е. положить t = tg 2x .

Пример 5. Найти ∫

8 −4sin x +7cos x

Решение. Применим универсальную подстановку:

∫

= ∫

2dt

= ∫

2dt

8 −4sin x +7 cos x

8 −4

1−t2

1+t2

−8t +15

+t2

1+t2

= ∫

2dt

t −4 −1

+C = ln

t −5

+C.

= 2 2 ln

t −4 +1

t −3

(t −4)2 −1

122

Здесь мы воспользовались табличным

интегралом XI. Подставляя t = tg

окончательно получим

−5

∫

= ln

+C .

8 −4sin x +7cos x

−3

Иногда, исходя из вида подынтегральной функции, проще воспользоваться другой заменой.

cos3 x

Пример 6. Найти∫sin4 x dx .

t = sin x . Числитель подынтегрального

Решение. Выполним замену переменной

выражения можно представить следующим образом

t = sin x

−3

−1

cos x dx

∫

1−t

dt =

dt −

∫

t−4 dt

−

∫

t−2 dt = t

− t

+C .

∫sin4 x

dt = cos x dx

∫t4

∫t2

−3

−1

Возвращаясь к переменной x , получим

cos3 x

∫sin4 x dx

−

+C .

sin x

3sin3 x

Пример 7. Найти ∫

sin2 x −4sin xcos x +5cos2 x

Решение. Имеем

∫

= ∫

d(tgx)

sin2 x −4sin xcos x +5cos2 x

cos2 x(tg2 x −4tgx +5)

tg2 x −4tgx +5

Теперь ясно, что удобно выполнить замену переменной t = tgx . Интеграл примет вид

∫t2 −dt4t +5 = ∫(t −2)dt2 +1 = arctg(t −2) +C .

Таким образом,

∫sin2 x −4sin xcos x +5cos2 x = arctg(tgx −2) +C .

123

Лекция 4. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

План

1.Задача о вычислении площади криволинейной трапеции.

2.Понятие определенного интеграла.

3.Свойства определенного интеграла.

4.Формула Ньютона-Лейбница.

1. Пусть задана непрерывная неотрицательная функция y = f (x) на отрезке [a,b]. Криволинейной трапецией называется фигура aABb на плоскости Oxy , ограниченная вертикальными прямыми x = a и x = b , осью Ox и графиком функции y = f (x) (рис. 1).

Рис. 1. Криволинейная трапеция

Как найти площадь этой трапеции? Напомним, что при вычислении площади круга в школьном курсе математики поступают следующим образом. Рассматривают вписанные и описанные правильные многоугольники с увеличивающимся числом сторон и вычисляют их площадь, и затем принимают за площадь круга предел площадей этих многоугольников. По сути этот метод, используемый еще со времен Архимеда и известный как «метод исчерпывания», применим и в данной ситуации.

Разобьем	отрезок	[a,b]	на	мелкие	части	точками	деления
a = x0 < x1 < x2 <	... < xn−1 < xn = b .	Затем	найдем	на каждом	отрезке	разбиения	[xk , xk +1 ]

наименьшее значение функции y = f (x) , обозначим его mk и построим прямоугольник с

основанием [xk , xk +1 ] и высотой mk . Его площадь: Sk = mk (xk +1 − xk ) = mk ∆xk . Объединение всех таких прямоугольников даст ступенчатую фигуру, «вписанную» в

криволинейную трапецию aABb , обозначим ее площадь sT , где T обозначает выбранное разбиение отрезка [a,b] (рис. 2).

Рис. 2. Ступенчатая фигура, «вписанная» в криволинейную трапецию

124

Ясно, что S – площадь криволинейной трапеции aABb – будет не меньше площади вписанной ступенчатой фигуры sT для любого разбиения T : sT ≤ S .

Если же на каждом отрезке T выбрать наибольшее значение Mk функции y = f (x) ,

то поступая аналогичным образом, получим ступенчатую фигуру, «описанную» вокруг криволинейной трапеции aABb . Площадь этой фигуры обозначим ST (рис. 3).

Рис. 3. Ступенчатая фигура, «описанная» вокруг криволинейной трапеции

Очевидно, что для любого разбиения T отрезка [a,b] выполняется двойное

неравенство:

sT ≤ S ≤ ST .

Интуитивно ясно, что если разбиения T сделать достаточно мелкими, то площади вписанной и описанной ступенчатых фигур будут мало различаться. Поэтому естественно за площадь криволинейной трапеции S принять число, которое не меньше площади любой вписанной ступенчатой фигуры и не больше площади любой описанной ступенчатой фигуры. В рассматриваемом случае такое число должно быть единственным.

Понятно также, что искомая площадь S приближенно						равна площади вписанной или
описанной ступенчатой		фигуры:	S ≈ sT	или	S ≈ ST ,	причем	точность	равенства
увеличивается с измельчением разбиения				T . На практике отрезок			[a,b] разбивают на n
равных частей,	вместо	обозначения sT		используют соответственно sn , вместо ST
соответственно	Sn . Разность Sn −sn		определяет		точность.	Чем больше n ,		тем выше

точность. Проще всего число точек удваивать и проверять на каждом шагу: достигнута ли искомая точность. Точное равенство получится, если в приближенном равенстве перейти к пределу

S = lim sn	или S = lim Sn .
n→∞	n→∞

2. Построения, рассмотренные в предыдущем пункте, показывают, что решение таких и многих аналогичных им задач приводит к построению нижних и верхних сумм, соответственно sT и ST , для подходящего разбиения T данного отрезка, и нахождению

числа, разделяющего множества {sT } и {ST } . Рассмотрим данную задачу в общем виде. Итак, пусть на отрезке [a,b] дана ограниченная функция y = f (x) . Рассмотрим

разбиение T отрезка [a,b] точками деления

a = x0 < x1 < x2 <... < xn−1 < xn = b ,

на каждом отрезке разбиения [xk , xk +1 ] найдем нижнюю и верхнюю грани значений функции y = f (x) , соответственно, mk и Mk , и составим две суммы: нижнюю сумму Дарбу

	125
n−1	n−1
sT = ∑mk ∆xk	и верхнюю сумму Дарбу ST = ∑Mk ∆xk . На рис. 2, 3 этим суммам
k =0	k =0

соответствуют площади «вписанной» и «описанной» ступенчатых фигур. Эти суммы обладают следующими свойствами:

1. Для любого разбиения T выполняется неравенство sT ≤ ST , т.е. для данного

разбиения нижняя сумма Дарбу не превосходит верхней суммы.

Это следует из того, что для любого k справедливо неравенство mk ≤ Mk .

2. Если разбиение T2 получается из разбиения T1 добавлением нескольких новых точек, то sT1 ≤ sT2 и ST1 ≤ ST2 , т.е. при измельчении разбиения нижние суммы Дарбу могут

только увеличиваться, а верхние суммы только уменьшаться.

3. Для любых разбиений T1 и T2 выполняется неравенство

sT1 ≤ ST2 ,

или любая нижняя сумма Дарбу не превосходит любой верхней суммы Дарбу.

Из свойства 3 следует, что множество нижних сумм Дарбу X находится на числовой оси левее множества верхних сумм Дарбу Y , поэтому существует хотя бы одно число I ,

разделяющее множества	X и Y , т.е. для любого разбиения T		отрезка [a,b] выполняется
двойное неравенство	n−1	n−1
	n−1	n−1
	sT = ∑mk ∆xk ≤ I ≤ ∑Mk ∆xk = ST .
	k =0	k =0	отрезке [a,b], называется
Определение 1.	Функция y = f (x) ,	ограниченная на	отрезке [a,b], называется

интегрируемой [інтегрованою] на этом отрезке, если существует единственное число I , разделяющее множества нижних и верхних сумм Дарбу для всевозможных разбиений

отрезка [a,b]. Если функция y = f (x) интегрируема на отрезке [a,b], то единственное число, разделяющее эти два множества, называют определенным интегралом [визначеним інтегралом] функции y = f (x) по отрезку [a,b] и обозначают следующим образом

I = ∫b f (x)dx .

Знак определенного интеграла читается «интегралом от a до b », числа a и b

называют нижним и верхним пределами интегрирования [нижньою і верхньою границями інтегрування]. Обозначения были введены немецким ученым Г.Лейбницем, который вместе с И.Ньютоном был создателем дифференциального и интегрального исчислений. Лейбниц

ввел знак интеграла ∫ в виде вытянутой буквы S , которая обозначает знак суммирования. Самым замечательным результатом интегрального исчисления является формула Ньютона –

Лейбница, которая устанавливает связь между определенным интегралом ∫b f (x)dx и

неопределенным интегралом ∫ f (x)dx , что делает оправданным употребление знака

интеграла в обоих случаях.

Геометрический смысл определенного интеграла. Определенный интеграл дает площадь криволинейной трапеции (рис. 1), ограниченной вертикальными прямыми x = a , x = b при a < b , осью Ox и графиком неотрицательной и непрерывной функции y = f (x) .

3.Определенный интеграл имеет следующие свойства.

1.∫b f (x)dx = −∫a f (x)dx .

126

2. ∫a f (x)dx = 0 .

3. Функция, непрерывная на отрезке [a,b], интегрируема на этом отрезке.

4. Пусть функция y = f (x) интегрируема на отрезках [a,c] и [c,b], a < c < b . Тогда она интегрируема на отрезке [a,b], и выполняется равенство

∫b	f (x)dx = ∫c	f (x)dx + ∫b	f (x)dx .
a	a	c

5. Пусть дана функция y = f (x) , непрерывная на отрезке [a,b]. Тогда на этом отрезке найдется точка c , такая, что выполняется равенство

∫b

f (x)dx = f (c)(b −a) ,

число f (c) =

∫b

f (x)dx называют

средним значением функции [середнім значенням

b −a a

функції] f (x)

на отрезке [a,b].

6. Интеграл от суммы двух функций

f1 (x) и

f2 (x) по отрезку [a,b] равен сумме

интегралов от этих функций по тому же отрезку:

)

∫( 1

∫ 1

∫

(x)dx .

f (x) + f

(x) dx =

f (x)dx +

7. Постоянный множитель можно выносить из-под знака интеграла:

∫b kf (x)dx = k ∫b

f (x)dx .

8.Интеграл от неотрицательной функции на отрезке [a,b] – неотрицательное число,

т.е., если f (x) ≥ 0 на [a,b], то

					∫b	f (x)dx ≥ 0 .
			[a,b]		a
9.	Если	на отрезке	[a,b]	выполняется неравенство f (x) ≤ g(x) , то						такое	же
неравенство выполняется и для интегралов:
				∫b	f (x)dx ≤ ∫b g(x)dx .
		m – наименьшее,		a	M –			a
10.	Пусть	m – наименьшее,		а	M –			наибольшее значения непрерывной функции
y = f (x) на отрезке [a,b]. Тогда выполняется двойное неравенство
			m(b −a) ≤ ∫b				f (x)dx ≤ M (b −a) .
						a
4. Если функция		y = f (x) интегрируема на отрезке [a,b], то она интегрируема и на любом
меньшем	отрезке, и, для		любого	x [a,b]				существует интеграл ∫x	f (x)dx .	Чтобы	не
								a

смешивать обозначения верхнего предела и переменной интегрирования, будем записывать его в виде ∫x f (t)dt .

127

Определение 2. Для функции y = f (x) , интегрируемой на отрезке [a,b], интеграл

∫x f (t)dt ,

где x [a,b], называется интегралом с переменным верхним пределом [інтегралом із змінною верхньою границею].

Для каждого x [a,b] рассмотрим функцию Φ(x) = ∫x	f (t)dt . Оказывается, эта
a

функция является первообразной для y = f (x) , что мы и докажем в следующей теореме. Теорема 1 (о существовании первообразной для непрерывной функции). Если

функция y = f (x) непрерывна на отрезке [a,b], то функция Φ(x) = ∫x	f (t)dt
a

дифференцируема в любой точке этого отрезка, причем, Φ/ (x) = f (x) .

Иными словами, интеграл с переменным верхним пределом является первообразной

для непрерывной подынтегральной функции.

Φ(x) = ∫x

Доказательство. Будем искать производную функцию

f (t)dt , пользуясь

непосредственным определением производной, а именно

Φ/ (x) = lim Φ(x +∆x) −Φ(x) .

∆x→0

∆x

Для x (a,b) выберем ∆x столь малым,

чтобы точка

x + ∆x

лежала внутри отрезка

[a,b].

Тогда Φ(x +∆x) = x+∆∫x

f (t)dt .

Используя

свойство

для

определенного интеграла,

получим:

Φ(x +∆x) −Φ(x) = x+∆∫x

f (t)dt − ∫x

f (t)dt = ∫x

f (t)dt + x+∆∫x

f (t)dt −∫x

f (t)dt = x+∆∫x

f (t)dt .

К последнему интегралу применим свойство 5 о среднем для определенного интеграла:

Φ(x +∆x) −Φ(x) = x+∆∫x

f (t)dt = f (c)∆x ,

где промежуточная точка c находится между x и x + ∆x , поэтому

Φ(x +∆x) −Φ(x)

f (c)∆x

= f (c) .

∆x

Функция f (x) непрерывна.

∆x

При ∆x → 0

число c неограниченно приближается к

числу

x , т.е. c → x . Поэтому lim f (c) = f (x) . Следовательно,

∆x→0

Φ/ (x) = lim Φ(x +∆x) −Φ(x) = lim f (c) = f (x) .

∆x→0

∆x

∆x→0

Теорема доказана.

Докажем еще один основополагающий факт интегрального исчисления.

Теорема 2 (формула Ньютона – Лейбница). Пусть функция y = f (x) непрерывна на отрезке [a,b] и F(x) – первообразная для f (x) . Тогда

∫b f (x)dx = F(b) − F(a) .

Доказательство. Поскольку функция f (x) непрерывна на отрезке [a,b], то она интегрируема на этом отрезке и имеет первообразную на этом отрезке, а именно функцию

128

Φ(x) из предыдущей теоремы. Проверим справедливость формулы Ньютона – Лейбница для

этой первообразной. Т.к. Φ(x) = ∫x

f (t)dt ,

то подставляя

x = b , получим Φ(b) = ∫b

f (t)dt ,

подставляя x = a , получим Φ(a) = ∫a

f (t)dt = 0 . Поэтому

∫b

f (x)dx = Φ(b) −Φ(a) .

Если F(x) – другая первообразная для функции f (x) , то выполняется равенство

F(x) = Φ(x) +C .

Имеем

F(b) − F(a) = (Φ(b) +C) −(Φ(a) +C) = Φ(b) −Φ(a) = ∫b

f (x)dx .

Теорема доказана.

Разность F(b) − F(a)

часто

записывают

виде

F(x)

, и формула Ньютона

–

Лейбница в этом случае принимает следующий вид

∫b

f (x)dx = F(x)

= F(b) − F(a) .

Отметим еще два варианта данной формулы:

∫b F / (x)dx = F(b) − F(a) ,

∫b dF(x) = F(b) − F(a) .

Пример. Вычислить ∫2

x3dx .

Решение. По формуле Ньютона – Лейбница получим:

∫x

−

= 3,75 .

129

Лекция 5. МЕТОДЫ ОПРЕДЕЛЕННОГО ИНТЕГРИРОВАНИЯ

План

1.Метод замены переменной в определенном интеграле.

2.Метод интегрирования по частям в определенном интеграле.

3.Несобственные интегралы.

4.Приближенное вычисление определенных интегралов.

1. Сформулируем основной результат, позволяющий осуществлять замену переменной в определенном интеграле.

Теорема 1. Пусть функция y = f (x) непрерывна на отрезке [a,b], а функция x =ϕ(t) определена на отрезке [α, β] и имеет непрерывную производную внутри этого отрезка, причем ϕ(α) = a , ϕ(β) = b . Тогда

∫b	β
∫b	f (x)dx = ∫ f (ϕ(t))ϕ/ (t)dt .
a	α
Доказательство. Пусть F(x)	– первообразная для функции f (x) , тогда F / (x) = f (x) и

F(ϕ(t))/ = F / (ϕ(t)) ϕ/ (t) = f (ϕ(t)) ϕ/ (t) . Заметим, что из условий теоремы следует, что последняя функция интегрируема на отрезке [α, β]. Применяя формулу Ньютона-Лейбница, получим

(

))

(

)

(

))

(

))

∫

ϕ/

= F

− F

= F(b) − F(a) =

∫

f (x)dx .

t dt

Теорема доказана.

Пример 1. Вычислить ∫2

4 − x2 dx .

Решение.

Применим тригонометрическую замену переменной x = 2sin t ,

0 ≤ t ≤

π .

Преобразовав подынтегральное выражение, получим:

4 − x2

4 −4sin2 t = 2cos t , dx = 2 cos tdt .

π / 2

sin 2t

π / 2

∫

4 − x

= 2

π .

dx = ∫ 2cos t 2cos tdt = 2 ∫ (1+cos 2t)dt = 2 t

Подынтегральная функция

y =

4 − x2

– это уравнение верхней полуокружности с

центром в начале координат и радиусом 2 (рис. 1). Площадь данного сектора равна π кв.ед.

Рис. 1. Иллюстрация к примеру 1

130

2. Для определенного интеграла формула интегрирования по частям имеет следующий вид:

	b	b	b
	∫udv = uv	a	−∫vdu .
	a	a	a
Пример 2. Вычислить ∫e	x2 ln xdx .
1

Решение. Применим

		u = ln x,
e		u = ln x,
∫x2
∫x2	ln xdx =
1			2	dx,
	dv = x			dx,

формулу интегрирования по частям:

du = dx							e	e
	x				x	3	e		x	3
						3				3
			3	= ln x			1	−∫
		x	3	= ln x	3			−∫	3
2		x			3			1	3
v = ∫x	dx =

		3
		3

dx = e3 − x3 e = 2e3 + 1 . x 3 9 1 9 9

3. Вводя понятие определенного интеграла, мы предполагали, что отрезок интегрирования конечен, а подынтегральная функция ограничена на этом отрезке. В противном случае множество сумм Дарбу не будет ограниченным. Однако возможны случаи, когда одно или оба эти условия не выполняются. В таком случае соответствующие интегралы называются несобственными [невласними]. Мы будем различать два случая: 1) промежуток интегрирования бесконечен, или 2) подынтегральная функция не ограничена.

1) Начнем со случая, когда промежутком интегрирования является луч [a, +∞). Определение 1. Пусть функция y = f (x) интегрируема на каждом конечном отрезке

[a,b] ( b > a ), т.е. существует	определенный интеграл I (b) = ∫b		f (x)dx . Тогда за
		a
несобственный интеграл +∞∫ f (x)dx принимают предел
a
+∞∫	f (x)dx = blim→+∞ ∫b	f (x)dx .
a	a

Если предел lim ∫ f (x)dx существует и конечен, то говорят, что несобственный

b→+∞ a

интеграл сходится [збігається]. Если этот предел не существует или бесконечен, то несобственный интеграл расходится [розбігається].

По аналогии можно рассмотреть несобственный интеграл с бесконечным нижним пределом, а именно,

∫b	f (x)dx = alim→−∞ ∫b	f (x)dx .
−∞	a

Наконец, можно рассмотреть несобственный интеграл с бесконечными нижним и

верхним пределами ∞∫ f (x)dx . Для этого возьмем произвольную точку c . Она разобьет

−∞

числовую ось на два луча (−∞,c] и (c, +∞]. Если существуют несобственные интегралы

∫c f (x)dx и +∞∫ f (x)dx , то говорят, что существует и несобственный интеграл ∞∫ f (x)dx . В

−∞	c		−∞
этом случае полагают
	∞∫ f (x)dx = ∫c		f (x)dx + +∫∞ f (x)dx .
	−∞	−∞	c

Правая часть формулы не зависит от выбора промежуточной точки c .

131

Геометрический смысл несобственного интеграла. Пусть дана неотрицательная функция y = f (x) , непрерывная на луче [a, +∞). Для каждого b > a определенный интеграл

∫b	f (x)dx	дает площадь криволинейной трапеции aABb . Мысленно перемещая отрезок Bb
a
вправо,		мы получим в качестве значения несобственного интеграла	+∞∫ f (x)dx площадь
			a

«треугольника» aA∞ (рис. 2).

Рис. 2. Геометрический смысл несобственного интеграла

∞∫dx

Пример 3. Найти несобственный интеграл 1 x2 .

Решение. По определению 1 имеем

∞ dx

−2

= blim→∞

=1.

∫

= blim→∞ ∫x

dx = blim→∞ −

−

Таким образом, несобственный интеграл сходится и равен 1.

Пример 4. Найти несобственный интеграл ∞∫

Решение. Имеем

= lim b x−12 dx = lim 2

∞ dx

= lim

−4

= ∞.

b→∞

b→∞ (

)

∫

b→∞ ∫

Вданном случае несобственный интеграл расходится, т.к. предел равен бесконечности.

2)Рассмотрим теперь случай, когда подынтегральная функция не ограничена на отрезке интегрирования.

Пусть функция y = f (x) определена	на	промежутке [a,b). Точку x = b будем
называть особой [особливою], если функция	f (x)	не ограничена в любой окрестности этой

точки, но ограничена на любом отрезке, заключенном в промежутке [a,b) (рис. 3).

Рис. 3. Иллюстрация особой точки

					132
Определение 2. Пусть функция y = f (x)				не ограничена на отрезке [a,b],	однако
интегрируема на	любом	меньшем	отрезке [a,b −ε], где ε > 0 . Тогда, если существует
конечный предел	εlim→0+0 b∫−ε	f (x)dx , то его принимают за несобственный интеграл ∫b			f (x)dx
	a			a
от неограниченной функции f (x) .
Таким образом,		∫b	f (x)dx = εlim→0+0 b∫−ε
		∫b	f (x)dx = εlim→0+0 b∫−ε	f (x)dx .
		a	a

В этом случае говорят, что несобственный интеграл сходится. Если же предел не существует или бесконечен, то расходится.

Аналогично, если x = a – особая точка, то несобственный интеграл определяется так:

	∫b	f (x)dx =	εlim→0+0 ∫b	f (x)dx .
	a		a+ε
Если же x = c – единственная внутренняя особая точка на отрезке [a,b], то полагают
∫b	f (x)dx = ∫c		f (x)dx + ∫b		f (x)dx ,
a		a		c
при условии, что оба несобственных интеграла справа сходятся.
Если же особых точек на		отрезке	[a,b]	несколько, то отрезок интегрирования

разбивают таким образом, чтобы в каждом отрезке разбиения было не более одной особой точки, и используют определение 2.

Пусть F(x) – первообразная для функции f (x) . Положим F(a +0) = lim F(a +ε) ,

ε→0+0

F(b −0) = lim F(b −ε) , если эти пределы существуют. Тогда аналогом формулы Ньютона-

ε→0+0

Лейбница для сходящихся интегралов, у которых особыми точками являются только x = a и x = b , будет следующая формула:

∫b f (x)dx = F(b −0) − F(a +0) .

В случае же непрерывной функции F(x) на отрезке [a,b] получим формулу, полностью

совпадающую с формулой Ньютона-Лейбница:

∫b f (x)dx = F(b) − F(a) .

Пример 5. Найти интеграл ∫1 dx .

0 x

Решение. Подынтегральная функция f (x) = 1x имеет единственную особую точку

x = 0 на отрезке интегрирования [0,1]. Первообразной для этой функции будет F(x) = 2 x , которая непрерывна на этом отрезке. Имеем:

Таким образом, данный несобственный интеграл сходится и равен 2.

Пример 6. Найти интеграл ∫1 dx .

0 x

133

Решение. Подынтегральная функция f (x) = 1x имеет на промежутке интегрирования

[0,1] единственную особую точку x = 0 . Первообразной для нее будет F(x) = ln x . Поэтому имеем

lim

1 dx

lim ln

lim (ln1−ln ε) = 0 −

lim ln ε = +∞.

∫0

ε→0+0

∫ε x

ε→0+0

Таким образом, данный несобственный интеграл расходится.

Имеется тесная связь между несобственными интегралами с бесконечными пределами интегрирования и интегралами от неограниченных функций. Покажем это на примере 6. Выполним замену переменной

t = 1

x =

, dx = − dt .

Верхний предел интегрирования 1

не изменится, а нижний предел интегрирования будет

равен +∞, поскольку lim

= +∞. Таким образом,

x→0+0

+∞ dt

+∞ dx

−

tdt

∫0

∫1 t

∫1

+∞∫

Поэтому последний несобственный интеграл с бесконечным верхним пределом также расходится.

4. Задача нахождения первообразной элементарной функции – это вторая знаменитая математическая проблема, которая неразрешима в общем случае (первой была задача решения алгебраических уравнений в радикалах). Оказалось, что очень многие элементарные функции не интегрируемы, т.е. первообразные таких функций не являются элементарными

функциями. Таковы, например, функции e−x2 , ln1x , sinx x , первообразные которых существуют

ииграют значительную роль в математике и ее приложениях. Свойства этих функций хорошо изучены, существуют подробные таблицы их значений, можно построить их графики

ит.п.

Таким образом, если первообразная от элементарной функции не является элементарной функцией, то говорят, что интеграл «не берётся» в элементарных функциях. Короткое название – неберущийся интеграл [інтеграл, що не береться].

Сказанное выше наводит на мысль о необходимости приближенных формул вычисления определенных интегралов. Основная идея получения этих формул состоит в замене подынтегральной функции на функцию более простого вида, например, многочлен, интеграл от которого находят непосредственно по формуле Ньютона-Лейбница.

Пусть требуется	вычислить	определенный	интеграл	∫b	f (x)dx , где	f (x) –
				a
интегрируемая функция на отрезке [a,b]. Разобьем отрезок интегрирования на 2n						равных
частей:
a = x0 < x1 < x2 <... < x2k −2		< x2k −1 < x2k <... < x2n−2 < x2n−1 < x2n = b .
На каждом отрезке [x2k −2 , x2k ], k =1,..., n , как на основании cd ,				построим прямоугольник
cCDd с высотой f (x2k −1 )	(рис. 4). Заметим, что f (x2k −1 )		– значение интегрируемой функции,

вычисленное в точке x2k −1 , которая является серединой отрезка [x2k −2 , x2k ].

134

Рис. 4. Приближение криволинейной трапеции прямоугольниками
Обозначим через h =	b −a	длину отрезка разбиения. Тогда абсциссы x		, 1 ≤ k ≤ n
			−1
	2n	2k
		x1 = a +h , x2k +1 = x2k −1 +2h , k =1,2,...,n −1 .
вычисляются последовательно:				Площадь

криволинейной трапеции aABb заменим на сумму площадей всех прямоугольников. Таким образом, определенный интеграл приближенно равен сумме:

∫b	f (x)dx ≈ f (x1 ) 2h + f (x3 ) 2h +... + f (x2n−1 ) 2h = 2h( f (x1 ) + f (x3 ) +...+ f (x2n−1 ))=
a

имеющихся

следующей

2n−1

2h∑ f (xk ).

k =1

Эту формулу называют формулой прямоугольников [формулою прямокутників]. Погрешность применения данной формулы не больше чем

∆ = (b −a2)2 M , 24n

где M – максимум значений модуля второй производной интегрируемой функции на данном отрезке.

Для получения приближенной формулы вычисления определенного интеграла более высокой точности, нежели формула прямоугольников, вписывают вместо прямолинейных

отрезков куски парабол.
Итак,	рассмотрим криволинейную		трапецию, ограниченную графиком функции
y = f (x) . Разобьем отрезок интегрирования [a,b]				на 2n равных частей точками:
	a = x0 < x1 < x2 <... < x2k < x2k +1 < x2k +2 <... < x2n−2 < x2n−1 < x2n = b .
Приближенная формула имеет вид:
b	b −a	(y0 + y2n +2(y2 +... + y2n−1 )+		+... + y2n−1 ))=	b −a	n−1
∫ f (x)dx ≈			4(y1			∑(y2k + 4 y2k +1 + y2k +2 ),
					6n
a	6n					k =0

где yk = f (xk ) , 0 ≤ k ≤ 2n .

Данная формула называется формулой Симпсона или формулой парабол. В формуле Симпсона значения функции f (x) в нечетных точках разбиения x1,..., x2n−1 имеют

коэффициент 4, в четных точках x2 ,..., x2n−2 коэффициент 2, в граничных точках –

коэффициент 1. Погрешность формулы не больше чем ∆ = (b −a)2 M , где M – наибольшее

2880n4

значение модуля четвертой производной данной функции на отрезке [a,b].

135

Лекция 6. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

План

1.Вычисление площадей с помощью определенного интеграла.

2.Вычисления объемов тел вращения с помощью определенного интеграла.

3.Вычисления длины кривой с помощью определенного интеграла.

1. Геометрический смысл определенного интеграла. Для непрерывной неотрицательной функции y = f (x) , заданной на отрезке [a,b], определенный интеграл от данной функции по данному отрезку дает площадь криволинейной трапеции aABb (рис. 1).

Рис. 1. Геометрический смысл определенного интеграла

Пример

Найти площадь

криволинейной

трапеции,

ограниченной графиком

функции y = sin

x на отрезке 0,

Решение. Записываем соответствующий определенный интеграл и вычисляем:

1−cos 2x

sin 2x

xdx =

dx =

(кв.ед).

S = ∫sin

∫

∫dx − ∫cos 2xdx =

x −

2 =

С помощью интеграла можно находить площади плоских фигур более сложного вида, нежели криволинейная трапеция. Рассмотрим фигуру, ограниченную слева прямой x = a , справа прямой x = b (a < b) , снизу графиком функции y = f1 (x) и сверху графиком функции

y = f2 (x) ( f1 (x) ≤ f2 (x)) (рис. 2).

Рис. 2. Нахождение площади плоской фигуры

136

Площадь фигуры A1 A2 B2 B1

можно вычислить следующим образом:

S = S

aA2 B2b

−S

aA1B1b

∫

(x)dx −

∫

f (x)dx =

∫(

(x) − f (x) dx .

)

y = x −2 и параболой

Пример 2. Найти

площадь фигуры, ограниченной

прямой

y = 4 − x2 .

Решение. Построим фигуру, площадь которой мы ищем (рис. 3). Найдем точки пересечения двух данных линий:

						y = x −2							x		= −3, x = 2
									− x2					1			2
						y = 4			− x2				y1 = −5, y2 = 0
Поэтому пределы интегрирования будут a = −3 ,															b = 2 . Таким образом,										2
S = 2	(	4 − x2			−	(x −2) dx =				2	(	6	− x		− x2 dx =				6x −		x2		−	x3		=
										2											x2			x3
										∫
∫							)			∫							)					2	3		−3
−3										−3												2	3		−3
=12 −2 −			8			−18 −	9	+		= 7			1	+	13	1	= 20	5	(e∂	2		).
=12 −2 −			3	−		−18 −	2	+	9	= 7			3	+	13	2	= 20	6	(e∂			).
			3				2						3			2		6

	Рис. 3. Иллюстрация к примеру 2
2. С помощью определенного интеграла можно вычислять объемы фигур.
Теорема 1. Пусть функция		y = f (x) непрерывна и неотрицательна на отрезке [a,b].
Тогда тело, которое образуется при вращении вокруг оси						Ox	криволинейной трапеции
aABb (рис. 4), имеет объем		V =π∫b [f (x)]2 dx .
		V =π∫b [f (x)]2 dx .
			a					[a,b]
Доказательство.	Выполним		разбиение	T		отрезка		[a,b]		точками
a = x0 < x1 < x2 <... < xn−1 < xn = b .		На	каждом отрезке		разбиения			[xi−1 , xi ]		построим
прямоугольник MNQP (рис. 4),		высота которого		MP = mi	равна наименьшему значению
функции y = f (x) на указанном отрезке. При вращении вокруг оси								Ox	прямоугольник
MNQP опишет цилиндр, объем которого будет равен v =πm2						∆x , где ∆x = x − x				.
				i	i	i	i	i	i−1

Сумма объемов всех таких цилиндров для данного разбиения запишется в виде:

vT =π∑mi2 ∆xi .

i=1

Если бы мы вместо наименьшего значения функции f (x) брали бы наибольшее значение, то получили бы сумму:

137

VT =π∑Mi2 ∆xi .

i=1

Содной стороны ясно, что при измельчении разбиения T обе эти суммы дают приближенное значение искомого объема V , а с другой стороны, эти суммы являются

нижней и верхней суммой Дарбу для функции	y =π [ f (x)]2 . Последняя функция
непрерывна, поскольку непрерывна функция y = f (x)	и, следовательно, интегрируема.
Теорема доказана.

Рис. 4. Нахождение объема тела вращения

Пример 3. Окружность единичного радиуса с центром в точке O(0;2)

вращается

вокруг оси Ox (рис. 5). Найти объем тела вращения. (Это тело называется тором).

Решение. Уравнение окружности имеет вид:

x2 +( y −2)2

=1. Выражая y

через x ,

получим уравнения кривых ABC и ADC , соответственно:

y = f (x) = 2 + 1− x2 ;

y = f

(x) = 2 − 1− x2 .

Объем тора можно представить в виде разности объемов тел, полученных от

вращения криволинейных трапеций EABCF и EADCF . Используя теорему 1, имеем:

V =π 1

[f (x)]2

dx −π 1

(x)]2 dx =π 1

2 +

1− x2 2 − 2 −

1− x2

2 dx = 8π

1− x2 dx =

∫

−1

x = sin t

dx = cos tdt

−1 ≤ x ≤1				π			π
−1 ≤ x ≤1				2			2	1+
	π		π	2	cos	2	2	1+
−	π	≤ t ≤	π	= 8π ∫	cos		tdt = 8π ∫
−	2	≤ t ≤	2	π			π
	2		2	− 2			− 2

cos 2t		sin 2t	π / 2	= 4π	2	(e∂	3	).

2	dt = 4π t +	2	−π / 2

Рис. 5. Иллюстрация к примеру 3

138

3. С помощью определенного интеграла можно рассчитывать длину кривой.

Дифференциал дуги гладкой кривой, заданной функцией y = f (x) , a ≤ x ≤ b , находят

по формуле dl =

dx . Поэтому длина дуги

1+ f

(x)

l = ∫

dx .

1+ f

(x)

Пример 4. Найти длину участка кривой y =

4 − x2

, 0 ≤ x ≤ 2 .

Решение.

Производная

данной

функции

равна

y/ = −

. Воспользовавшись

− x2

формулой длины дуги, получим:

4 − x2 + x2

l = ∫ 1

dx = ∫

dx = 2 arcsin

=π (ед).

− x

4 − x

4 − x2

Подынтегральная функция y =

– это уравнение верхней полуокружности с

центром в начале координат и радиусом 2 (рис. 6). Действительно, длина этого участка окружности составляет π ед.

Рис. 6. Иллюстрация к примеру 4

139

I I I.д РЯДЫ

Лекция 1. ЧИСЛОВЫЕ РЯДЫ

План

1.Сходимость числового ряда. Необходимый признак сходимости ряда.

2.Достаточные признаки сходимости рядов (радикальный и интегральный признаки Коши, признак сравнения, признак Д’Аламбера).

1.Пусть дана числовая последовательность a1 , a2 , a3 ,..., an ,.... Выражение вида

	∞
a1 + a2	+ a3 +... + an +... = ∑an	(1)
	n=1
называется числовым рядом или просто рядом. Числа a1 , a2 ,..., an		называются членами ряда,
число an с общим номером n	называется общим членом ряда.	Суммы конечного числа
первых членов ряда

S1 = a1 , S2 = a1 + a2 , S3 = a1 + a2 + a3 ,..., Sn = a1 + a2 + a3 +... + an

называются частичными суммами ряда (1). Так как число членов ряда бесконечно, то частичные суммы образуют числовую последовательность

S1 , S2 , S3 ,..., Sn ,... .

(2)

Ряд (1) называется сходящимся, если последовательность (2) его частичных сумм сходится к некоторому числу S . В этом случае число S называется суммой ряда (1). В противном случае ряд (1) называется расходящимся. В случае сходимости ряда (1) его сумму записывают в виде символического равенства

			∞
S = a1 + a2	+ a3 +...an +... или S = ∑an .
		{	n=1	}
Пример 1. Если в качестве	последовательности	{	n	}
Пример 1. Если в качестве	последовательности		a , n	=1, 2,3,...

бесконечную геометрическую прогрессию с первым членом, равным b ≠ 0 q , то получим ряд

∞

b +bq +bq2 +... +bqn−1 +... = ∑bqn−1 .

n=1

мы рассмотрим и знаменателем

(3)

При q <1 ряд (3) является сходящимся и его сумма равна S = 1 −b q . Например,

							1			1			1				∞		1 n		1
						1+		+				+		... = ∑					=				= 2 .
						1+		+				+		... = ∑					=			1	= 2 .
							2			4			8			n=1			2	1−		1
							2			4			8			n=1			2	1−		2
Пример 2. Рассмотрим ряд																						2
Пример 2. Рассмотрим ряд									1				1						1
									1		+		1		+... +				1		+....
							1 2				+		2 3		+... +			n(n +1)			+....
							1 2						2 3					n(n +1)
Так как	1	=	1	−	1	, то для n -ой частичной суммы ряда получаем выражение
Так как	n(n +1)	=	n	−	n +1	, то для n -ой частичной суммы ряда получаем выражение
	n(n +1)		n		n +1
						Sn =				1 1							1			1			1
							1		−				+			−			+... +			−		.
							1		−	2			+		2	−	3		+... +			−	n +1	.
										2					2		3			n			n +1

После раскрытия скобок все слагаемые, кроме первого и последнего, взаимно уничтожаются,

и в результате получаем S	n	=1 −	1	. Отсюда следует, что lim S	n	=1. Итак, ряд сходится и
			n +1
				n→∞

его сумма равна 1.

140

Теорема 1 (необходимый признак сходимости ряда). Если числовой ряд

(1) сходится, то предел его общего члена равен нулю:

lim an = 0 .

n→∞

Подчеркнем, что это только необходимое условие сходимости ряда, т.е. условие, при нарушении которого ряд не может сходиться. С помощью этого признака можно доказывать только расходимость ряда.

Пример 3. Исследуем на сходимость ряд

12 + 23 +... + nn+1 +... .

Имеем lim a	n	= lim	n	=1 ≠ 0 , поэтому данный ряд расходится.
Имеем lim a		= lim		=1 ≠ 0 , поэтому данный ряд расходится.
n→∞		n→∞ n +1
Пример 4. Рассмотрим т.н. гармонический ряд
				1+ 1	+ 1 +	1 +... +	1	+... .
				2	3	4	n

Очевидно, что для гармонического ряда выполнено необходимое условие сходимости, так

как lim a	n	= lim 1	= 0 . Тем не менее, в примере 6 будет показано, что гармонический ряд
n→∞	n	n→∞ n

является расходящимся. Рассчитаем пока несколько его частичных сумм:

S10 = 2,929; S100 = 5,187; S1000 = 7,485; S10000 = 9,788 .

Видно, что они медленно растут, не стремясь к какому-то конкретному пределу S .

2. В дальнейшем будут рассматриваться числовые ряды a1 +a2 +... + an +... , все члены

которых положительны.

Теорема 34.2 (критерий сходимости ряда). Для того, чтобы ряд с положительными членами (1) сходился, необходимо и достаточно, чтобы последовательность его частичных сумм (2) была ограничена.

Указанный критерий имеет, скорее, теоретическое, нежели практическое значение. Поэтому необходимо уметь использовать достаточные признаки сходимости ряда: радикальный и интегральный признаки Коши, признак сравнения, признак Д’Аламбера.

Теорема 34.3 (радикальный признак Коши). Если для ряда с

положительными членами (1) существует предел							lim n a = K , то при		K <1 ряд
							n→∞	n
							n→∞
сходится, при K >1 – расходится, при			K =1 вопрос о сходимости ряда остается
открытым.
Пример 5. Исследуем сходимость ряда					n
	∞		4n		n
	∑				.
	∑				.
	n=1	n +1
Для этого применим радикальный признак Коши:
lim n a = lim				4n		= 4 >1.
lim n a = lim						= 4 >1.
n→∞	n	n→∞ n +1
n→∞		n→∞ n +1
Следовательно ряд расходится.
Теорема 34.4 (интегральный признак Коши). Пусть задан ряд
					∞
f (1) + f (2) +... + f (n) +... = ∑ f (n) ,									(4)

n=1

члены которого являются значениями непрерывной, положительной и монотонно убывающей функции f (x) при x ≥1. Тогда ряд (4) будет

сходящимся, если будет сходящимся несобственный интеграл ∞∫ f (x)dx , т.е.

a1 +a2 +... + an +... , b1 +b2 +... +bn +... ,

141

∞∫ f (x)dx = A < ∞ , и расходящимся, если этот интеграл будет расходящимся, т.е.

∞∫ f (x)dx = ∞ .

Пример 6. Выясним, при каких α > 0 сходится ряд

+... +

+... .

(5)

Положим

f (x) =

( x ≥1). Данная функция монотонно убывает, поскольку ее производная

f / (x) = −

отрицательна.

Поэтому

по

теореме

4 сходимость ряда (5) эквивалентна

α+1

∞

сходимости несобственного интеграла ∫1 dxxα

. Заметим, что

∞

α ≠1;

1 ,

∞ dx

(1−α)xα−1

∫

∞

α =1.

Видно, что этот интеграл сходится при α >1 и расходится при 0 <α ≤1. Значит, и ряд (5) сходится при α >1 и расходится при α ≤1 . Так как при α =1 ряд (5) становится гармоническим

1+ 12 + 13 + 14 +... + 1n +... ,

то, согласно интегральному признаку Коши, он является расходящимся рядом.

Теорема 5 (признак сравнения). Пусть даны два ряда с положительными членами:

(6)

(7)

причем члены первого ряда не превосходят соответствующих членов второго: an ≤ bn ( n =1,2,...). Тогда из сходимости большего ряда (7) следует сходимость

меньшего ряда (6). Из расходимости меньшего ряда (6) следует расходимость большего ряда (7).

Замечание 1. Признак сравнения можно использовать и в том случае, когда неравенство an ≤ bn выполняется не для всех членов рядов (34.6) и (34.7), а начиная с

некоторого номера N .

Замечание 2. При исследовании рядов с помощью признака сравнения нужно знать, какие ряды сходящиеся и какие расходящиеся. Для сравнения удобно пользоваться рядами:

∞

cxo∂.,

<1,

∞

cxo∂., α>1,

1) ∑bqn−1

2) ∑

≥1;

n=1

pacxo∂.,

n=1

pacxo∂., α ≤1.

Пример 7. Исследуем сходимость ряда

∞

∑

n=1 n

						142
	1		1		∞	1
Так как	1	≤	1	,	n =1,2,..., и ряд ∑	1	– сходящийся как геометрическая прогрессия со
Так как	n	≤	n	,	n =1,2,..., и ряд ∑	n	– сходящийся как геометрическая прогрессия со
	n 3		3		n=1	3

знаменателем q = 13 <1, то, согласно признака сравнения, исследуемый ряд тоже является

сходящимся.

Теорема 6 (признак Д’Аламбера). Если для ряда с положительными членами a1 +a2 +... + an +... существует предел

lim

an+1

= D ,

(8)

n→∞

то ряд сходится

случае

D <1,

расходится

случае

D >1 и нуждается в

дополнительном исследовании при D =1 .

Пример 8. Исследуем сходимость ряда

+... +

+... .

Для того, чтобы применить признак Д’Аламбера, рассчитаем предел (8):

n+1

lim

= lim

n+1

= lim

lim 1+

<1 .

n→∞

n→∞ 2

n→∞

2 n→∞

Следовательно, ряд является сходящимся.

143

Лекция 2. СТЕПЕННЫЕ РЯДЫ

План

1.Знакопеременные ряды.

2.Степенные ряды.

3.Ряды Маклорена и Тейлора.

4.Разложение в ряды элементарных функцій.

5.Приближенные вычисления с помощью степенных рядов.

1.Ранее мы рассматривали только ряды с положительными членами. Рассмотрим теперь ряды с членами произвольного знака, или, как принято говорить, знакопеременные ряды.

Особенно часто среди знакопеременных рядов встречаются ряды, члены которых имеют чередующиеся знаки, т.е. знакочередующиеся ряды.

Условимся считать первый член ряда положительным; тогда знакочередующийся ряд в общем виде запишется так:

a −a	+ a −a	4	+... +(−1)n−1 a	n	+...	(1)
1 2	3	4		n

где все an положительны ( n =1,2,...).

Теорема 1 (признак Лейбница). Знакочередующийся ряд (1) сходится,

если его члены убывают по абсолютной величине a > a

> a >...

и lim a

= 0 .

1 2

n→∞

Например, сходимость ряда

(−1)n−1

1−

−

+... +

+... .

следует непосредственно из теоремы Лейбница.

Ряд называется знакопеременным [знакозмінним], если он содержит бесконечное

число как отрицательных, так и положительных членов. Рассмотрим такой ряд:

a1 +a2 +... + an +... .

(2)

Составим ряд из модулей:

+... +

+... .

(3)

Теорема 2 (признак сходимости знакопеременного ряда). Если ряд из модулей (3) сходится, то сходится и ряд (2). При этом (2) называют абсолютно сходящимся [абсолютно збіжним] рядом.

Заметим, что ряд (2) может сходится, а ряд из модулей (3) при этом расходится. В этом случае (2) называется условно сходящимся [умовно збіжним] рядом.

Например, знакопеременный ряд ∑∞ (−1)n – условно сходящийся. Действительно, по

n=1 n

теореме Лейбница он сходится, а ряд составленный из его модулей ∑∞ 1 расходится.

n=1 n

2. Ряд вида

a	+a x + a x2		+... + a xn +... ,	(4)
0	1	2	n

где a0 , a1 , a2 ,..., an ,... – некоторая числовая последовательность, называется степенным [степеневим] рядом. Числа a0 , a1 , a2 ,..., an ,... называются коэффициентами степенного ряда.

Придавая переменной x различные числовые значения, будем получать различные числовые ряды, которые могут сходиться или расходиться. Множество тех значений x , при которых ряд (4) сходится, называется областью сходимости [областю збіжності]. Область сходимости любого степенного ряда не пуста, поскольку очевидно, что ряд (4) сходится для x = 0 .

144

Теорема 3. Для степенного ряда (4) возможны только три случая:

1)ряд сходится в единственной точке x = 0 ;

2)ряд сходится для всех значений x ;

3)существует такое r > 0 , что ряд сходится для всех значений x из

интервала (−r, r) , и расходится для всех значений x вне отрезка [−r, r]. Интервал (−r,r) называется интервалом сходимости ряда (4), а число r – радиусом

сходимости этого ряда. Понятие радиуса сходимости будем распространять на все три

случая в теореме 3: в случае 1) r = 0 , в случае 2)

r = ∞ . Радиус сходимости степенного ряда

чаще всего находят с помощью признака Даламбера.

Теореме 4. Если существует предел

D = lim

an+1

, отличный от нуля, то

n→∞

радиус сходимости степенного ряда (4) равен:

r =

= lim

(5)

n→∞

an+1

Пример 1. Найти область сходимости ряда

+... +

+....

Решение. В данном случае a

= 1

, a

n+1

, поэтому

r = lim

n +1

= lim

= lim 1

=1.

n→∞

n+1

n→∞

Следовательно, по теореме 4 данный ряд сходится на интервале (−1,1) . Исследуем поведение ряда на концах интервала, т.е. при x = ±1. При x =1 получаем гармонический ряд, который

расходится. При x = −1 получаем знакочередующийся ряд −1+ 12 − 13 +... + (−n1)n +... , который

сходится по признаку Лейбница. Таким образом, областью сходимости данного степенного ряда является интервал [−1,1).

3. Для практических нужд важно уметь данную функцию f (x) разлагать в степенной

ряд.

Пусть функция f (x) определена в некоторой окрестности точки x = 0 и имеет в этой


точке производные всех порядков. Степенной ряд
f (x) = f (0) +		f / (0)	x +	f // (0)	x2 +... +	f (n) (0)	xn +...	(6)
				2!
1!						n!
называется рядом Маклорена для функции f (x) .
Теорема 5 (достаточное условие разложимости функции в ряд
Маклорена). Пусть функция f (x)				определена и бесконечно дифференцируема в
интервале (−r, r) . Если существует такая константа M , что								во всех точках
указанного интервала выполняются неравенства
	f (n) (x)		< M (n = 0,1,2,...) ,					(7)

то в этом интервале ряд Маклорена сходится к функции f (x) . Например, f (x) = ex . В любом интервале (−r,r) имеем

f (n) (x) = ex < er .

145

В силу теоремы 5 следует,

что

функция

равна сумме

своего

ряда Маклорена при

x (−r, r) , а значит, и для любого x ввиду произвольности r . Поскольку

f (n) (0) = e0 =1 при

любом n , то получаем разложение

=1+ x +

... +

+...,

справедливое для всех x .

Пусть функция

f (x)

определена в некоторой окрестности точки

x0 и имеет в этой

точке производные всех порядков. Степенной ряд

(n) (x )

f (x) = f (x

) +

f / (x )

(x − x )

f // (x )

(x − x

)2 +... +

(x − x )n +...

f (x) .

называется рядом Тейлора с центром x0

для функции

4. Приведем разложения некоторых элементарных функций в степенные ряды:

+ x +

+... +

+..., x R ,

sin x = x −

x2n+1

x R ,

−... +

(−1)

+... ,

(2n +1)!

cos x =1−

x2n

−... +(−1)

+... , x R ,

(2n)!

ln(1+ x) = x −

−

+... +(−1)

xn+1

+... , −1 < x ≤1 ,

n +1

arctgx = x

n x2n+1

−

−... +(−1)

+...,

≤1,

2n +

(1+ x)a =1+ a x + a(a −1) x2 + a(a −1)(a −2) x3 +... + a(a −1)...(a −n +1) xn +...,

<1.

1 2

1 2 3

5. Разложения функций в степенные ряды часто применяют в приближенных вычислениях.

Пример 2. Вычислить с точностью до 0,001 значение sin18° .

Решение. Заметим, что x =18°= 10π . Воспользуемся разложением функции sin x в ряд Маклорена:

sin

−

π5

−... .

103 3!

105 5!

Поскольку

> 0,001

> 0,001 ,

π5

< 0,001 , то с точностью до 0,001 имеем

103

105

sin18° ≈

−

π3

≈ 0,309 .

103 3!

Пример 3. Вычислить с точностью до 0,001 интеграл

1/∫3 e−x2 dx .

Решение. Формула Ньютона-Лейбница здесь не применима, так как первообразная от e−x2 в элементарных функциях не выражается (т.н. неберущийся интеграл). Воспользуемся разложением в ряд Маклорена функции ex :

146

Далее имеем

1/∫3 e−x2 dx =

Поскольку 13 > 0,001,

получим

e−x2 =1− x2 +

−

+... .

1/ 3

− x2 +

1/ 3

−

+... dx =

−

+...

5 2!

7 3!

∫0

−

+....

5 2! 3

3! 3

> 0,001,

< 0,001 , то с точностью до 0,001

2430

3 3

5 2! 3

1/∫3 e−x2 dx ≈ 1 −

≈

0,321.

147

ЧАСТЬ I V ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Лекция 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

План

1.Общие сведения о дифференциальных уравнениях.

2.Дифференциальное уравнение первого порядка. Задача Коши.

3.Дифференциальные уравнения с разделяющимися переменными.

1.Различные вопросы математики, естествознания, экономики приводят к необходимости решения уравнений, содержащих в качестве неизвестной некоторую функцию y(x) , наряду с которой в уравнении присутствуют и ее производные до некоторого

порядка n . С одним из наиболее простых таких уравнений, уравнением вида y/ = f (x) , мы

уже встречались в интегральном исчислении. Его решением является неопределенный интеграл от f (x) . Приведем другие примеры таких уравнений:

y/ +2 y = x2 ; y/// + y/ = 0 ; y// = xy .

Определение 1. Уравнение, связывающее независимую переменную x с неизвестной

функцией y(x) и ее производными до некоторого порядка n	включительно, называется
обыкновенным дифференциальным уравнением n -го порядка:
F(x, y, y/ , y// ,..., y(n) ) = 0 ,	(1)

где F – некоторая заданная функция, x – независимая переменная, y(x) – искомая функция, а y/ (x),..., y(n) (x) – ее производные.

Следовательно, наивысший порядок производной функции y(x) , входящей в

уравнение (1), определяет порядок дифференциального уравнения (ДФУ). Таким образом, приведенные выше уравнения являются примерами дифференциальных уравнений соответственно первого, третьего и второго порядков.

Определение 2. Решением дифференциального уравнения (1) называется любая функция y(x) , имеющая производные до n -го порядка включительно, и такая, что ее

подстановка в уравнение (1) обращает его в тождество. График решения y(x) называют

интегральной кривой.

Например, решением уравнения

y/ = 2 y

является функция y = e2 x . Легко видеть, что решением этого уравнения будет также любая функция вида

y(x) = Ce2 x ,	(2)
где C – произвольная константа.
Определение 3. Функция y =ϕ(x,C1 ,C2 ,...,Cn ) , содержащая	n независимых

произвольных постоянных, называется общим решением ДФУ (1), если она является его решением при любых значениях констант C1 ,C2 ,...,Cn . Придавая в

выражении y =ϕ(x,C1 ,C2 ,...,Cn ) конкретные значения постоянным C1 ,C2 ,...,Cn

получают частное решение ДФУ (1).

Следовательно, общим решением ДФУ (ОР ДФУ) y/ = 2 y будет функция

(2). Если же константе C придать конкретное значение (например, 5), то получим частное решение ДФУ (ЧР ДФУ) y = 5e2 x .

Подводя итоги сказанному выше, отметим следующие факты:

148

1) ДФУ имеет бесконечно много решений;

2)общее решение ДФУ зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения;

3)частные решения получаются из общего путем придания конкретного

значения этим постоянным.

Отметим также, что процесс нахождения решения ДФУ принято называть интегрированием этого уравнения. Геометрически общее решение ДФУ определяет в координатной плоскости семейство интегральных кривых, зависящих от параметров C1 ,C2 ,...,Cn (рис. 1).

Рис. 1. Семейство интегральных кривых ДФУ y/ = 2 y

2. Общий вид ДФУ первого порядка есть

F(x, y, y/ ) = 0 .
Если это уравнение можно разрешить относительно	y/ , т.е. записать в виде
y/ = f (x, y) ,	(3)

то говорят, что ДФУ записано в нормальной форме (или в форме Коши). Как мы уже отмечали выше, ДФУ имеет бесконечно много решений. Для

ДФУ первого порядка общее решение будет зависеть от одной константы C , т.е. иметь вид y =ϕ(x,C) .Чтобы из этого множества решений выделить какое-то конкретное решение, необходимо указать дополнительное условие. Чаще всего

такое условие задается в виде начального условия
y(x0 ) = y0 .	(4)

Определение 4. Задача о нахождении частного решения ДФУ (3), удовлетворяющего начальному условию (4), называется задачей Коши и записывается в виде:

y/ = f (x, y) ,

y(x0 ) = y0 .

Геометрический смысл решения задачи Коши состоит в том, что следует найти такую интегральную кривую ДФУ, которая проходит через заданную точку (x0 , y0 ) .

Например, рассмотрим задачу Коши

149

y/ = 2 y , y(0) = 3 .

Как указывалось ранее, общее решение этого ДФУ: y(x) = Ce2 x . Учитывая начальное условие y(0) = 3 , получим

3 = Ce2 0 C = 3.

Следовательно, решением данной задачи Коши будет частное решение ДФУ y(x) = 3e2 x .

Замечание. Для решения задачи Коши ДФУ n -го порядка следует задавать n начальных условий. Т.е. количество начальных условий определяется порядком ДФУ.

Например, для ДФУ третьего порядка, разрешенного относительно старшей производной, задача Коши формулируется следующим образом:

y/// = f (x, y, y/ , y// ) ,

y(x0 ) = y0 , y/ (x0 ) = y0/ , y// (x0 ) = y0// .

3. Одним из наиболее простых, но весьма важных с точки зрения приложений типов ДФУ являются уравнения с разделяющимися

переменными. Это ДФУ вида:
y/ = p(x) g( y) ,		(5)
где p(x) и g( y) – непрерывные функции.
Запишем уравнение (5) в форме
dy	= p(x)g( y) .
dx

Для отыскания решения этого уравнения необходимо, как говорят, разделить в нем переменные, т.е. переписать уравнение следующим образом:

gdy( y) = p(x)dx ,

в предположении, что в рассматриваемой области g( y) ≠ 0 . Теперь левая часть уравнения содержит только переменную y , а правая только x .

Интегрируя обе части последнего уравнения, получим общий интеграл уравнения (5):

∫gdy( y) = ∫p(x)dx .

Это равенство запишем в виде следующего соотношения:

G( y) = P(x) +C ,

где G( y) – какая-либо первообразная для g(1y) , а P(x) – первообразная для

p(x) .

Пример 1. Задано ДФУ

xy/ − y = 0 .

Требуется: 1) найти его общее решение; 2) решить задачу Коши при начальном условии y(−2) = −8 .

Решение. 1)

x dydx − y = 0 , xdy − ydx = 0 ,

			150
dy	− dx = 0	– ДФУ с разделяющимися переменными,
y	x
		dy	= dx ,
		y	x
		∫dy	= ∫dx ,
		y	x
		ln y = ln x +ln C ,
		y = Cx – ОР ДФУ.
2) Для решения задачи Коши учтем начальное условие y(−2) = −8 :
		−8 = C(−2) C = 4 ,
	y = 4x	– решение задачи Коши или ЧР ДФУ.

Пример 2. Население некоторой страны – непрерывная функция y = y(t) , зависящая от времени t , которое измеряется в годах. Динамика изменения населения задана ДФУ

dydt = 0,05y .

Через какое время население страны удвоится, если на данный момент оно составляет 1 млн. людей?

Решение. Для начала решим задачу Коши:

dydt = 0,05y , y(0) =1.

Имеем уравнение с разделяющимися переменными: dyy = 0,05dt ,

∫dyy = ∫0,05dt ,

ln y = 0,05t +ln C , y = Ce0,05t – ОР ДФУ.

Начальное условие задачи Коши y(0) =1, поэтому

1 = Ce0,05 0 C =1,

y = e0,05t – решение задачи Коши.

Следовательно, количество населения данной страны задается функцией y = e0,05t . Чтобы выяснить через какое время население страны удвоится, решим уравнение:

2 = e0,05t ,

0,05t = ln 2 ,

t = 0,05ln 2 = 20ln 2 ≈13,86 (лет).

Итак, для удвоения населения понадобится почти 14 лет.

151

Лекция 2. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

План

1.Линейные дифференциальные уравнения первого порядка.

2.Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.

3.Частные решения неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.

1. В предыдущей лекции мы изучали дифференциальные уравнения с разделяющимися переменными. Другим часто встречающимся типом являются линейные дифференциальные уравнения.

Определение 1. Дифференциальное уравнение вида

			α(x) y/ + β(x) y +γ (x) = 0			(1)
называется линейным дифференциальным уравнением первого порядка.
Если α(x) ≠ 0 ,			то линейное дифференциальное уравнение			(ЛДФУ) (1)
можно представить в виде:
				y/ + p(x) y = f (x) ,		(2)
где p(x) =	β(x)	; f	(x) = −	γ (x)	.

	α(x)		α(x)
Дифференциальное уравнение
				y/ + p(x) y = 0		(3)

называется линейным однородным уравнением, соответствующим уравнению (2).

Уравнение (2) – это уравнение с разделяющимися переменными. Действительно

dyy = −p(x)dx .

Интегрируя это уравнение, получим

ln y = −P(x) +ln C

где P(x) – произвольная первообразная для функции p(x) , а C –

положительная постоянная. Из последнего уравнения находим общее решение уравнение (3):

y = Ce−P( x) ,

где C – постоянная произвольного знака.

Одним из наиболее удобных методов решения уравнения (2) является

метод подстановки y(x) =u(x) v(x) .

Применим этот метод к уравнению (2). Получим

(u(x) v(x))/ + p(x) u(x) v(x) = f (x) ,

u/ (x) v(x) +u(x) v/ (x) + p(x) u(x) v(x) = f (x) , u/ (x) v(x) +u(x) v/ (x) + p(x) v(x) = f (x) .

Приравняем выражение в квадратных скобках к нулю и найдем одно из решений этого дифференциального уравнения. Тогда линейное дифференциальное уравнение (2) будет сведено к системе двух дифференциальных уравнений с разделяющимися переменными

	/	(x) + p(x) v(x)		= 0
v		(x) + p(x) v(x)		= 0
			f (x)	(4)
u/ (x) v(x) =			f (x)

152

Найдя из системы (4) функции u(x) и v(x) , запишем общее решение уравнения (2) как y(x) = u(x) v(x) .

Пример 1. Решить уравнение

y/ − 2xy = x2 cos x .

Решение. Данное уравнение – это ЛДФУ первого порядка (2). Применим метод подстановки y = uv :


u/ v +uv/	− 2 uv = x2 cos x ,
		x
u/ v +u v/ −			2	v = x2			cos x .
u/ v +u v/ −				v = x2			cos x .
			x
Составим систему (4):		2 v = 0
v/	−	2 v = 0
		x
/	v = x				2	cos x
u	v = x					cos x
Решим первое уравнение системы:
v/	−	2 v = 0 ,
			x

dvdx = 2x v , dvv = 2x dx ,

∫dvv = ∫2x dx , ln v = 2ln x +ln C ,

v = Cx2 .

Так как нам нужно одно ЧР ДФУ, то возьмем C =1. Имеем

v = x2

u/ x2 = x2 cos x

Решаем второе уравнение:

u/ x2 = x2 cos x , dudx = cos x ,

∫du = ∫cos xdx ,

u = sin x +C .

Итак, ОР ЛДФУ будет таким:

y = uv = (sin x +C)x2 .

Убедимся проверкой в правильности решения:

((sin x +C)x2 )/ − 2((sin x +C)x2 ) = x2 cos x , x

x2 cos x + 2x(sin x +C) −2x(sin x +C) = x2 cos x , 0 = 0 .

2. Рассмотрим линейное дифференциальное уравнение (ЛДФУ) второго

порядка с постоянными коэффициентами

	153
y// + py/ + qy = f (x) ,	(5)

где q, p – некоторые константы.

Уравнению (5) соответствует однородное ЛДФУ:

		y// + py/ + qy = 0 .	(6)
Пусть yop	–	ОР неоднородного уравнения (5),	yp – ЧР неоднородного
уравнения (5),	yoo	– ОР однородного уравнения (6).	Имеет место следующее
утверждение.

Теорема 1. Общее решение неоднородного уравнения (5) есть сумма общего решения соответствующего ему однородного уравнения (6) и частного решения неоднородного уравнения (5):

yop = yoo + yp .		(7)
Рассмотрим однородное ЛДФУ (6). Имеет место следующий результат.
Теорема 2. Пусть y1 (x), y2 (x)	– решения уравнения (6),	тогда их линейная
комбинация C1 y1 (x) +C2 y2 (x) , где	C1 ,C2 – произвольные	константы, также

является решением уравнения (6).

Ранее мы отмечали, что ОР ДФУ 2-го порядка зависит от двух

произвольных констант. Из теоремы 2 следует, что функция
y(x) = C1 y1 (x) +C2 y2 (x)	(8)

является решением уравнения (6). Возникает вопрос: может ли формула (8) определять ОР ДФУ (6). Если да, то при каких условиях? Чтобы разобраться в этом, введем несколько понятий, аналогичных сведениям из линейной алгебры.

Определение 2. Функции y1 (x), y2 (x) называются линейно

независимыми, если их линейная комбинация обращается в ноль, т.е.

C1 y1 (x) +C2 y2 (x) = 0 ,

только лишь в случае C1 = C2 = 0 . В противном случае они называются

линейно зависимыми.

Определение 3. Систему функций y1 (x), y2 (x) , состоящую из двух линейно

независимых решений уравнения (6), будем называть фундаментальным набором решений этого уравнения.

Имеет место следующий факт.

Теорема		3.	Пусть		y1 (x), y2 (x) – фундаментальный набор решений
уравнения (6), тогда ОР этого уравнения задается формулой:
					yoo = C1 y1 +C2 y2 .				(9)
Фундаментальный набор решений уравнения (6) находят методом
Эйлера в	виде	функций			y = eλx . Получаем	y/ = λeλx ,	y// = λ2eλx .		Подставляя
выражения для		y ,	y/	и y//	в уравнение (6), имеем
					λ2eλx + pλeλx +qeλx = 0 .
Так как eλx ≠ 0 ,				то это соотношение эквивалентно уравнению
					λ2 + pλ +q = 0 .				(10)
Определение				4.	Алгебраическое	уравнение		(10)	называется
характеристическим уравнением однородного ЛДФУ (6).
При	решении			характеристического уравнения			могут возникать три

случая.

Случай 1. Дискриминант D характеристического уравнения (10) больше нуля. Тогда существует два действительных и различных решения λ1 и λ2

154

кратности

Соответствующие

им

решения y

= eλ1x ,

= eλ2 x

образуют

фундаментальный набор и ОР уравнения (6) имеет вид

= C eλ1x +C

eλ2 x .

Пример 2. Решить уравнение

y// + y/ −2 y = 0 .

Решение. Корнями характеристического уравнения

λ2 +λ −2 = 0

являются

числа λ1 =1 и

λ2 = −2 . Следовательно,

ОР однородного

ЛДФУ

имеет вид

= C ex +C

e−2 x .

Проверкой можно убедиться в правильности решения.

Случай

2. Дискриминант D = 0 .

характеристического

уравнения

существует

единственный

действительный

корень

λ = −

кратности

2. Ему

соответствует решение y1 = eλx . Вторым решением из фундаментального набора будет функция y2 = xeλx .

Таким образом, ОР имеет вид

yoo = C1eλx +C2 xeλx = eλx (C1 +C2 x) .

Пример 3. Решить уравнение
	y// +6 y/ +9 y = 0 .
Решение. Характеристическое уравнение
	λ2 +6λ +9 = 0 ,
		(λ +3)2		= 0
имеет единственный действительный			корень λ = −3 кратности 2.				Поэтому
ОР имеет вид		= e−3x (C +C
y	oo	= e−3x (C +C				x) .
	oo		1		2
Проверкой можно убедиться в правильности решения.
Случай 3. Дискриминант D < 0 . Характеристическое уравнение имеет два
комплексных корня (их называют комплексно сопряженными)							λ =α ±iβ
кратности 1. Им соответствует фундаментальный набор решений
y = eαx	cos βx ,		y	2	= eαx sin βx .
1				2

В итоге, ОР будет таким:

yoo = C1eαx cos βx +C2eαx sin βx = eαx (C1 cos βx +C2 sin βx) .

Вернемся к комплексно сопряженным числам α ±iβ .		Здесь i = −1 –
мнимая	единица, α – действительная часть комплексного числа, β –
мнимая	часть комплексного числа. Комплексное число α +iβ	имеет простой

геометрический смысл. В координатной плоскости – это точка с координатами (α; β) . Числу α −iβ соответствует точка (α;−β) .

Пример 4. Решить уравнение

y// −4 y/ +29 y = 0 .

Решение. Рассмотрим характеристическое уравнение

λ2 −4λ +29 = 0 .

Его дискриминант D = −100 . Следовательно, корнями этого квадратного уравнения будут комплексно сопряженные числа:

155

λ = 4 ±	−100			= 4 ±	−1	100 =		4 ±i 10	= 2 ±i 5 .
	2				2			2
Поэтому ОР однородного ЛДФУ имеет вид
	y	oo	= e2 x (C cos5x +C				2	sin 5x) .
		oo			1		2
Проверкой можно убедиться в правильности решения.
3. Рассмотрим теперь неоднородное уравнение (5). Согласно теореме 1,
				yop = yoo + yp .
ОР однородного ЛДФУ	(6)			yoo	мы	научились			находить ранее. Теперь

следует предложить методы нахождения ЧР неоднородного ЛДФУ (5) yp .

Ограничимся случаем, когда правая часть уравнения (5) имеет специальный вид

f (x) = eαx (Pk (x)cosbx +Qn (x)sin bx) ,

где Pk (x) , Qn (x) – многочлены от x степени, соответственно, k и n . Для отыскания ЧР уравнения (5) воспользуемся методом неопределенных

коэффициентов.

Обозначим через

т.н. контрольное

число.

Результаты

поместим в

таблицу 1.

Табл. 1. Виды ЧР неоднородных ЛДФУ 2-го порядка с постоянными

коэффициентами

Вид правой

Контрольное число

Вид ЧР

части

f (x) = Pk (x)

γ = 0

= Mk (x) ;

γ = 0 не является корнем

характеристического

уравнения;

–

корень

= xs Mk (x) .

γ = 0

характеристического

уравнения кратности s .

f (x) = Pk (x) e

γ = a

γ = a не является корнем

= Mk (x) eax ;

характеристического

уравнения;

–

корень

= xs Mk (x) eax .

γ = a

характеристического

уравнения кратности s .

f (x) = Pk (x) eαx cosbx

γ = a ±ib

не является

= L (x) eαx cosbx +

αx

sin bx

γ = a ±ib

+Qn (x) e

корнем характеристического

αx

sin bx,

уравнения;

+Nm (x) e

где

m = max{k,n};

γ = a ±ib

–

корень

yp = xs [Lm (x) eαx cosbx

характеристического

+Nm (x) eαx sin bx].

уравнения кратности s .

156

Пример 5. Решить уравнение

y// +5y/ +6 y =10e5x .

Решение. Согласно (7), имеем

						yop = yoo + yp .
Рассмотрим для начала однородное уравнение
					y// +5y/ +6 y = 0 .
Запишем характеристическое уравнение:
Его корни λ1 = −3 и λ2			= −2 .		λ2 +5λ +6 = 0 .
Его корни λ1 = −3 и λ2			= −2 .	Следовательно, ОР однородного ЛДФУ имеет
вид				y		= C e−3x +C		e−2 x .
				y	oo	= C e−3x +C		e−2 x .
					oo	1	2
Воспользуемся таблицей 1. В нашем случае									a = 5 . Многочлен	Pk (x) =10
имеет	нулевую	степень.	Контрольное				число γ = 5		не совпадает с	корнями
λ1 = −3	и λ2 = −2	характеристического уравнения, поэтому ЧР будем искать в
виде yp = Mk (x) eax . В качестве				Mk (x) рассматриваем произвольный многочлен
нулевой степени		Mk (x) = A , где		A – неизвестная константа. Поэтому ЧР ищем
в виде	yp = Ae5x .
Находим yp / = 5Ae5x ,			yp // = 25Ae5 x . Подставляем в исходное уравнение:
			25Ae5 x +5 5Ae5x +6 Ae5 x =10e5x ,

56Ae5x =10e5x .

Применяем метод неопределенных коэффициентов: 56A =10 ,

A = 1056 = 285 .

Следовательно,

yp = 285 e5x .

Окончательно имеем

yop = C1e−3x +C2e−2 x + 285 e5x .

Пример 6. Решить уравнение

y// + y = x2 .

Решение. Согласно (7), имеем

yop = yoo + yp .

Рассмотрим для начала однородное уравнение y// + y = 0 .

Запишем характеристическое уравнение:

λ2 +1 = 0 .

Его корни λ1,2 = ±i . Следовательно, ОР однородного ЛДФУ имеет вид yoo = C1 cos x +C2 sin x .

Воспользуемся таблицей 1. Многочлен P (x) = x2 имеет вторую степень.
k
Контрольное число γ = 0 не совпадает с корнями	λ1,2 = ±i характеристического
уравнения, поэтому ЧР будем искать в виде	yp = Mk (x) . В качестве Mk (x)

157

рассматриваем произвольный многочлен второй степени

Mk (x) = Ax2 + Bx +C ,

где A, B,C – неизвестные константы. Поэтому ЧР ищем в виде yp

= Ax2 + Bx +C .

Находим yp /

= 2Ax + B ,

yp // = 2A .

Подставляем в исходное уравнение:

2A + Ax2 + Bx +C = x2 ,

Ax2 + Bx +(2A +C) = x2 .

Применяем метод неопределенных коэффициентов:

A =1

B = 0

2A +C = 0

C = −2

Следовательно,

yp = x2 −2 .

Окончательно имеем

= C cos x +C

sin x + x2 −2 .

Пример 7. Решить уравнение

y// −2 y/ + y = ex .

Решение. Согласно (7), имеем

yop = yoo + yp .

Рассмотрим для начала однородное уравнение

y// −2 y/ + y = 0 .

Запишем характеристическое уравнение:

λ2 −2λ +1 = 0 ;

(λ −1)2

= 0 .

Уравнение имеет единственный действительный корень

λ =1

кратности 2.

Поэтому ОР однородного ЛДФУ имеет вид

= ex (C +C

x) .

Воспользуемся таблицей 1. В нашем случае

a =1. Многочлен Pk (x) =1

имеет нулевую степень. Контрольное число

γ =1

совпадает с

корнем

λ =1

кратности

Следовательно,

ЧР

будем

искать

виде

yp = x2 Mk (x) ex

yp = Mk (x) eax .

качестве

Mk (x)

будем

рассматривать

произвольный

многочлен нулевой

степени

Mk (x) = A ,

где

–

неизвестная

константа. Поэтому ЧР ищем в виде

yp = Ax2ex .

Находим

yp / = 2Axex + Ax2ex

= (2Ax + Ax2 )ex ,

yp // = (2A +4Ax + Ax2 )ex .

Подставляем в исходное уравнение:

(2A +4Ax + Ax2 )ex −2(2Ax + Ax2 )ex + Ax2ex = ex ,

2Aex = ex ,

A = 12 .

Следовательно,

yp = 12 x2ex ,

158

yop = ex (C1 +C2 x) + 12 x2ex .

Окончательно имеем

y	op	= ex C		+C	x + 1 x2	.
	op		1	2	2
					2

159

ЗАКЛЮЧЕНИЕ

Представленный курс позволяет студенту любой формы обучения глубоко усвоить высшую математику. Лекционный материал является основой для изучения учебных дисциплин «Теория вероятностей и математическая статистика», «Оптимизационные методы и модели», «Эконометрия», спецкурсов по экономико-математическому моделированию.

Кроме теоретических сведений, лекции содержат информацию прикладного характера. Эти сведения могут быть полезны студентам при подготовке курсовых работ, дипломного проекта и научной деятельности.

160

ЛИТЕРАТУРА

1.Практикум по решению задач курса «Высшая математика»: Учебное пособие. Часть 1. Издание 2-е, переработанное и дополненное / Сост. Румянцев Н.В., Медведева М.И., Полшков Ю.Н., Пелашенко А.В. – Донецк: ДонНУ, 2011. – 216 с.

2.Практикум по решению задач курса «Высшая математика»: Учебное пособие. Часть 2 / Сост. Румянцев Н.В., Медведева М.И., Полшков Ю.Н., Пелашенко А.В. – Донецк:

ДонНУ, 2009. – 228 с.

3.Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике: Ч. 1. – М.: Финансы и статистика, 2000. – 224 с.

4.Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике: Ч. 2. – М.: Финансы и статистика, 1999. – 376 с.

5.Дубовик В.П., Юрик І.І. Вища математика. – К.: А.С.К., 2001. – 648 с.

6.Кудрявцев В.А., Демидович В.П. Краткий курс высшей математики. – М.: Наука, 1989. – 656 с.

7.Щипачев В.С. Высшая математика. – М.: Высш. шк., 1991. – 479 с.

8.Минорский В.П. Сборник задач по высшей математике: Учеб. пособие для втузов. – 13-е изд. – М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 352 с.

9.Тевяшев А.Д., Литвин А.Г. Высшая математика. Общий курс: Сборник задач и упражнений. – Харьков, ХТУРЭ, 1997. – 192 с.

10.Интернет-сайты: www.exponenta.ru; www.allmath.ru; mathem.h1.ru; mathproblem.narod.ru; www.nsc.ru/win/mathpub/math_www.html; allmath.com.ru и др.

11.Страница кафедры математики и математических методов в экономике Донецкого национального университета: http://ec.donnu.edu.ua/uk/metodichne-zabezpechennya

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1111

Соседние файлы в предмете Высшая математика

#
13.04.20154.9 Mб206Полшков Ю.Н. Курс лекций по высшей математике.pdf
#
13.04.20156.31 Mб211Практикум по высшей математике_часть 1.pdf
#
13.04.20157.85 Mб231Практикум по высшей математике_часть 2.pdf