
К решению задач по электричеству
.pdf
§1. Напряженность электростатического поля. Потенциал.
I. Краткие теоретические сведения
Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд.
Закон Кулона: Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с соединяющей эти заряды прямой.
F12 k qr1q22 e12 ,
где k – коэффициент пропорциональности, q1 и q2 – величины взаимодействующих зарядов, r – расстояние между ними, e12 – единичный вектор направленный от заряда 1 к заряду 2, F12 – сила, действующая на заряд 2 со стороны заряда 1.
Коэффициент k определяется следующим образом:
1 |
|
9 |
м |
||
k |
|
9 10 |
|
|
, |
4 0 |
|
|
|||
|
|
|
Ф |
||
где 0 = 8,85 10-12 Ф/м – электрическая постоянная.
Напряженность поля, создаваемого точечным зарядом q прямо пропорциональна заряду и обратно пропорциональна квадрату расстояния от заряда до данной точки поля:
|
|
1 |
|
q |
|
Е |
|
|
|
|
er , |
4 0 |
|
r2 |
|||
|
|
|
|
вектор направлен вдоль прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателе.
Принцип суперпозиции: напряженность поля системы зарядов равна векторной сумме напряженностей полей, создаваемых каждым зарядом в отдельности:
N
ЕEi .
i 1
Потенциал поля точечного заряда:
(r) k q . r
По принципу суперпозиции потенциал системы точечных зарядов равен:
|
1 |
|
N |
q |
|
(r) |
|
|
|
i |
. |
4 |
0 |
r |
|||
|
|
i 1 |
i |
||
II. Примеры решения задач
Пример 1.1. Тонкая проволока, представляющая по форме четверть кольца радиуса R, заряжена равномерно зарядом q. Найти напряженность поля в центре кривизны.
Решение.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выбираем на кольце элементарный |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
заряд dq |
2q |
|
|
dl , |
|
где |
dl Rd и d |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
dl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
- угол под которым из центра кри- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
визны виден элемент dl. Напряжен- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ность поля, создаваемого этим эле- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
dEx |
|
|
|
ментарным зарядом, равна: |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dE |
|
kdq |
|
k2qRd |
|
2kq |
d . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
R2 R |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
R2 |
||||||||||
|
|
|
|
dEy |
|
|
|
|
|
|
|
Введем оси координат и находим |
|||||||||||||||||||
|
|
|
|
|
|
Рис.1.dE1 |
|
|
|
проекции напряженности поля на |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выбранные оси: |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
dEx |
|
|
2kq |
|
cos d , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2kq |
|
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dEy |
|
|
|
sin d |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
2kq |
2kq |
2 |
|
2kq |
|
|
|
|
2kq |
|||||||||||||
E |
|
|
|
dE |
|
|
|
|
|
cos d |
|
|
|
cos d |
|
|
sin |
|
|
|
|
sin0 |
|
|
|
||||||
x |
|
x |
|
|
R2 |
|
|
|
|
|
|
R2 |
|||||||||||||||||||
|
|
|
|
R2 |
|
R2 |
2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2kq |
|
2kq |
2 |
|
2kq |
|
|
|
|
|
2kq |
||||
E |
|
|
|
dE |
|
|
|
|
sin d |
|
sin d |
|
|
cos |
|
|
cos0 |
|
. |
|||||
|
|
|
0 R2 |
|
|
|
|
|
|
|||||||||||||||
|
y |
|
|
|
y |
|
R2 |
0 |
|
R2 |
2 |
|
|
|
R2 |
|||||||||
|
|
|
|
А |
|
|
|
|
|
Тогда суммарная напряженность будет равна: |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2kq |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
|
|
|||||||
|
|
|
|
|
|
|
х |
|
|
|
|
E |
Ex Ey |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
||||||||||
r |
|
|
|
|
|
|
|
|
|
Вектор напряженности направлен под углом 45 к оси х. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
Пример 1.2 Находящейся в вакууме тонкий прямой стержень |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
длины 2а заряжен равномерно с зарядом q. Найти модуль |
||||||||||||||
анапряженности электрического поля как функцию расстоя-
O |
|
ния r от центра стержня до точки прямой, совпадающей с |
||
|
осью стержня r > a. |
|||
|
l |
Решение. |
||
|
Вводим обозначения: x r a. Выделим на стержне элемент |
|||
dl |
|
|||
|
|
q |
|
|
|
|
dl, заряд этого элемента равен: dq |
dl . Напряженность |
|
|
|
|
||
|
|
|
2a |
|
поля, создаваемого в точке наблюдения таким зарядом равна:
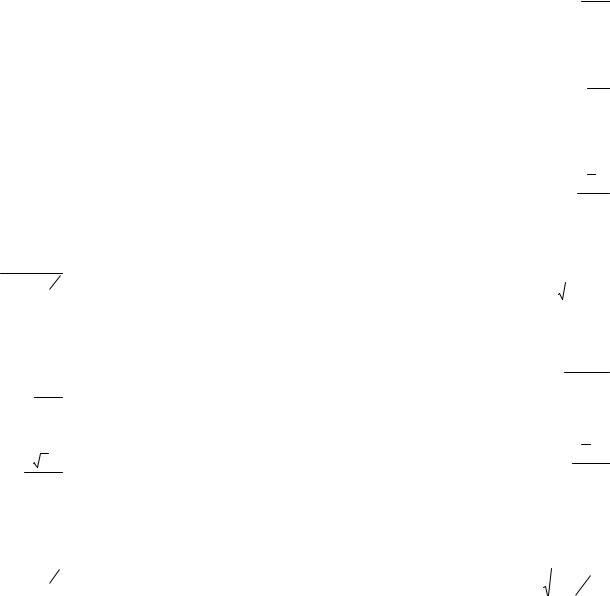
dE |
kdq |
|
kqdl |
, |
x a l 2 |
2a x a l 2 |
где l – расстояние от центра стержня до элемента dl. Поле, создаваемое всем стерж7нем будет равно:
|
|
|
|
|
a |
|
|
kq |
|
|
|
|
|
|
kq |
a |
|
|
|
dl |
|
|
|
||||||
E dE |
|
|
|
|
dl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2a x a l 2 |
|
2a |
|
x a l 2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
y x a l |
|
kq |
x 2a |
|
|
|
|
|
kq 1 x 2a |
|
|
|
|||||||||||||||||
|
|
|
dy |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|x |
|
|
|
|||||||||
dy dl |
2a |
|
y2 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2a y |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kq 1 |
|
|
1 |
|
|
kq |
|
|
|
|
|
|
|
|
|
|
kq |
|
|
kq |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x x 2a |
r a r a 2a |
r |
2 a2 |
||||||||||||||||||||||
|
2a x |
|
x 2a |
|
|
|
|
|
|
||||||||||||||||||||
III. Задачи для самостоятельного решения
1.1. Кольцо радиуса R имеет заряд q. Найти модуль напряженности электрического поля на оси кольца как функцию расстояния L до его центра.
kqL
Ответ: E R2 L2 32 .
1.2. Тонкая проволока, представляющая по форме кольцо радиуса R, заряжена равномерно зарядом q. Найти напряженность поля в центре кольца.
Ответ: E 0 . 1.3. Тонкое полукольцо радиуса R имеет положительный заряд q. Найти напряженность в центре кривизны этого полукольца.
2kq
Ответ: E .
R2
1.4. Тонкая проволока, представляющая по форме три четверти кольца радиуса R, заряжена равномерно зарядом q. Найти напряженность поля в центре кривизны.
2 2kq
Ответ: E . 3 R2
1.5. Тонкое непроводящее кольцо радиуса R заряжено с линейной плотностью
0 cos , где 0 |
const, - азимутальный угол. Найти напряженность: а) в центре |
||||||||
кольца, б) на оси кольца в зависимости от расстояния L. |
|
|
|
|
|
|
|
||
|
|
|
k |
4k |
0 |
R2 |
|
|
|
|
|
Ответ:a)E |
0 |
,б)E |
|
|
|
. |
|
1.6. Тонкое |
|
2R |
R2 L2 3 |
2 |
|||||
|
|
|
|
||||||
непроводящее кольцо радиуса R заряжено с линейной |
плотностью |
||||||||
0 sin , |
где 0 |
const, - азимутальный угол. Найти напряженность в центре |
|||||||
кольца. |
|
|
|
|
|
|
|
|
|
Ответ: E k 0 .
R
1.7. Очень длинная прямая нить заряжена с линейной плотностью . Найти модуль и направление напряженности электрического поля в точке, которая отстоит от нити на расстояние L и находится на перпендикуляре к нити.
Ответ: E 2k .
L
1.8. Очень длинная прямая нить заряжена с линейной плотностью . Найти модуль и направление напряженности электрического поля в точке, которая отстоит от нити на расстояние L и находится на перпендикуляре к нити, проходящем через один из ее концов.
Ответ: E 
 2k .
2k .
L
1.9. Тонкий прямой стержень длины 2а равномерно заряжен с линейной плотностью . Найти E(L), где L -расстояние от центра стержня до точки прямой, перпендикулярной стержню и проходящей через его центр.
Ответ: E |
|
2k a |
|
. |
|
L |
|
|
|
||
|
|
a2 L2 |
|||
1.10. Тонкий прямой стержень длины 2а равномерно заряжен с линейной плотностью. Найти E(L), где L -расстояние от центра стержня до точки прямой совпадающей с осью стержня, если L a .
2k a
Ответ: E .
L2 a2
1.11. Равномерно заряженная нить, на единицу длины которой приходится заряд , имеет конфигурацию, показанную на рис.1.3. Радиус закругления R гораздо меньше длинны нити. Найти модуль напряженности электрического поля в точке О.
Ответ:a)E 0, б)E 
 2 k .
2 k .
R
1.12. Находящаяся в вакууме тонкая пластинка радиуса R равномерно заряжена с поверхностной плотностью . Найти модуль напряженности электрического поля на оси пластинки как функцию расстояния L от ее центра.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Ответ: E |
|
1 |
|
|
|
. |
|||
|
|
|
|
|
|
|
|||
2 |
|
1 R |
|
|
|||||
|
|
0 |
|
L |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
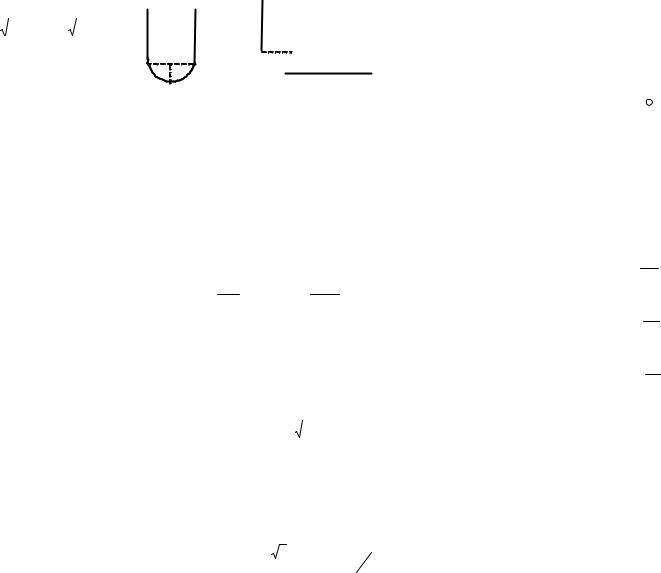
1.13. Плоское кольцо, внутренний радиус которого а, внешний в, заряжено с поверхностной плотностью . Найти модуль напряженности электрического поля на оси кольца как функцию расстояния L от его центра.
|
L |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
||
Ответ: E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
0 |
|
2 |
a |
2 |
2 |
2 |
|
|
|||||
|
|
|
L |
|
|
|
|
L |
b |
|
|
|
|||
1.14. Заряд q распределен равномерно по объему шара радиуса R. Найти потенциал: а) в центре шара 0, б) внутри шара (r), в) вне шара (r), где r - расстояние от центра шара.
О О
О
б
а
Рис.1.3
|
|
|
3q |
|
3q |
|
r2 |
|
q |
|
|
Ответ:a) |
0 |
|
|
, б) |
|
1 |
|
|
,в) |
|
. |
|
|
|
2 |
|
|||||||
|
|
8 0R |
|
8 0R |
|
3R |
|
4 0r |
|
||
|
|
|
|
|
|
|
|
||||
1.15. Потенциал поля внутри заряженного шара ar2 b , где а и b – постоянные.
Найти зависимость объемной плотности заряда (r) от расстояния от центра шара. Ответ: 6 0а .
1.16. По сфере радиуса R равномерно распределены заряды с поверхностной плотностью Найти потенциал в зависимости от расстояния до центра сферы.
Ответ: R ,r R, R2 ,r R .
0 0r
1.17. Плоское кольцо, внутренний радиус которого а, внешний b, заряжено с поверхностной плотностью . Найти потенциал в центре кольца.
Ответ: 2 k b a . 1.18. Находящаяся в вакууме тонкая пластинка радиуса R равномерно заряжена с поверхностной плотностью . Найти потенциал электрического поля на оси пластинки как функцию расстояния L от ее центра.
|
|
|
|
|
|
2 |
|
2 |
|
|
||
|
Ответ: |
|
|
|
|
|
L |
R |
|
L . |
||
|
|
2 0 |
|
|||||||||
1.19. Две |
|
|
|
|
|
|
|
|
||||
длинные одноименно заряженные нити расположены |
|
на |
расстоянии |
|||||||||
d 10см |
друг от друга. Линейная плотность заряда на нитях |
|
|
2 |
10 7 |
Кл |
. |
|||||
|
|
|||||||||||
|
1 |
|
|
|
|
|
|
см |
||||
|
|
|
|
|
|
|
|
|
|
|
||
Найти величину и направление напряженности результирующего электрического поля в точке, находящейся на расстоянии r 10см от каждой нити.
Ответ: E |
2 |
3 k |
31,2 |
кВ |
. |
|
r |
||||
|
|
|
м |
|
§2. Теорема Гаусса
I. Краткие теоретические сведения
Теорема Гаусса: поток вектора E сквозь замкнутую поверхность равен алгебраи-
ческой сумме зарядов внутри этой поверхности, деленной на 0 .
|
|
|
q |
|
EdS |
|
|
. |
|
|
||||
|
|
|
0 |
|
Число задач, легко решаемых с помощью теоремы Гаусса, ограничено. Применять теорему Гаусса эффективно лишь в том случае, когда поле обладает специфической симметрией – плоской, сферической или цилиндрической. В этом случае легко найти достаточно простую замкнутую гауссову поверхность.
Для упрощения математических расчетов во многих случаях истинное распределение точечных дискретных зарядов заменяют непрерывным распределением с некоторой объемной , поверхностной или линейной плотностью.
Объемная плотность заряда:
dq q dV . dV
Поверхностная плотность заряда:
dq q dS . dS
Линейная плотность заряда:
dq q dl . dl
II. Примеры решения задач
Пример 2.1. Найти поле равномерно заряженного по объему зарядовой плотностью бесконечного цилиндра на расстоянии r от его оси. Радиус цилиндра R.
Решение.
Электростатическое поле равномерно заряженного цилиндра имеет радиальный характер: направление вектора E в любой точке перпендикулярно оси цилиндра, а модуль вектора E зависит только от расстояния r до оси цилиндра. (рис.2.1.). Ясно, что при такой конфигурации поля в качестве гауссовой поверхности нужно взять цилиндр радиуса r, ось которого совпадает с осью данного цилиндра (рис. 2.2.). Тогда модуль вектора E на гауссовой поверхности всюду имеет одинаковое значение (данный факт позволяет вынести E за знак интеграла).
Рассмотрим два случая:
1) Если r<R, то поток вектора E сквозь боковую поверхность гауссова цилиндра
примет вид:
 EdS E
EdS E dS ES E2 rh ,
dS ES E2 rh ,
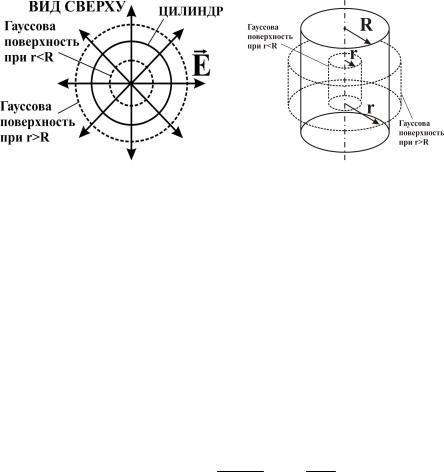
Рис. 2.1 |
Рис. |
|
2.2 |
где S 2 rh - площадь боковой поверхности гауссова цилиндра высотой h. Заряд, заключенный внутри гауссовой поверхности, равен:
q dV dV V 2h,
где V- объем цилиндра, в котором сосредоточен заряд. В данном случае V совпадает с объемом гауссова цилиндра.
|
r2 h |
|
r |
|
E2 rh |
|
E |
|
. |
0 |
|
|||
|
|
2 0 |
||
2) При r>R
q dV dV V .
Теперь V не совпадает с объемом гауссова цилиндра V R2 h
q R2 h.
Тогда :
E2 rh R2 h E R2 .
0 |
2r 0 |
Пример 2.2. Бесконечно длинный цилиндр радиуса R заряжен с объемной плотностьюar , a- постоянная, r- расстояние от оси цилиндра. Найти E(r).
Решение.
Все рассуждения относительно выбора гауссовой поверхности повторяют предыдущую задачу. Поэтому сразу перейдем к рассмотрению двух случаев.
1)При r < R  EdS E2 rh и q dV . Так как объемная плотность является
EdS E2 rh и q dV . Так как объемная плотность является
функцией расстояния r, то нельзя выносить за знак интеграла, как это делалось ранее.
V r2 h dV 2 rhdr .
Тогда
r |
3 |
|
2 ahr3 |
|
ar2 |
|
|
q ar2 rhdr |
2 ahr |
E2 rh |
E |
. |
|||
|
|
3 0 |
|
||||
3 |
|
|
|
3 0 |
|||
0 |
|
|
|
|
|
|
|
2) При r>R
R |
|
2 ahR3 |
|
aR3 |
|
|
q ar2 rhdr |
2 ahR3 |
E2 rh |
E |
. |
||
|
3 0 |
|
||||
3 |
|
|
3r 0 |
|||
0 |
|
|
|
|
|
|
Следует обратить внимание, что интегрирование идет в пределах от 0 до R. В пространстве от R до r заряда нет.
Пример 2.3. На оси бесконечно длинного полого цилиндра радиуса R расположена бесконечная нить, заряженная с линейной плотностью . Пространство за цилиндром заряжено с объемной плотностью 0 r5/3 , 0- постоянная, r- расстояние от оси цилиндра. Найти E(r).
Решение.
Поле обладает цилиндрической симметрией, поэтому выбор гауссовой поверхности очевиден.
1) При r<R существует только электростатическое поле, созданное нитью
|
|
E2 rh |
q |
. |
|||
|
|
|
|||||
|
|
|
|
|
0 |
||
Заряд: q dl h E |
|
|
2k |
|
|||
2 r 0 |
r |
||||||
|
|
||||||
2) При r>R в области существует как поле нити, так и поле, создаваемое заряженной средой. В силу принципа суперпозиции:
E Eнити Есреды .
Заметим, что поле среды также обладает цилиндрической симметрией, поэтому от векторов в принципе суперпозиции можно перейти к модулям:
E Eнити Есреды .
Определим поле среды:
|
1 |
r |
|
|
|
|
3 |
|
0 |
|
r11/ 2 R11/ 2 |
||||
Eсреды 2 rh |
0 r5/ 2 2 rhdr Eсреды |
|
|
||||||||||||
0 |
11 0 |
|
r |
||||||||||||
|
R |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
E |
2k |
|
3 0 r11/ 2 |
|
R11/ 2 |
||||||||
|
|
r |
|
|
|
|
|
|
|
|
|
r |
|
||
|
|
|
11 0 |
|
|
|
|
|
|
||||||
При r поле, создаваемое нитью, стремится к нулю; поле же среды с расстоянием растет, что связано с возрастающей от расстояния объемной плотностью заряда.
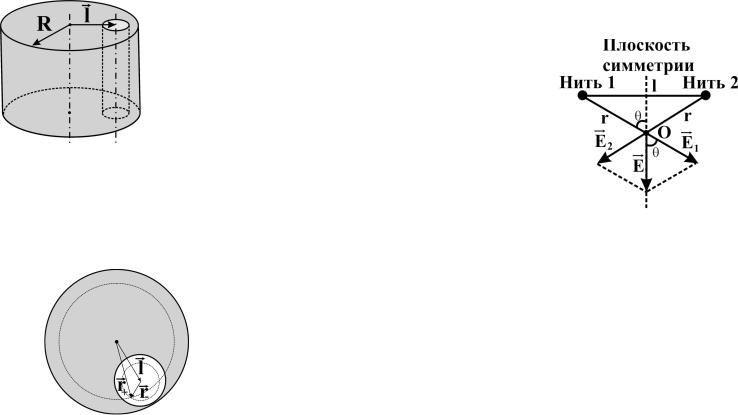
Пример 5.4. Внутри бесконечно длинного равномерно заряженного цилиндра имеется бесконечная цилиндрическая полость (Рис.2.3). Объемная плотность заряда цилиндра. Ось цилиндрической полости параллельна оси цилиндра и смещена относительно
нее на расстояние, характеризуемое вектором l . |
|
|
Найти E внутри полости. |
|
|
Решение. |
|
|
При решении данной задачи пользуются мо- |
|
|
дельным представлением: вместо цилиндра с по- |
|
|
лостью рассматривают равномерно заряженный |
|
|
(для определенности пусть 0) большой ци- |
|
|
линдр и отрицательно заряженный с 0 ци- |
|
|
линдр меньшего радиуса в нем. Такая модель |
|
|
соответствует исходной постановке задачи, так |
|
|
как в области полости отрицательные и положи- |
Рис. 2.3 |
|
тельные заряды компенсируют друг друга, и по- |
||
|
||
зволяет использовать принцип суперпозиции, что |
|
|
значительно упрощает решение задачи. |
|
Определим напряженность поля большого цилиндра в точке, характеризуемой ра- диус-вектором r (рис. 2.4):
E 2 r h |
r2 h |
E |
r |
|
|
||||||||||||
|
|
|
|
2 0 |
|
||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||
Аналогично, |
E |
|
r |
. |
В векторной форме общее |
|
|||||||||||
|
|
|
|||||||||||||||
|
|
|
2 0 |
|
|
|
|
|
|
|
|
|
|
|
|||
поле внутри полости имеет вид: |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
r |
|
|
r |
. |
|
|||||
E E E |
|
|
|
||||||||||||||
|
2 0 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 0 |
|
||||||
Знак «-» появился из-за того, что цилиндр меньшего |
|
||||||||||||||||
диаметра заряжен отрицательно. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
l |
Рис. 2.4 |
||||||||
|
E |
|
|
|
(r r ) |
|
|
. |
|||||||||
|
2 0 |
2 0 |
|
||||||||||||||
Таким, образом, |
поле в полости является однород- |
|
|||||||||||||||
ным, и вектор E направлен параллельно вектору l . Этот вывод справедлив независимо от соотношения радиусов цилиндров и расстояния между их центрами.
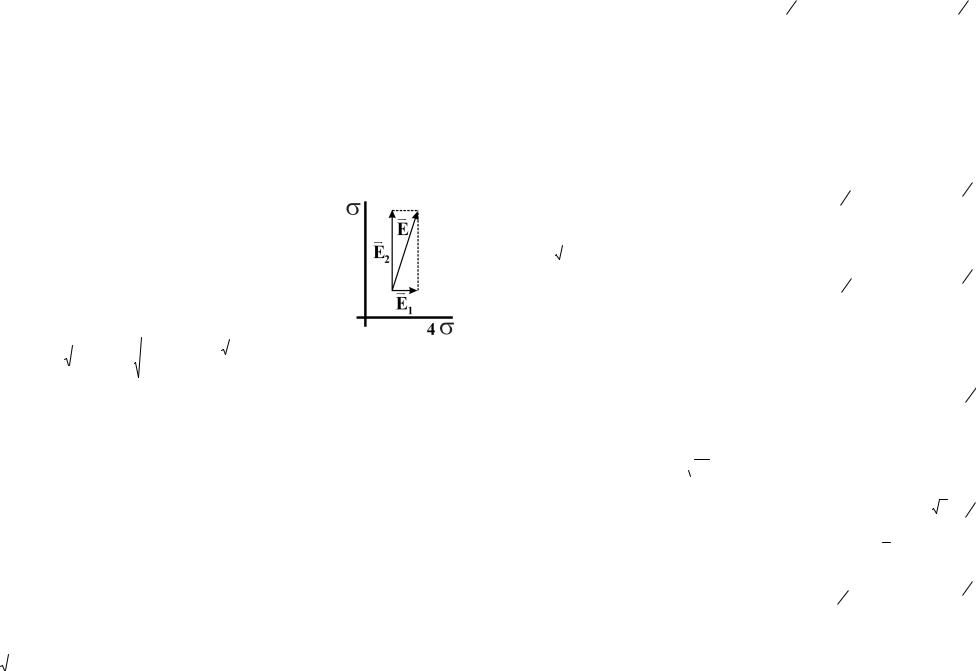
Пример 2.5. Две длинные параллельные нити равномерно заряжены каждая с линейной плотностью . Расстояние между нитями l. Найти максимальное значение модуля напряженности электрического поля в плоскости симметрии этой системы, расположенной между нитями.
Решение.
Модуль вектора напряженности каждой нити легко определить с помощью теоремы Гаусса. Действительно, выбирая в качестве гауссовой поверхности цилиндр, получим:
|
|
|
|
|
|
|
|
E 2 rh |
|
h |
E E |
2 |
|
2k |
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
r |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||
В некоторой точке О (рис. 2.5), лежащей в плоско- |
|
|
|
|
|
|
|
|
||||||||||||||||||||
сти симметрии данной системы, напряженность |
|
|
|
|
|
|
|
|
||||||||||||||||||||
общего электростатического поля нитей определим |
|
|
|
|
|
|
|
|
||||||||||||||||||||
из принципа суперпозиции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
E E1 E2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
или в проекциях на направление вектора E : |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
E E cos E |
2 |
cos 2E cos |
4k |
cos . |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|||||||
|
l |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Так как |
sin r |
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2r |
|
|
|
|
|
2sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
E |
8k sin cos |
. |
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.5 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Найдем максимальное значение | E |: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
dE |
|
8k |
cos2 0 |
|
Emax |
4k |
. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
d |
|
l |
4 |
|
|
|
|
|
l |
|
|
|
|
|||||||||
Пример 2.6. Шар радиуса R имеет положительный заряд, объемная плотность которо- |
||||||||||||||||||||||||||||
го зависит только от расстояния r до его центра как |
|
|
|
r |
, где 0- постоянная. |
|||||||||||||||||||||||
0 1 |
|
|
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|||
Найти: а) модуль напряженности электростатического поля внутри и вне шара как функцию r; б) максимальное значение модуля напряженности Emax и соответствую-
щее ему значение rmax .
Решение.
а) Поле шара является центрально-симметричным: вектор напряженности электростатического поля E направлен по радиус-вектору r и проходит через центр ша-
ра, а модуль вектора E зависит только от расстояния r до центра шара. В качестве гауссовой поверхности необходимо выбрать концентрическую сферу радиуса . Рассмотрим два случая:
1)При r<R найдем поток вектора E сквозь гауссову сферу.
 EdS
EdS  EdS ,
EdS ,
так как E dS .

На гауссовой поверхности | E | const , поэтому E можно вынести за знак интегра-
ла. Следовательно, E dS E4 r2 , где S 4 r2 - площадь гауссовой сферы.
dS E4 r2 , где S 4 r2 - площадь гауссовой сферы.
Найдем заряд q, заключенный внутри гауссовой поверхности:
q dV , V |
|
4 |
r3 dV 4 r2 dr |
, |
|
|||||
3 |
|
|||||||||
r |
r |
|
|
|
4 |
|
r |
4 |
|
|
q 0 (1 |
|
|
|
|
|
|||||
|
)4 r2 dr 0 ( |
|
r3 |
|
|
) |
||||
R |
3 |
R |
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
Подставим полученные значения заряда и потока в формулу теоремы Гаусса:
E4 r2 0 (4 r3 r4 ) E 0 r (1 3r )
2) При r>R |
|
|
0 3 |
|
|
R |
|
3 0 |
4R |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 0 |
R |
r |
|
|
0 R3 |
|
||
|
2 |
|
(1 |
2 |
|
. |
|||||
E4 r |
|
|
|
|
|
)r |
|
dr E |
|
||
|
0 |
R |
|
12 0 r2 |
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
б) Найдем максимальное значение модуля напряженности электростатического поля шара E max . Максимум имеется при r<R, что следует непосредственно из вида
зависимости E(r). Найдем производную d E 0: dr
|
|
0 |
r |
|
|
0 |
r |
2 |
|
dE |
|
0 |
|
|
0 |
r |
|
|
2r |
||
E(r) |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 r |
|
|
, |
||||
3 0 |
4R |
|
|
|
|
2R |
|
||||||||||||||
|
|
|
|
dr |
3 0 |
max |
|
3 0 |
|||||||||||||
Emax 0 .
9R 0
Пример 2.7. Вычислить напряженность электростатического поля равномерно заряженной зарядом q сферы радиуса R.
Решение.
В качестве гауссовой поверхности выбираем сферу радиуса r.
|
|
q |
q |
|
||
1) Пусть r>R. Тогда EdS ES E4 r |
2 |
|
E |
|
|
|
|
4 r |
2 |
0 |
|||
|
|
0 |
|
|||
2) Пусть r<R. В этом случае замкнутая поверхность не содержит внутри зарядов, поэтому в этой области всюду E 0 , т.е. внутри заряженной сферической поверхности электростатическое поле отсутствует.
Пример 2.8. Система состоит из шара радиуса R, заряженного сферически симметрич-
но, и окружающей среды, заполненной зарядом с объемной плотностью a , где a- r
постоянная и r расстояние до центра. Найти заряд шара, при котором модуль напряженности электрического поля вне шара не зависит от r.
Решение.
Так как шар заряжен сферически симметрично, то в качестве гауссовой поверхности выбираем сферу радиуса r.
Пусть искомый заряд шара q. Напряженность электростатического поля при r>R равна сумме: E Eшара Eсреды
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
dV |
|
|
|
a |
4 r2 dr |
|
|
|
|
|
|
||
|
|
|
|
|
|
kq |
|
|
|
|
|
|
|
|
|
a |
|
aR |
2 |
|
||||||
|
|
|
E |
|
|
,E |
|
|
|
|
|
R r |
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
4 r2 0 |
|
|
|
2 0 |
2 0 r2 |
||||||||||||
|
|
|
шара |
|
|
r2 |
среды |
|
|
|
|
4 r2 0 |
|
|
|
|||||||||||
Тогда E |
kq |
|
a |
|
|
aR2 |
|
|
q 2 aR2 |
|
|
|
a |
|
const . |
|
|
|
|
|
|
|||||
r |
2 |
2 0 |
|
2 0 r |
2 |
|
0 4 r2 |
2 0 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Напряженность E не зависит от r при условии, что q 2 aR2 E a . 2 0
Пример 2.9. Найти напряженность электрического поля в области пересечения двух
шаров, равномерно заполненные разноименны- |
|
||||||||||||||||
ми по знаку зарядами с объемной плотностью |
|
||||||||||||||||
( ) и ( ), если расстояние между центрами |
|
||||||||||||||||
шаров характеризуется вектором a . |
|
|
|
||||||||||||||
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|||||
При решении воспользуемся |
принципом |
|
|||||||||||||||
суперпозиции: |
E E E , где |
E |
и E |
- на- |
|
||||||||||||
пряженности полей, создаваемых шарами с |
|
||||||||||||||||
объемными плотностями |
( ) |
|
и |
( ), соот- |
Рис. 2.6 |
||||||||||||
ветственно, |
в |
|
области |
|
|
|
пересечения |
||||||||||
|
|
|
|
|
|||||||||||||
(Рис. 2.6). Легко определить, что |
|
|
|
|
|
|
|||||||||||
|
|
|
|
r |
|
|
|
|
r |
|
, тогда |
|
|
||||
E |
|
|
|
|
,E |
|
|
|
|
|
|||||||
3 0 |
|
3 0 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
a |
|
|
|
|||||||
E |
|
|
|
(r r ) |
|
. |
|
|
|||||||||
|
3 0 |
3 0 |
|
|
|||||||||||||
Таким образом, поле внутри области пересе- |
|
||||||||||||||||
чения двух разноименно заряженных шаров од- |
|
||||||||||||||||
нородно, и вектор напряженности E параллелен |
|
||||||||||||||||
характеристическому вектору a . |
|
|
|
|
|
|
|||||||||||
Пример 2.10. |
Найти |
|
|
напряженность E |
поля |
|
|||||||||||
внутри сферы радиуса R, по которой распределен |
|
||||||||||||||||
заряд с поверхностной плотностью 0 cos , |
Рис. 2.7 |
||||||||||||||||
где 0 - постоянная, |
- |
полярный угол. При ре- |
|
||||||||||||||
шении использовать тот факт, что такое распределение заряда можно представить как результат малого сдвига друг относительно

друга двух равномерно заряженных шаров, заряды которых одинаковы по модулю и противоположны по знаку.
Решение.
Рассмотрим два шара одинакового радиуса R, имеющие равномерно распределенные по объему заряды с плотностью ( ) и ( ). Пусть центры шаров смещены друг
относительно друга на вектор l (Рис. 2.7). В области пересечения шаров поле является однородным, что было показано в предыдущей задаче:
l E .
3 0
При малом смещении шаров, т. е. при малой длине вектора l мы можем перейти к представлению о поверхностной плотности заряда на сфере. Определим толщину заряженного слоя в точках, определяемых углом . Для этого рассмотрим O1 O2 A , по теореме косинусов:
R2 (R a)2 l2 2l(R a)cos ,
где R- радиус шара. Так как по условию R>>a, R>>l
R2 R2 a2 2Ra l2 2lR (1 a) cos . R
При a 0 2Ra 2l Rcos a lcos .
Зная толщину слоя и объемную плотность, получаем, что на единицу площади в этом месте приходится заряд a lcos 0 cos , где 0 l . Таким образом, мы
пришли к выводу, что результат малого сдвига друг относительно друга двух равномерно заряженных шаров приведет к такому же результату, как если бы у нас была сфера с поверхностной плотностью 0 cos .
Напряженность можно представить как E 0 k , где k - орт оси z, от которой от- 3 0
считывается угол .
Пример 2.11. Найти поле плоскости, равномерно заряженной зарядом с поверхностной плотностью
.
Решение.
Из симметрии задачи следует, что вектор E перпендикулярен плоскости. Он направлен от плоскости, если плоскость заряжена положительно, и к плоскости, если ее заряд отрицателен. В симметричных относительно плоскости точках
вектор E одинаков по модулю. Заметив это, по- Рис. 2.8 строим гауссову поверхность в виде цилиндра с площадью оснований S , расположенными сим-
метрично по разные стороны плоскости. Образующие гауссова цилиндра перпендикулярны плоскости (Рис. 2.8).
Тогда поток вектора напряженности электростатического поля плоскости через одно основание цилиндра будет E S , а через оба основания 2E S . Поток через бо-
ковую поверхность равен нулю, т.к. dS |
и E взаимно перпендикулярны. Таким обра- |
||||||||
|
|
|
|
|
|
|
|
||
зом, EdS 2E S . Заряд, содержащийся |
внутри |
гауссова цилиндра, равен: |
|||||||
q S . |
Следовательно, 2E S |
q |
|
|
S |
E |
|
|
. Т.е. напряженность поля |
0 |
0 |
|
|
||||||
|
|
|
|
2 0 |
|||||
бесконечной равномерно заряженной плоскости не зависит от расстояния до нее. Пример 2.12. Бесконечно большая пластина толщиной 2d равномерно заряжена с объ-
емной плотностью 0 x3/2 , 0-
постоянная. Ось x перпендикулярна плоскости пластины, начало координат в середине пластины. Найти напряженность электрического поля как функцию расстояния x.
Решение.
Выберем начало координат в средней плоскости пластинки, а ось x направим перпендикулярно к ней (Рис. 2.9). Тогда, проводя рассужде-
ния, как в предыдущей задаче, рассмотрим два случая: Рис. 2.9
1) При x<d
E2 S dV ,
0
V 2x S dV 2 S dx ,
где V- объем цилиндра, в котором находится заряд. В данном случае V совпадает с объемом гауссова цилиндра.
|
|
1 |
|
x |
|
|
|
|
|
2 0 |
|
|
|
|||||
E |
|
|
0 x |
3/ 2 |
2 Sdx |
x |
5/ 2 |
. |
||||||||||
2 S 0 |
|
5 |
|
|
|
0 |
|
|||||||||||
2) При x>d |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
d |
|
|
|
|
|
2 0 |
|
|
|
|||||
E |
|
|
|
|
0 x |
3/ 2 |
2 Sdx |
|
d |
5/ 2 |
. |
|||||||
|
2 S 0 |
|
|
|
5 |
|
0 |
|
|
|||||||||
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегрирование в этом случае идет в пределах от ( d) до ( d) ; в пределах от ( d)
до ( x) заряда нет, поэтому интеграл обращается в нуль.
Если непрерывно уменьшать толщину пластинки d, одновременно увеличивая плотность электричества 0, чтобы величина 0 d5/ 2 оставалась постоянной, то в пределе получится бесконечная равномерно заряженная плоскость с поверхностной плот-
ностью электричества |
4 |
0 d5/ 2 , а напряженность поля будет определяться фор- |
|||
5 |
|||||
|
|
|
|
||
мулой E |
|
, полученной в предыдущей задаче. |
|||
|
|||||
|
2 0 |
|
|
||
Пример 2.13. Какое поле создавали бы две безграничные плоскости, если бы одна была заряжена с поверхностной плотностью заряда ( ), а другая - (4 ) , и плоскости
были перпендикулярны друг другу?
Решение. Воспользуемся формулой напряженности равномерно за-
ряженной плоскости, полученной в задаче 2.11: E |
|
. |
||||||||||||||||||||||
|
||||||||||||||||||||||||
Тогда напряженности полей плоскостей равны: |
2 0 |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
E |
|
|
|
,E |
|
2 |
. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
1 |
|
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||
Напряженность общего поля определим по теореме Пифа- |
||||||||||||||||||||||||
гора (Рис. 2.10): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 2 |
|
|
|
|
|
|
|
. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|||||||||||
E E2 |
E2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
2 |
|
|
|
|
4 02 |
|
|
02 |
|
|
2 0 |
|
Рис. 2.10 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Это поле является однородным, и вектор напряженности
E составляет некоторый угол с плоскостью одной из пластин. Проведенные расчеты справедливы вдали от линии пересечения пластин.
III. Задачи для самостоятельного решения
2.1 Найти поле равномерно заряженного по объему зарядовой плотностью цилиндра на расстоянии r от его оси. Радиус цилиндра R.
|
|
|
R2 |
||
Ответ: Е |
|
r,r R, |
E |
|
,r R . |
|
|
||||
|
2 0 |
|
2 0r |
||
2.2 Бесконечно длинный цилиндр радиуса R заряжен с объемной плотностью ar , a- постоянная, r- расстояние от оси цилиндра. Найти E(r).
|
|
|
|
|
a |
|
2 |
|
aR3 |
|
|
|
|
|
Ответ: Е |
|
r |
|
,r R, E |
|
,r R . |
|
|
|
6 0 |
|
|
|||||
2.3 |
|
|
|
|
|
|
|
6 0r |
||
Бесконечно длинный цилиндр радиуса R заряжен |
с |
|
объемной |
плотностью |
||||||
|
|
b |
|
, l,b - постоянные, r- расстояние от оси цилиндра. Найти E(r). |
||||||
|
|
|
||||||||
|
r2 l2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||
|
|
|
|
|
|
|
2 l3 r2 l2 |
2 |
|
|
|
|
|
|
|
2 l3 R2 l |
2 |
2 |
|||||||||||
|
|
|
|
|
Ответ: Е |
|
|
|
,r R, E |
|
|
|
|
|
|
|
|
|
|
,r R . |
|||||||||
2.4 |
|
|
|
|
|
3 0r |
|
|
|
3 0r |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Бесконечно |
длинный |
цилиндр |
радиуса |
R |
заряжен |
с |
объемной |
|
плотностью |
||||||||||||||||||||
0 ek r2 |
, 0,k - постоянные, r- расстояние от оси цилиндра. Найти E(r). |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 ekr2 |
|
|
|
|
|
|
1 ekR2 |
||||||||||
|
|
|
|
|
|
|
|
Ответ: |
Е |
|
|
|
|
|
,r |
R, |
E |
|
|
|
|
|
|
,r R . |
|||||
|
|
|
|
|
|
|
|
2k 0r |
|
|
|
|
|
|
|||||||||||||||
2.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2k 0r |
|||||||||||
Бесконечно |
длинный |
цилиндр |
радиуса |
R |
заряжен |
с |
объемной |
|
плотностью |
||||||||||||||||||||
br5/ 2 , |
b - постоянная, |
r - расстояние от оси цилиндра. Найти E(r). |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2b |
|
|
|
|
|
|
|
2b |
9 |
|
|
|
||||||
|
|
|
|
|
|
|
|
Ответ: Е |
7 |
|
|
|
|
|
|
|
R |
2 |
|
|
,r R . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
2 ,r R, |
E |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
9 0 |
|
|
|
|
|
||||||||||||||
2.6 |
|
|
|
|
|
|
|
|
|
|
9 0 |
|
|
|
|
|
|
|
r |
||||||||||
Бесконечно |
длинный |
цилиндр |
радиуса |
R |
заряжен |
с |
объемной |
|
плотностью |
||||||||||||||||||||
a |
|
, a- постоянная, r- расстояние от оси цилиндра. Найти E(r). |
|
|
|
|
|
|
|||||||||||||||||||||
r |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
2a |
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
Ответ: Е |
1 |
|
|
|
|
|
|
|
R |
2 |
|
|
,r R . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
2 ,r R, |
E |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 0 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 0 |
|
|
|
|
|
|
|
|
r |
|||||||||
2.7 На оси бесконечно длинного полого цилиндра радиуса R расположена бесконечная нить, заряженная с линейной плотностью . Пространство за цилиндром заряжено с объемной плотностью 0 r5/3 , 0 - постоянная, r- расстояние от оси цилиндра. Найти E(r).
|
2k |
|
2k |
3 0 |
|
5 |
||
Ответ: Е |
|
,r R, |
E |
|
|
|
r |
3 ,r R. |
|
|
7 0 |
||||||
|
r |
|
r |
|
|
|||
2.8 На оси бесконечно длинного полого цилиндра радиуса R расположена бесконечная нить, заряженная с линейной плотностью . Пространство за цилиндром заряжено с
объемной плотностью a 
 5r , a- постоянная, r- расстояние от оси цилиндра. Най-
5r , a- постоянная, r- расстояние от оси цилиндра. Най-
ти E(r).
|
2k |
|
2k |
2 5a |
1 |
|||
Ответ: Е |
|
,r R, |
E |
|
|
|
r |
2 ,r R . |
|
|
|
||||||
|
r |
|
r |
3 0 |
|
|||
2.9. Шар радиуса R заряжен с объемной плотностью 0 
 r , 0 - постоянная, r - расстояние от центра шара. Найти E(r).
r , 0 - постоянная, r - расстояние от центра шара. Найти E(r).
|
2 0 |
|
|
2 0 |
7 |
|
|
|
3 |
|
|
R 2 |
|||
Ответ: Е |
|
r 2 ,r R, |
E |
|
|
|
,r R . |
7 0 |
7 0 |
|
|||||
|
|
|
|
r2 |
|||
2.10. Шар радиуса R заряжен с объемной плотностью 0 e k r3 |
, 0,k - постоянные, |
||||||
r- расстояние от центра шара. Найти E(r). |
|
|
|
|
|
|
|
Ответ: Е |
|
|
0 |
1 e kr3 |
1 |
,r R, |
|
E |
0 |
|
1 e kR3 |
|
1 |
|
|
|
,r R . |
||||||||||||||||||||||||||||||||||||||
|
3k 0 |
|
|
|
3k 0 |
r2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2.11. Шар радиуса R заряжен с объемной плотностью |
asinkr3 , |
|
a,k - постоянные, |
||||||||||||||||||||||||||||||||||||||||||||||||||||
r- расстояние от центра шара. Найти E(r). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ответ: Е |
a |
|
|
coskr3 |
1 |
1 |
|
,r R, |
E |
|
a |
|
cos kR3 1 |
|
1 |
|
|
|
,r R . |
||||||||||||||||||||||||||||||||||||
|
|
|
r2 |
|
3k 0 |
|
r2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
3k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2.12. Шар радиуса R заряжен с объемной плотностью |
bcos |
kr3 |
, |
|
b,k - постоянные, |
||||||||||||||||||||||||||||||||||||||||||||||||||
R3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
r- расстояние от центра шара. Найти E(r). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
bR |
3 |
|
|
|
kr |
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
bR |
3 |
sin k |
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||
Ответ: Е |
|
|
sin |
|
|
|
|
,r R, |
|
E |
|
|
|
|
,r R. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
3 |
r |
2 |
|
|
|
|
|
|
|
|
|
|
3k |
0 |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
3k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2.13. Шар радиуса R имеет положительный заряд, объемная плотность которого зави- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
сит от расстояния r до центра шара как 0 (1 a |
|
|
), |
|
0,a- |
постоянные. Найти |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
r |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
E(r). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 r 2a |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
3 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
||||||||||||||||||||||
Ответ: Е |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2a R 2 |
|
|
|
R . |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
r |
2 |
|
,r R, |
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,r |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
0 3 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3r |
7 |
|
|
|
|
r |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2.14. Внутри шара радиусом R распределен заряд с объемной плотностью |
|
|
|
a |
|
. |
a |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
- постоянная. Найти E(r). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
5 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R 2 |
|
|
,r R. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Е |
|
|
|
|
r |
2 ,r R, |
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 0 |
|
|
5 0 |
r2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
2.15. Две концентрические сферы с радиусами R1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
и R2 |
( R2 R1) получили заряды Q1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
и Q2 соответственно, которые равномерно распределились по их поверхности. найди-
те выражения для напряженности электростатического поля в точке, удаленной на расстояние r от центра сфер.
Ответ: E 0, |
r R , |
Е |
Q1 |
,R r R |
2 |
, |
E |
Q1 Q2 |
,r R |
2 |
. |
|
|
||||||||||
|
1 |
|
4 0r2 |
1 |
|
|
4 0r2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
2.16. Сфера радиуса R заряжена с поверхностной плотностью const , в центре сфе-
ры находится заряд ( q) . Найти E(r)
|
q |
|
|
|
q |
R2 |
||
Ответ: Е |
|
|
,r R, |
E |
|
|
|
,r R . |
4 0r |
|
|
|
|||||
|
2 |
|
|
4 0r2 |
0r2 |
|||
2.17. Бесконечная плоская плита толщиной 2d равномерно заряжена по объему с плотностью заряда . Вычислите напряженность электростатического поля.
Ответ: Е |
x |
, x d, |
E |
d |
, x d . |
|
|
||||
|
0 |
|
0 |
||
2.18. Бесконечно большая пластина толщиной 2d равномерно заряжена с объемной плотностью 0 x3/ 2 , 0 - постоянная. Ось x перпендикулярна плоскости пласти-
ны, начало координат в середине пластины. Найти напряженность электрического поля как функцию расстояния x.
|
5 |
|
|
|
5 |
|
|
|
Ответ: |
Е |
2 x |
2 |
, x d, |
E |
2 d |
2 |
, x d . |
5 0 |
|
5 0 |
|
|||||
|
|
|
|
|
|
|
||
2.19. Бесконечно большая пластина толщиной 2d равномерно заряжена с объемной
плотностью 0 e |
k x |
l , 0,k,l - постоянные. Ось x перпендикулярна плоскости пла- |
стины, начало координат в середине пластины. Найти напряженность электрического поля как функцию расстояния x.
|
|
l |
|
|
|
k x |
|
|
l |
|
|
k d |
|
|
|
0 |
|
|
l |
|
|
0 |
l |
|
|||
Ответ: |
Е |
|
|
|
1 e |
|
, x d, |
E |
|
|
1 e |
|
, x d . |
k |
|
|
k |
|
|
||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
2.20. Бесконечно большая пластина толщиной 2d равномерно заряжена с объемной плотностью a(1 e b x) , a,b- постоянные. Ось x перпендикулярна плоскости пла-
стины, начало координат в середине пластины. Найти напряженность электрического поля как функцию расстояния x.
|
|
a |
|
1 |
1 |
e bx |
|
|
a |
|
1 |
1 |
e bd |
|
|||
Ответ: |
Е |
|
x |
|
|
|
, x d, |
E |
|
d |
|
|
|
, x d . |
|||
0 |
b |
b |
0 |
b |
b |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
2.21. Какое поле создавали бы две безграничные плоскости, если бы одна была заряжена с поверхностной плотностью заряда ( ), а другая - ( ), и плоскости были перпендикулярны друг другу?
Ответ: Е 
 2 .
2 .
0
2.22. Какое поле создавали бы две безграничные плоскости, если бы одна была заряжена с поверхностной плотностью заряда ( ), а другая - (3 ), и плоскости были параллельны друг другу?
Ответ: Е 
 10 .
10 .
0
2.23. Какое поле создавали бы две безграничные плоскости, если бы одна была заряжена с поверхностной плотностью заряда ( ), а другая - (4 ) , и плоскости были перпендикулярны друг другу?

Ответ: Е 
 17 .
17 .
0
2.24. Какое поле создавали бы две безграничные плоскости, если бы одна была заряжена с поверхностной плотностью заряда ( 2 ), а другая - ( 3 ) , и плоскости были параллельны друг другу?
Ответ: Е 
 13 .
13 .
0
2.25. Какое поле создавали бы две безграничные плоскости, если бы одна была заряжена с поверхностной плотностью заряда ( ), а другая - ( 2 ), и плоскости были перпендикулярны друг другу?
Ответ: Е 
 5 .
5 .
0
2.26. Расстояние между пластинами плоского воздушного конденсатора a значительно меньше размера пластин, поверхностная плотность заряда . Найти напряженность электрического поля E внутри и вне конденсатора.
2
Ответ: Евн 0 , Есн 0. 2.27. Бесконечно плоская плита толщиной T заряжена поверхностным зарядом так, что одна ее половина, например верхняя, заряжена с равномерной плотностью 1 , а дру-
гая – с плотностью 2 . Вычислите напряженность электростатического поля.
Ответ: Е |
1 2 x |
, |
x |
T |
, |
Е |
1 2 T |
, |
x |
T |
. |
|
|
|
|
||||||||
|
0 |
2 |
|
|
2 0 |
2 |
|
||||
2.28. Три плоскопараллельные тонкие пластины, расположенные на малом расстоянии друг от друга, равномерно заряжены. Поверхностные плотности
|
1 |
3 10 |
8 |
Кл |
, |
2 |
5 10 |
8 |
Кл |
, |
3 |
8 10 |
8 |
Кл |
. Найти напряженность поля в точках, |
|
м2 |
|
м2 |
|
м2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
лежащих между пластинами и с внешней стороны. Построить график зависимости напряженности поля от расстояния, выбрав за начало отсчета положение первой пластины.
Е1 |
|
1 |
3 |
2 |
, Е2 |
|
1 |
3 |
|
2 |
, |
|||||
|
|
|
|
|
|
|
|
|
||||||||
2 0 |
2 0 |
|||||||||||||||
Ответ: |
|
|
|
|
|
. |
||||||||||
|
1 |
3 |
2 |
, Е4 |
|
1 |
3 |
2 |
||||||||
Е3 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 0 |
|
|
|
2 0 |
|
|
|
|
|||||
2.29. Внутри шара, заряженного равномерно с объемной плотностью , имеется сферическая полость. Центр полости смещен относительно центра шара на расстояние, характеризуемое вектором a . Найти напряженность электрического поля внутри полости.
|
|
a . |
|
Ответ: Е |
|||
3 0 |
|||
|
|
2.30. Внутри бесконечно длинного равномерно заряженного цилиндра имеется бесконечная цилиндрическая полость. Объемная плотность заряда цилиндра . Ось цилиндрической полости параллельна оси цилиндра и смещена относительно нее на расстоя-
ние, характеризуемое вектором l . Найти E внутри полости.
|
|
|
|
Ответ: Е |
l . |
||
2 0 |
|||
|
|
2.31. Найти напряженность электрического поля в области пересечения двух шаров, равномерно заполненных разноименными по знаку зарядами с объемной плотностью ( ) и ( ), если расстояние между центрами шаров характеризуется вектором a .
|
|
a . |
|
Ответ: Е |
|||
3 0 |
|||
|
|
2.32. Найти напряженность электрического поля в области пересечения двух цилиндров, равномерно заполненных разноименными по знаку зарядами с объемной плотностью ( ) и ( ), если расстояние между центрами шаров характеризуется вектором
a .
|
|
a . |
|
Ответ: Е |
|||
3 0 |
|||
|
|
2.33. Система состоит из шара радиуса R и заряженной среды с объемной плотностью
a , где a- постоянная и r расстояние до центра. Найти заряд шара, при котором r
модуль напряженности не зависит от r.
Ответ: q 2 aR2 , E 1 a . 2 0
2.34. Бесконечно длинный цилиндр круглого сечения заряжен равномерно с поверхностной плотностью . На его оси расположена бесконечная нить, заряженная с линейной плотностью заряда . При каком условии поле вне цилиндра равно нулю?
Ответ: |
|
. |
|
||
|
2 R |
|
2.35. Система состоит из равномерно заряженной сферы радиусом R и окружающей
среды, заполненной зарядом с объемной плотностью a , где a- положительная r
постоянная, r- расстояние от центра сферы. Найти заряд сферы, при котором напряженность E электрического поля вне сферы не будет зависеть от r Чему равно E?
Ответ: q 2 aR2 , E 1 a . 2 0
