Ч А С Т Ь В Т О Р А Я

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Глава шестая Виды случайных величин. Задание дискретной случайной величины

§1. Понятие случайной величины.

Величина, которая в результате испытания принимает одно из возможного множества своих значений (какое именно – заранее не известно), называется случайной величиной.

	Случайная величина (дискретная)	Множество значений
1	Число очков, выпавших при бросании игральной кости.	1, 2, 3 ,4 ,5 ,6
2	Количество бракованных изделий в партии.
3	Число родившихся мальчиков на 100 новорожденных
4	Число вызовов такси за день
5	Число произведенных выстрелов до первого попадания
6	Число дней в наудачу взятом месяце
7

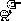
Дискретной называют случайную величину, которая принимает отдельные, изолированные значения с определенными вероятностями.

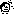Число значений дискретной случайной величины может быть конечным или бесконечным, но счетным.

Непрерывной называют случайную величину, которая принимает, все значения из некоторого конечного или бесконечного промежутка.

	Случайная величина (непрерывная)	Множество значений
1	Вес выбранной наудачу булки	От 100г до 1кг
2	Скорость автомобиля на участке пути
3	Расстояние, которое пролетит пуля при выстреле
4	Расход электроэнергии за год
5

Ч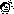исло значений непрерывной случайной величины бесконечно и несчетно.

§2. Закон распределения дискретной случайной величины.

Законом распределения дискретной случайной величины называется соответствие между возможными значениями и их вероятностями.

Закон распределения может быть задан таблицей (рядом распределения), графиком и формулой.

Пусть дискретная случайная величина Х принимает конечное множество значений

с вероятностями соответственно. События(к=1,2,….,n) образуют полную группу, следовательно, .

1	В денежной лотерее из 100 билетов разыгрывается один билет по 50 рублей и 10 билетов по 1 рублю. Найти закон распределения случайной величины – стоимости возможного выигрыша для владельца 1 билета.
	Решение	Вероятность	Ряд распределения	Контроль
		= = =	Х 0 1 50 Р	0,89+0,1+0,01=..
2	Подбрасываются две симметричные монеты, подсчитывается число гербов на обеих верхних сторонах монет. Рассматривается дискретная случайная величина Х- число выпадений гербов на обеих монетах. Найти закон распределения случайной величины
	Решение	Вероятность	Ряд распределения		Контроль
		= = =	Х 0 1 2 Р

3	Два стрелка делают по одному выстрелу в одну мишень. Вероятность попадания для первого стрелка при одном выстреле , для второго -. Рассматривается дискретная случайная величинаХ - число попаданий в мишень. Найти закон распределения случайной величины
	Решение	Вероятность	Ряд распределения	Контроль
	- попадание первого - попадание второго	= = =	Х Р

Ряд распределения может быть изображен графически, если по оси абсцисс откладывать значения случайной величины, а по оси ординат – соответствующие их вероятности. Соединив полученные точки, получим многоугольник распределения.

Дискретная случайная величина Х имеет закон распределения, заданный таблицей. Найдите значение вероятности. Постройте многоугольник распределения.

Х	0,2	0,4	0,6	0,8	1
Р	0,1	0,2	0,4		0,1

Дискретная случайная величина Х имеет закон распределения, заданный в задачах 1-3 . Постройте многоугольник распределения.