
- •Федеральное агентство по образованию
- •Оглавление
- •Тема 1: Линейное программирование. Графическая интерпретация задачи линейного программирования
- •Тема2:. Графический метод решения задач линейного программирования
- •Самостоятельная работа № 1
- •Тема 3: Симплексный метод решения злп
- •Самостоятельная работа № 2
- •Тема 4: Двойственные задачи
- •Самостоятельная работа №3
- •Тема 5: Транспортные задачи
- •Самостоятельная работа № 4.
- •Тема 6: Транспортные задачи с ограничениями по пропускной способности
- •Тема 7: Нелинейное программирование
- •1) При ограничении
- •2) При ограничении.
- •3) При ограничении.
- •4) При ограничении.
- •5) При ограничении.
- •Самостоятельная работа № 5.
- •Тема 8: Теория игр
- •Тема 9. Теория массового обслуживания
- •Лабораторное занятие № 1 Тема: Использование программных комплексов при решении задач линейного программирования
- •Лабораторное занятие №2 Тема: Теория массового обслуживания
- •Домашняя контрольная работа
Самостоятельная работа № 5.
Используя метод множителей Лагранжа, определите глобальный экстремум функции:
В-1: ![]() приx+y=1.
приx+y=1.
В-2: ![]() при
при![]() .
.
В-3: ![]() приx+y=6.
приx+y=6.
В-4: ![]() приx-y=4.
приx-y=4.
В-5: Z=x+y
при
![]()
В-6: ![]() приy-2x=5.
приy-2x=5.
В-7: ![]() при
при![]() .
.
В-8: ![]() при
при![]()
В-9: ![]() при
при![]()
В-10: ![]() при
при![]()
В-11: ![]() при
при![]()
В-12: ![]() при
при![]()
В-13: ![]() при
при![]()
В-14: ![]() при
при![]()
В-15: ![]() при
при![]()
В-16: ![]() при
при![]()
В-17: ![]() при
при![]()
В-18: ![]() при
при![]()
В-19: ![]() при
при![]()
В-20: ![]() при
при![]()
Тема 8: Теория игр
Задание 1
Игра заключается
в том, что игрок А записывает числа 1
(стратегия
![]() ),
или 2 (
),
или 2 (![]() ),
или 3 (
),
или 3 (![]() ).
Игрок В, в свою очередь, может записать
числа 1 (
).
Игрок В, в свою очередь, может записать
числа 1 (![]() ),
или 2 (
),
или 2 (![]() ),
или 3 (
),
или 3 (![]() ),
или 4 (
),
или 4 (![]() ).
Если оба числа окажутся равной четности,
то А выигрывает сумму этих чисел, если
– разной четности, то В выигрывает сумму
этих чисел. Составить платежную матрицу,
определить верхнюю и нижнюю цену игры
и минимаксные стратегии.
).
Если оба числа окажутся равной четности,
то А выигрывает сумму этих чисел, если
– разной четности, то В выигрывает сумму
этих чисел. Составить платежную матрицу,
определить верхнюю и нижнюю цену игры
и минимаксные стратегии.
Решение
Согласно условию, платежная матрица игры имеет следующий вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ:
Задание 2
Для следующих платежных матриц определить нижнюю и верхнюю цены игры, минимаксные стратегии и наличие седловых точек. В последнем случае определить оптимальное решение игры.
а)
 б)
б)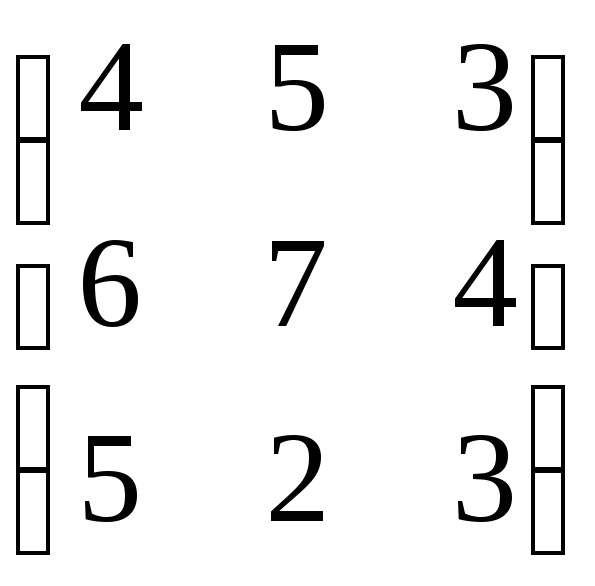
в)
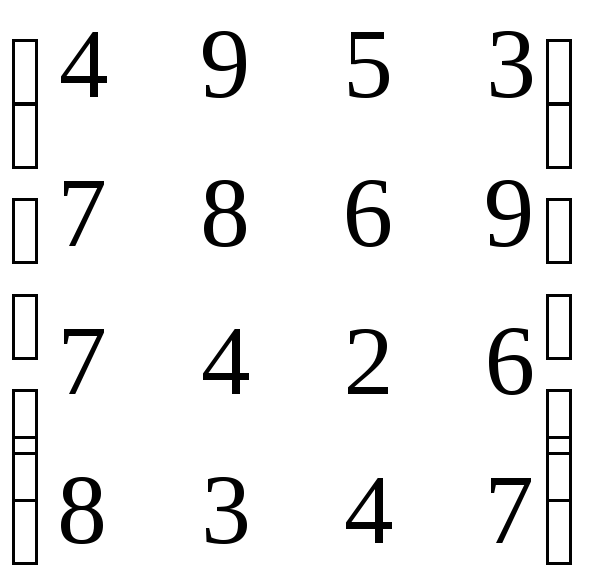 г)
г)
Решение
а) Платежная матрица:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ:
б) Платежная матрица:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ:
в) Платежная матрица:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ:
г) Платежная матрица:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ:
Задание 3
Рассчитать величину платежа для игр, заданных матрицами
а)
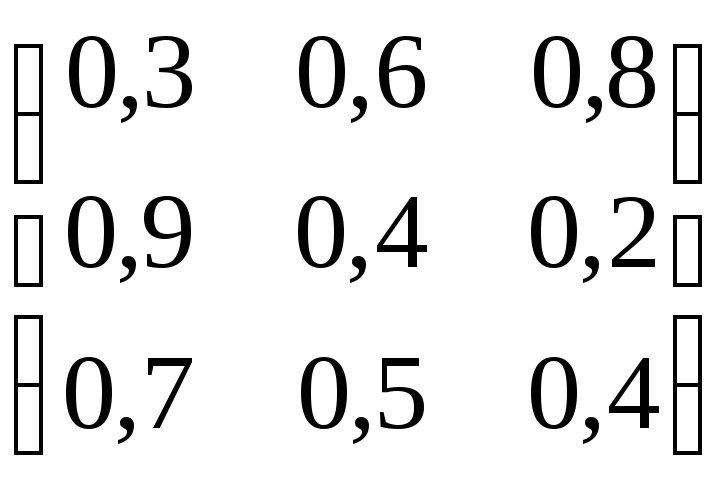 б)
б)
при
![]() и
и![]() .
.
Решение
Задание 4
Привести всевозможные упрощения платежной матрицы в следующих задачах:
а)
 б)
б)
Решение
Задание 5
Решить и привести графическую иллюстрацию игр, заданных следующими матрицами:
а)
![]() б)
б)![]() в)
в)![]() г)
г)![]()
Решение
а) Изобразим графически решение задачи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим систему уравнений:
Ответ:
б) Изобразим графически решение задачи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим систему уравнений:
Ответ:
в) Изобразим графически решение задачи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим систему уравнений:
Ответ:
г) Изобразим графически решение задачи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим систему уравнений:
Ответ:
Задание 6
Найти решение следующих игр:
а)
![]() б)
б)![]() в)
в)![]()
г)
 д)
д) е)
е) ж)
ж)
Решение
а) Изобразим графически решение задачи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим систему уравнений:
Ответ:
б) Изобразим графически решение задачи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим систему уравнений:
Ответ:
в) Изобразим графически решение задачи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим систему уравнений:
Ответ:
г) Изобразим графически решение задачи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим систему уравнений:
Ответ:
д) Изобразим графически решение задачи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим систему уравнений:
Ответ:
е) Изобразим графически решение задачи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим систему уравнений:
Ответ:
ж) Изобразим графически решение задачи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим систему уравнений:
Ответ:
Задание 7
Найти решение и цену игры, заданную матрицей:
а)
 б)
б)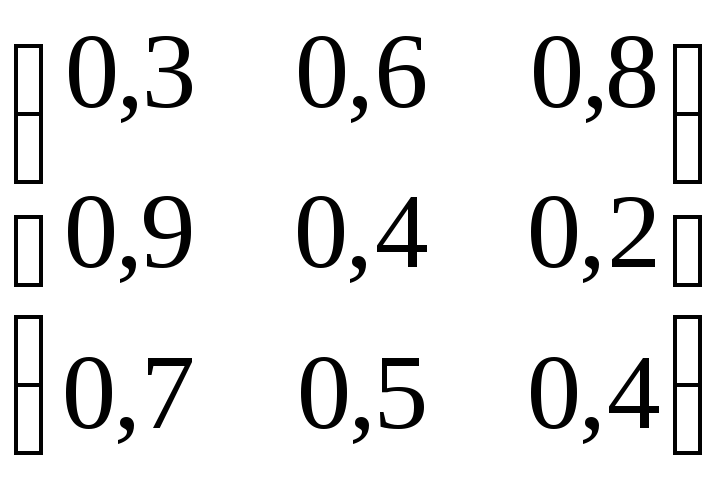 в)
в)
Решение
а) Построим пару двойственных задач:
|
Минимизировать
|
Максимизировать |
Решим симплексным методом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ:
б) Построим пару двойственных задач:
|
Минимизировать
|
Максимизировать |
Решим симплексным методом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ:
в) Построим пару двойственных задач:
|
Минимизировать
|
Максимизировать |
Решим симплексным методом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ:
Задание 2
Построить игру, эквивалентную двойственной паре задач, одна из которых имеет следующий вид:
а)
![]() б)
б)![]()
при
 при
при
в)
![]() б)
б)![]()
при
 при
при

Решение
