Теорема о взаимности перемещений (теорема Максвелла)

На основании теоремы о взаимности работ (9) имеем F₁δ₁₂=F₂δ₂₁, но если принять, чтоF₁=F₂= 1, тогда получаемδ₁₂=δ₂₁, или в общем виде

δ_ij = δ_ji. (10)

«Перемещение точки приложения первой единичной силы по ее направлению, вызванное второй единичной силой, равно перемещению точки приложения второй единичной силы по ее направлению, вызванному первой единичной силой».

Л е к ц и я 9

Определение перемещений. Интеграл мора

Рассмотрим два состояния (рис. 1). Составим выражение работы W₂₁, то есть работы силыF₂= 1 на перемещении Δ₂₁:

W₂₁ = F₂Δ₂₁ = Δ₂₁. (1)

Согласно формулы (7) лекции 8 получаем

W₁₂ = W – W₁₁ – W₂₂, (2)

где

(3)

M, N, Q– это моменты, нормальные и поперечные силы от суммарного действия силF₁иF₂(рис. 7 лекции 8), т.е.

M = M₁ + M₂, N = N₁ + N₂, Q = Q₁ + Q₂. (4)

Значения (4) подставляем в формулу (3), а результат и выражения для W₁₁ иW₂₂– в формулу (2). В итоге получим

(5)

а с учетом равенства (1) имеем

(6)

где черточки показывают, что эти значения возникают от единичных сил.

Формулу (6) можно записать в общем виде:

(7)

Выражение (7) – это формула для определения перемещений в конкретном сечении конструкции или интеграл Мора(формула Мора).

При расчете балок и рам учитывают влияние только изгибающих моментов M, а влияниемNиQпренебрегают.

Правило Верещагина

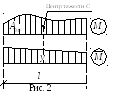«Интеграл произвед ения двух функций, из которых одна линейная, а другая – произвольная, равен площади произвольной функции, умноженной на ординату из прямоугольной функции, лежащей под центром тяжести площади произвольной функции».

Например, имеем две эпюры моментов М_Fи(рис. 2), тогда по формуле (7) получаем при использовании правила Верещагина:

(8)

Запишем еще три положения, вытекающие из правила Верещагина:

1. Ордината у_Сдолжна быть взята из прямолинейной эпюры. Если обе эпюры – прямолинейные, то ординатуу_Сможно брать из любой.

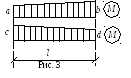
2. Перемножаемые эпюры не должны иметь изломов. При их наличии эпюры необходимо перемножать по участкам.

3. Для перемножения двух прямолинейных эпюр (рис. 3) можно использовать формулу:

Пример.Пусть дана балка, загруженная равномерно распределенной нагрузкойq(рис. 4). Вычислим прогиб балки в точкеСпри ее изгибной жесткостиEI=const. При расчете учитываем только влияние изгибающих моментов, поэтому принимаем интеграл Мора в виде (8):

(9)

где

Вычисляем перемещение Δ_С при помощи интеграла Мора (9):

Вычисляем перемещение Δ_Спри помощи интеграла Мора (9), но с использованием правила перемножения эпюр Верещагина:

Л е к ц и я 10

Определение перемещения сечения стержня плоской статически определимой стержневой системы при действии внешней нагрузки

Данную тему рассмотрим на конкретных примерах.

Пример 1. Определим прогиб конца консоли (рис. 1). Построим грузовую эпюру моментов и эпюру изгибающих моментов от единичной силы, приложенной на конце консоли (рис. 1). Используя правило Верещагина, имеем:

Пример 2.Определим горизонтальное смещение точкиСрамы, изображенной на рис. 2.

A_MF

Построим эпюры изгибающих моментов от внешней нагрузки (М_F) и от силыР= 1, приложенной в точкеСпо направлению искомого горизонтального смещения (), тогда

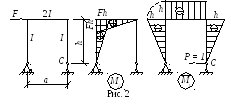
Знак (–) в ответе означает, что горизонтальное смещение точки Си направление единичной силыР= 1 не совпадают.

Пример 3.Определим горизонтальное перемещение точкиВот действия сосредоточенной силыF(рис. 3).

Для криволинейного бруса изгибающий момент в произвольной точке С можно записать в виде:

Если приложить единичную силу в точке Впо направлению действия внешней сосредоточенной силыF(в направлении искомого перемещения), то

и тогда горизонтальное перемещение точки Впри учете только изгибающего момента будет

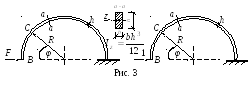
Найдем горизонтальное перемещение точки В при учете только нормальных силN_F, в этом случае

Учтем влияние поперечной силы Q_F на величину горизонтального смещения этой же точкиВ:

Горизонтальное перемещение точки Впри учете изгибающего момента, нормальных и поперечных внутренних сил будет

Если учесть, что для прямоугольного поперечного сечения I_z =bh³/12,А = bh, а также, чтоG= 0,5Е/(1 +ν), то

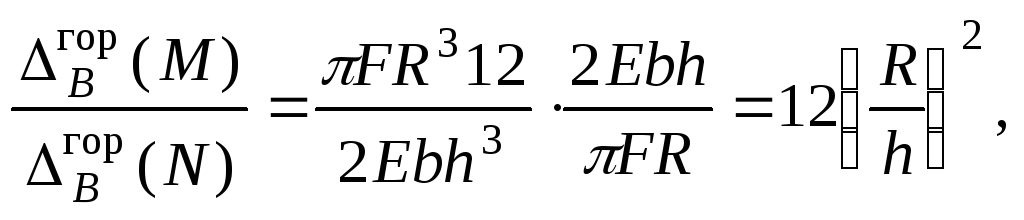
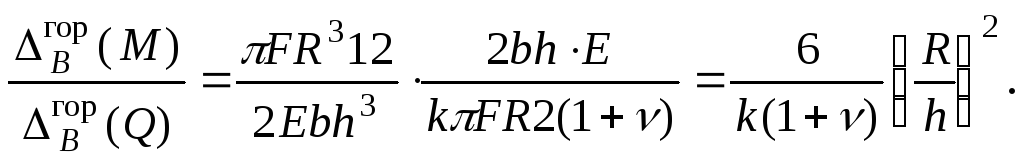
Таким образом, если (R/h) > 1, то при определении горизонтального перемещения влиянием нормальных и поперечных сил можно пренебречь.

Л е к ц и я 11