Построение линий влияния в неразрезных балках

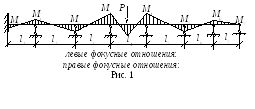Для построения линий влияния нужно, чтобы сила Р= 1 прошла по всем пролетам балки. В определенный момент времени эта единичная сила будет находиться в одном пролете, а все остальные пролеты будут оставаться незагруженными. Если загружен один пролет неразрезной балки, то эпюра моментов имеет вид, показанный на рис. 1.

Введем новые понятия. Абсолютная величина отношения М_n/М_n-1n–го незагруженного пролета при загрузке одного из правых пролетов называетсялевым моментным фокусным отношением n–го пролета, то есть

(1)

Абсолютная величина отношения М_n-1/М_nn–го незагруженного пролета при загрузке одного из левых пролетов называетсяправым моментным фокусным отношением n–го пролета, то есть

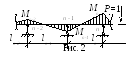
(2)

Рассмотрим два смежных пролета при загрузке одного из правых пролетов (рис. 2). Запишем уравнение трех моментов (7) из лекции 15 для пролетов n– 1 иn:

Разделив полученное уравнение на М_n-1, будем иметь

, или

откуда

(3)

Формула (3) представляет собой рекурентную формулу для определения левого моментного фокусного отношения n–го пролета (k_n), если известно фокусное отношение (n– 1)-го пролета (k_n-1).

Аналогично, рассматривая nиn+ 1 пролеты, можно получить рекурентную формулу для определения правого моментного фокусного отношения

(4)

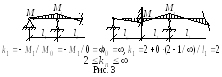На рис. 3 даны примеры определения левых фокусных отношений.

Составим уравнения трех моментов (см. формулу (7) лекции 15) для пролетов n– 1 иnи для пролетовn,n+ 1 (рис. 4):

(5)

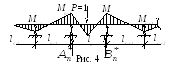Принимая во внимание, что

получим уравнения (5) в виде откуда

(6)

Рассмотрим пролет неразрезной балки, в котором находится единичная сила Р= 1 (рис. 5). Опорные моменты будем находить по формулам (6), где фиктивные опорные реакциииопределим из уравнений равновесия ΣM_n-1= 0 и ΣM_n= 0 в виде

(7)

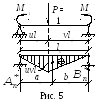Подставляя формулы (7) в выражения для определения опорных моментов (6), получим

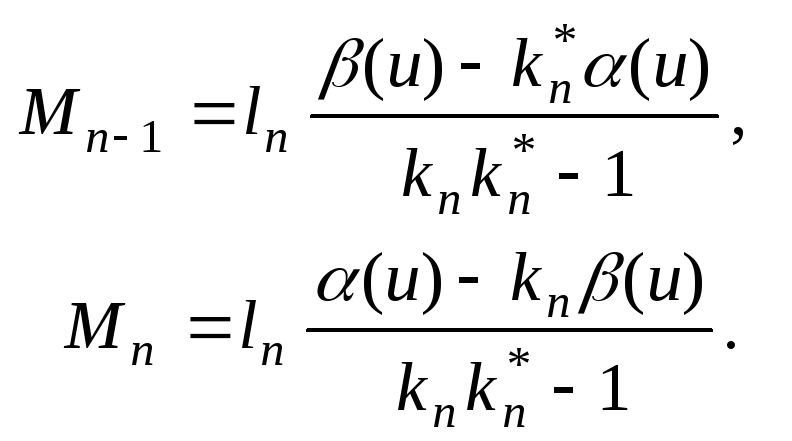(8)

В таблице 1 даны значения α(u) иβ(u) при делении пролета на 10 частей.

Пример.Построить линию влияния опорного моментаМ₂для трехпролетной балки постоянного сечения (рис. 6).

Таблица 1

u	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
α(u)	0,171	0,288	0,357	0,384	0,375	0,336	0,273	0,192	0,099
β(u)	0,099	0,192	0,273	0,336	0,375	0,384	0,357	0,288	0,171

Определим моментные фокусные отношения по формулам (1) и (2) или (3) и (4):

Разбиваем каждый пролет балки на десять частей и составляем расчетную таблицу 2. Таблица составлена следующим образом.

Груз в 1-ом пролете:

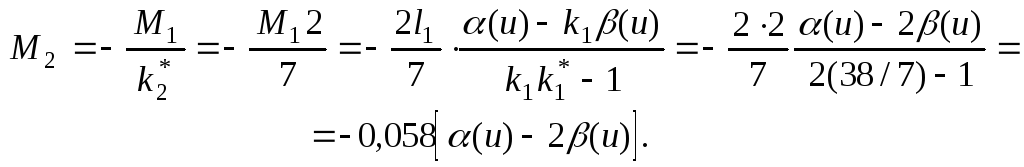
Груз во 2-ом пролете:

Груз в 3-ем пролете:

Груз на консоли:

Опорный момент М₃вычисляется обычным способом. Например, приu= 0,1 имеемM₃= –P·ul= –1·0,1·1= –0,1; приu= 1:M₃= –P·ul= –1·1·1 = –1.

По аналогии строится линия влияния опорного момента М₁(рис. 6,в).

Рассмотрим построение линии влияния изгибающего момента М_хв произвольном сечении второго пролета. Считаем, что линии влиянияМ₁иМ₂уже построены.

Таблица 2

u	Груз в 1-ом пролете: М2 = = –0,058[α(u) – 2β(u)]	Груз во 2-ом пролете: М2 = = 0,464[α(u) – 2,75β(u)]	Груз в 3-м пролете: M2 = –0,717α(u)	Груз на консоли М2 = –0,239М3
0,1 … 0,5 … 1	0,00157 ……. 0,0218 ……. 0,00	-0,047 ……. -0,304 ……. 0,00	-0,123 ……. -0,269 ……. 0,000	0,0239 ……. 0,1196 ……. 0,2390

Рассматривая только часть основной системы в виде простой балки (рис. 6, д), получаем на основании формул (9) лекции 15 приn= 2:

Линия влияния М_хпоказана на рис. 6,е. Она строится наложением трех линий влияния:– линии влияния от внешней нагрузки (Р= 1); линии влиянияМ₁, увеличенной в (4 –х)/4 раз, и линии влиянияМ₂, увеличенной вх/4 раз.

На основании формул (9) лекции 15 при n= 2 имеем

и строим линию влияния поперечной силы в сечении х= сonstвторого пролета (рис. 6,ж).

Линии влияния опорных реакций R_nстроятся по формуле:

(9)

Линия влияния опорной реакции R₂показана на рис. 6,з.

Л е к ц и я 17